A1.5 Statistics

A1.5 Statistics

A1.5.1 Measures of Central Tendency

Measures of central tendency are used to describe, as succinctly as possible, the attributes of a population or a sample from that population. We might use, for example, the average height of the students at a school to represent the entire population. This single number represents some measure of the center point or central tendency of the population. There are several possible measures of central tendency.

A1.5.1.1 Mean.

Because of the very nature of populations in the real world, we will seldom, if ever, have access to the entire population. We will be obliged to work with small sets or samples drawn from the larger population. We will use these samples to draw inferences about measurable aspects of the population called parameters. Before the sample is actually taken from the population, the sample values are considered to be random variables. Thus, if we wish to obtain m sample points from a population induced by a random variable x, then we will have the sample random variables x₁, x₂,...,x_n. The sample mean is also a random variable defined as:

and is an estimator of the population mean. Such functions of random variables are called statistics.

Once a sample is taken we will now have an observation vector x₁,x₂,...,x_n from x₁, x₂,...,x_n. The sample mean will be computed from this sample point as follows:

A1.5.1.2 Median.

The problem with the mean as a measure of central tendency is that it represents the distribution of the mass of the probability distribution. All of the members of a sample might, for example, be tightly clustered together in value, with the exception of one value that is very much larger. This single value would distort our view of where the majority of the mass is actually located. Yet another example of where the mean as a statistic would be misleading would be in the economic arena. Consider, for example, the mean per-capita income in a country like Mexico. This mean is strongly influenced by a small number of individuals who have enormously large incomes in comparison to the near poverty level of most of the citizens. In this case we are more interested in a measure of central tendency that will be more representative of where the per-capita income is located in terms of its frequency or occurrence in the population.

The median of a sample x₁, x₂,...,x_n can be obtained by sorting the observations and then choosing x_M such that . In the special case that nmod2 = 1, we might wish to interpolate such that the median:

Thus, the median as a measure of central tendency has half of the population frequency on either side of the median value.

A1.5.1.3 Mode.

The mode is simply the most frequently occurring value in a sample. If we were to take a sample of students and measure their heights, and find that all of the sample points were different except for three people whose heights were 170 centimeters, then the mode for this sample would be 170. Sometimes in continuous probability distributions we refer to the maximum value in the probability density function as the modal value. In some samples there may be two modal points. In which case the sample distribution is said to be bimodal. In the case were there are several modal values, the distribution will be called multi-modal.

A1.5.2 Measures of Moment

One of the difficulties of the measures of central tendency is that they convey, in most cases, insufficient information as to the actual location of the mass of a distribution in relation to a measure of central tendency. Consider the case of the pdfs shown in Exhibits 1 and 2. In the case of Exhibit 1, most of the mass of the distribution is concentrated right around the mean. In the case of the distribution represented in Exhibit 2, the mass is much less centrally located. Now consider the pdfs represented in Exhibits 3 and 4. In Exhibit 3, we see that the mass is not symmetrically distributed about the mean. In the example of Exhibit 4, the mass is evenly distributed about the mean but is bimodal: the mass of the distribution is concentrated in two nodes that are separated from the mean. To capture these characteristics of probability distributions, we will need additional statistics.

Exhibit 1: Distribution Concentrated near the Mean

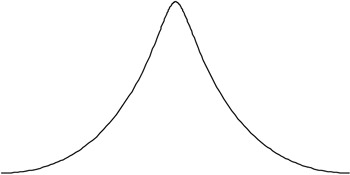
Exhibit 2: Distribution Less Centrally Located

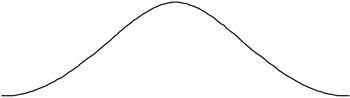
Exhibit 3: Mass not Symmetrically Distributed about the Mean

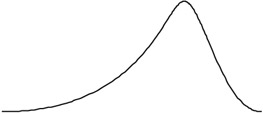
Exhibit 4: Bimodal Distribution

A1.5.2.1 Variance.

Each observation x_i in a sample x₁, x₂,...,x_n will differ from the mean by an amount called the mean deviation. With these mean deviations we can construct a set of moments about the mean. Let M(x,r) represent the r^th moment about the mean. Then:

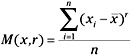
The first moment about the mean, of course, will be zero in that:

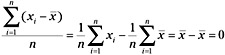
The second moment about the mean is the sample variance:

In that the sample variance tends to be rather large, the sample standard deviation is sometimes used in its stead, as follows:

If a distribution is not symmetrical, the mode may be to the left or right of the mean and either close to the mean or relatively far from it. This will represent the skewness of the distribution. We can compute a coefficient of skewness c_s as follows:

where s is the sample standard deviation defined above. If c_s is negative, then the modal point will lie to the left of the mean; the magnitude of c_s is a measure of this distance. Similarly, if c_s is positive, then the modal point will lie to the right of the mean. Again, the magnitude of c_s is a measure of this distance.

The degree to which a distribution is flattened (see also Exhibit 4) can be assessed by a measure of kurtosis c_k, which is defined as follows:

In this case, if there is a tendency toward bimodality (platykurtic), then c_k > 1. If, on the other hand, c_k < 1, the distribution of the mass of the distribution is very close to the mean (leptokurtic).

A1.5.2.2 Standard Error of the Mean.

Another measure of variation that is very important to us relates to the variation in , the estimate of the population mean. Returning, for a moment, to the sample random variables x₁,x₂,...,x_n, the variance of:

is:

Observe that each of the random variables x_i has the same distribution as x; therefore:

Var(x_i) = Var(x) = σ²

Thus:

The standard deviation of , using the sample estimate s² for σ², is known as the standard error of the estimate of the mean and is defined as:

In general, we can see from this relationship that as the sample size increases, the standard error of the estimate for the mean will decrease.