Examples
The following examples illustrate some of the capabilities of the GENMOD procedure. These are not intended to represent definitive analyses of the data sets presented here. You should refer to the texts cited in the References section on page 1728 for guidance on complete analysis of data using generalized linear models.
Example 31.1. Logistic Regression
In an experiment comparing the effects of five different drugs, each drug is tested on a number of different subjects. The outcome of each experiment is the presence or absence of a positive response in a subject. The following artificial data represent the number of responses r in the n subjects for the five different drugs, labeled A through E. The response is measured for different levels of a continuous covariate x for each drug. The drug type and the continuous covariate x are explanatory variables in this experiment. The number of responses r is modeled as a binomial random variable for each combination of the explanatory variable values, with the binomial number of trials parameter equal to the number of subjects n and the binomial probability equal to the probability of a response.
The following DATA step creates the data set.
data drug; input drug$ x r n @@; datalines; A .1 1 10 A .23 2 12 A .67 1 9 B .2 3 13 B .3 4 15 B .45 5 16 B .78 5 13 C .04 0 10 C .15 0 11 C .56 1 12 C .7 2 12 D .34 5 10 D .6 5 9 D .7 8 10 E .2 12 20 E .34 15 20 E .56 13 15 E .8 17 20 ; run;
A logistic regression for these data is a generalized linear model with response equal to the binomial proportion r/n . The probability distribution is binomial, and the link function is logit. For these data, drug and x are explanatory variables. The probit and the complementary log-log link functions are also appropriate for binomial data.
PROC GENMOD performs a logistic regression on the data in the following SAS statements:
proc genmod data=drug; class drug; model r/n = x drug / dist = bin link = logit lrci; run;
Since these data are binomial, you use the events/trials syntax to specify the response in the MODEL statement. Profile likelihood confidence intervals for the regression parameters are computed using the LRCI option.
General model and data information is produced in Output 31.1.1.
| |
The GENMOD Procedure Model Information Data Set WORK.DRUG Distribution Binomial Link Function Logit Response Variable (Events) r Response Variable (Trials) n
| |
The five levels of the CLASS variable DRUG are displayed in Output 31.1.2.
| |
Class Level Information Class Levels Values drug 5 A B C D E
| |
| |
Criteria For Assessing Goodness Of Fit Criterion DF Value Value/DF Deviance 12 5.2751 0.4396 Scaled Deviance 12 5.2751 0.4396 Pearson Chi-Square 12 4.5133 0.3761 Scaled Pearson X2 12 4.5133 0.3761 Log Likelihood 114.7732 | |
In the Analysis Of Parameter Estimates table displayed in Output 31.1.4, chi-square values for the explanatory variables indicate that the parameter values other than the intercept term are all significant. The scale parameter is set to 1 for the binomial distribution. When you perform an overdispersion analysis, the value of the overdispersion parameter is indicated here. See the the section Overdispersion on page 1659 for a discussion of overdispersion.
| |
Analysis Of Parameter Estimates Likelihood Ratio Standard 95% Confidence Chi- Parameter DF Estimate Error Limits Square Pr > ChiSq Intercept 1 0.2792 0.4196 0.5336 1.1190 0.44 0.5057 x 1 1.9794 0.7660 0.5038 3.5206 6.68 0.0098 drug A 1 2.8955 0.6092 4.2280 1.7909 22.59 <.0001 drug B 1 2.0162 0.4052 2.8375 1.2435 24.76 <.0001 drug C 1 3.7952 0.6655 5.3111 2.6261 32.53 <.0001 drug D 1 0.8548 0.4838 1.8072 0.1028 3.12 0.0773 drug E 0 0.0000 0.0000 0.0000 0.0000 . . Scale 0 1.0000 0.0000 1.0000 1.0000 NOTE: The scale parameter was held fixed.
| |
The preceding table contains the profile likelihood confidence intervals for the explanatory variable parameters requested with the LRCI option. Wald confidence intervals are displayed by default. Profile likelihood confidence intervals are considered to be more accurate than Wald intervals (refer to Aitkin et al. 1989), especially with small sample sizes. You can specify the confidence coefficient with the ALPHA= option in the MODEL statement. The default value of 0.05, corresponding to 95% confidence limits, is used here. See the section Confidence Intervals for Parameters on page 1666 for a discussion of profile likelihood confidence intervals.
Example 31.2. Normal Regression, Log Link
Consider the following data, where x is an explanatory variable, and y is the response variable. It appears that y varies nonlinearly with x and that the variance is approximately constant. A normal distribution with a log link function is chosen to model these data; that is, log( ¼ i ) = x i ² ² so that ¼ i = exp( x i ² ² ).
data nor; input x y; datalines; 0 5 0 7 0 9 1 7 1 10 1 8 2 11 2 9 3 16 3 13 3 14 4 25 4 24 5 34 5 32 5 30 ; run;
The following SAS statements produce the analysis with the normal distribution and log link:
proc genmod data=nor; model y = x / dist = normal link = log; output out = Residuals pred = Pred resraw = Resraw reschi = Reschi resdev = Resdev stdreschi = Stdreschi stdresdev = Stdresdev reslik = Reslik; run;
The OUTPUT statement is specified to produce a data set that contains predicted values and residuals for each observation. This data set can be useful for further analysis, such as residual plotting.
The output from these statements is displayed in Output 31.2.1.
| |
The GENMOD Procedure Model Information Data Set WORK.NOR Distribution Normal Link Function Log Dependent Variable y Criteria For Assessing Goodness Of Fit Criterion DF Value Value/DF Deviance 14 52.3000 3.7357 Scaled Deviance 14 16.0000 1.1429 Pearson Chi-Square 14 52.3000 3.7357 Scaled Pearson X2 14 16.0000 1.1429 Log Likelihood 32.1783 Analysis Of Parameter Estimates Standard Wald 95% Chi- Parameter DF Estimate Error Confidence Limits Square Pr > ChiSq Intercept 1 1.7214 0.0894 1.5461 1.8966 370.76 <.0001 x 1 0.3496 0.0206 0.3091 0.3901 286.64 <.0001 Scale 1 1.8080 0.3196 1.2786 2.5566 NOTE: The scale parameter was estimated by maximum likelihood. | |
The PROC GENMOD scale parameter, in the case of the normal distribution, is the standard deviation. By default, the scale parameter is estimated by maximum likelihood. You can specify a fixed standard deviation by using the NOSCALE and SCALE= options in the MODEL statement.
The data set of predicted values and residuals ( Output 31.2.2) is created by the OUTPUT statement. With this data set, you can construct residual plots using the GPLOT procedure to aid in assessing model fit. Note that raw, Pearson, and deviance residuals are equal in this example. This is a characteristic of the normal distribution and is not true in general for other distributions.
| |
Obs x y Pred Reschi Resdev Resraw Stdreschi Stdresdev Reslik 1 0 5 5.5921 0.59212 0.59212 0.59212 -0.34036 0.34036 0.34036 2 0 7 5.5921 1.40788 1.40788 1.40788 0.80928 0.80928 0.80928 3 0 9 5.5921 3.40788 3.40788 3.40788 1.95892 1.95892 1.95892 4 1 7 7.9324 0.93243 0.93243 0.93243 0.54093 0.54093 0.54093 5 110 7.9324 2.06757 2.06757 2.06757 1.19947 1.19947 1.19947 6 1 8 7.9324 0.06757 0.06757 0.06757 0.03920 0.03920 0.03920 7 211 11.2522 0.25217 0.25217 0.25217 0.14686 0.14686 0.14686 8 2 9 11.2522 2.25217 2.25217 2.25217 1.31166 1.31166 1.31166 9 316 15.9612 0.03878 0.03878 0.03878 0.02249 0.02249 0.02249 10 313 15.9612 2.96122 2.96122 2.96122 1.71738 1.71738 1.71738 11 314 15.9612 1.96122 1.96122 1.96122 1.13743 1.13743 1.13743 12 425 22.6410 2.35897 2.35897 2.35897 1.37252 1.37252 1.37252 13 424 22.6410 1.35897 1.35897 1.35897 0.79069 0.79069 0.79069 14 534 32.1163 1.88366 1.88366 1.88366 1.22914 1.22914 1.22914 15 532 32.1163 0.11634 0.11634 0.11634 0.07592 0.07592 0.07592 16 530 32.1163 2.11634 2.11634 2.11634 1.38098 1.38098 1.38098
| |
Example 31.3. Gamma Distribution Applied to Life Data
Life data are sometimes modeled with the gamma distribution. Although PROC GENMOD does not analyze censored data or provide other useful lifetime distributions such as the Weibull or lognormal, it can be used for modeling complete (uncensored) data with the gamma distribution, and it can provide a statistical test for the exponential distribution against other gamma distribution alternatives. Refer to Lawless (1982) or Nelson (1982) for applications of the gamma distribution to life data.
The following data represent failure times of machine parts , some of which are manufactured by manufacturer A and some by manufacturer B.
data A; input lifetime@@ ; mfg = 'A'; datalines; 620 470 260 89 388 242 103 100 39 460 284 1285 218 393 106 158 152 477 403 103 69 158 818 947 399 127 432 12 134 660 548 381 203 871 193 531 317 85 1410250 41 1101 32 421 32 343 376 1512 179 247 95 76 515 72 1585 253 6 860 89 1055 537 101 385 176 11 565 164 16 1267 352 160 195 1279 356 751 500 803 560 151 24 689 1119 1733 2194 763 555 14 45 776 1 ; data B; input lifetime@@ ; mfg = 'B'; datalines; 1747 945 12 1453 14 150 20 41 35 69 195 89 1090 1868 294 96 618 44 142 892 1307 310 230 30 403 860 23 406 10541935 561 348 130 13 230 250 317 304 79 1793 536 12 9 256 201 733 510 660 122 27 273 1231 182 289 667 761 1096 43 44 87 405 998 1409 61 278 407 113 25 940 28 848 41 646 575 219 303 304 38 195 1061 174 377 388 10 246 323 198 234 39 308 55 729 813 1216 1618539 6 1566 459 946 764 794 35 181 147 116 141 19 380 609 546 ; data lifdat; set A B; run;
The following SAS statements use PROC GENMOD to compute Type 3 statistics to test for differences between the two manufacturers in machine part life. Type 3 statistics are identical to Type 1 statistics in this case, since there is only one effect in the model. The log link function is selected to ensure that the mean is positive.
proc genmod data = lifdat; class mfg; model lifetime = mfg / dist=gamma link=log type3; run;
The output from these statements is displayed in Output 31.3.1.
| |
The GENMOD Procedure Model Information Data Set WORK.LIFDAT Distribution Gamma Link Function Log Dependent Variable lifetime Class Level Information Class Levels Values mfg 2 A B Criteria For Assessing Goodness Of Fit Criterion DF Value Value/DF Deviance 199 287.0591 1.4425 Scaled Deviance 199 237.5335 1.1936 Pearson Chi-Square 199 211.6870 1.0638 Scaled Pearson X2 199 175.1652 0.8802 Log Likelihood 1432.4177 Analysis Of Parameter Estimates Standard Wald 95% Chi- Parameter DF Estimate Error Confidence Limits Square Pr > ChiSq Intercept 1 6.1302 0.1043 5.9257 6.3347 3451.61 <.0001 mfg A 1 0.0199 0.1559 -0.2857 0.3255 0.02 0.8985 mfg B 0 0.0000 0.0000 0.0000 0.0000 . . Scale 1 0.8275 0.0714 0.6987 0.9800 NOTE: The scale parameter was estimated by maximum likelihood. LR Statistics For Type 3 Analysis Chi- Source DF Square Pr > ChiSq mfg 1 0.02 0.8985 | |
The p -value of 0.8985 for the chi-square statistic in the Type 3 table indicates that there is no significant difference in the part life for the two manufacturers.
Using the following statements, you can refit the model without using the manufacturer as an effect. The LRCI option in the MODEL statement is specified to compute profile likelihood confidence intervals for the mean life and scale parameters.
proc genmod data = lifdat; model lifetime = / dist=gamma link=log lrci; run;
| |
The GENMOD Procedure Analysis Of Parameter Estimates Likelihood Ratio Standard 95% Confidence Chi Parameter DF Estimate Error Limits Square Pr > ChiSq Intercept 1 6.1391 0.0775 5.9904 6.2956 6268.10 <.0001 Scale 1 0.8274 0.0714 0.6959 0.9762 NOTE: The scale parameter was estimated by maximum likelihood. | |
The intercept is the estimated log mean of the fitted gamma distribution, so that the mean life of the parts is
The SCALE parameter used in PROC GENMOD is the inverse of the gamma dispersion parameter, and it is sometimes called the gamma index parameter . See the Response Probability Distributions section on page 1650 for the definition of the gamma probability density function. A value of 1 for the index parameter corresponds to the exponential distribution . The estimated value of the scale parameter is 0.8274. The 95% profile likelihood confidence interval for the scale parameter is (0.6959, 0.9762), which does not contain 1. The hypothesis of an exponential distribution for the data is, therefore, rejected at the 0.05 level. A confidence interval for the mean life is
Example 31.4. Ordinal Model for Multinomial Data
This example illustrates how you can use the GENMOD procedure to fit a model to data measured on an ordinal scale. The following statements create a SAS data set called icecream . The data set contains the results of a hypothetical taste test of three brands of ice cream. The three brands are rated for taste on a five point scale from very good (vg) to very bad (vb). An analysis is performed to assess the differences in the ratings for the three brands. The variable taste contains the ratings and brand contains the brands tested. The variable count contains the number of testers rating each brand in each category.
The following statements create the icecream data set.
data icecream; input count brand$ taste$; datalines; 70 ice1 vg 71 ice1 g 151 ice1 m 30 ice1 b 46 ice1 vb 20 ice2 vg 36 ice2 g 130 ice2 m 74 ice2 b 70 ice2 vb 50 ice3 vg 55 ice3 g 140 ice3 m 52 ice3 b 50 ice3 vb ; run;
The following statements fit a cumulative logit model to the ordinal data with the variable taste as the response and the variable brand as a covariate. The variable count is used as a FREQ variable.
proc genmod rorder=data; freq count; class brand; model taste = brand / dist=multinomial link=cumlogit aggregate=brand type1; estimate 'LogOR12' brand 1 1 / exp; estimate 'LogOR13' brand 1 0 1 / exp; estimate 'LogOR23' brand 0 1 1 / exp; run;
The AGGREGATE=BRAND option in the MODEL statement specifies the variable brand as defining multinomial populations for computing deviances and Pearson chi-squares. The RORDER=DATA option specifies that the taste variable levels be ordered by their order of appearance in the input data set, that is, from very good (vg) to very bad (vb). By default, the response is sorted in increasing ASCII order. Always check the Response Profiles table to verify that response levels are appropriately ordered. The TYPE1 option requests a Type 1 test for the significance of the covariate brand .
If ³ j ( x ) = Pr(taste ‰ j ) is the cumulative probability of the j th or lower taste category, then the odds ratio comparing x 1 to x 2 is as follows :
Refer to McCullagh and Nelder (1989, Chapter 5) for details on the cumulative logit model. The ESTIMATE statements compute log odds ratios comparing each of brands. The EXP option in the ESTIMATE statements exponentiates the log odds ratios to form odds ratio estimates. Standard errors and confidence intervals are also computed.
| |
The GENMOD Procedure Model Information Data Set WORK.ICECREAM Distribution Multinomial Link Function Cumulative Logit Dependent Variable taste Frequency Weight Variable count Class Level Information Class Levels Values brand 3 ice1 ice2 ice3 Response Profile Ordered Total Value taste Frequency 1 vg 140 2 g 162 3 m 421 4 b 156 5 vb 166
| |
Output 31.4.2 displays estimates of the intercept terms and covariates and associated statistics. The intercept terms correspond to the four cumulative logits defined on the taste categories in the order shown in Output 31.4.1.That is, Intercept1 is the intercept for the first cumulative logit, ![]() Intercept2 is the intercept for the second cumulative logit
Intercept2 is the intercept for the second cumulative logit ![]() and so forth.
and so forth.
| |
Analysis Of Parameter Estimates Standard Wald 95% Confidence Chi- Parameter DF Estimate Error Limits Square Intercept1 1 1.8578 0.1219 2.0967 1.6189 232.35 Intercept2 1 0.8646 0.1056 1.0716 Z0.6576 67.02 Intercept3 1 0.9231 0.1060 0.7154 1.1308 75.87 Intercept4 1 1.8078 0.1191 1.5743 2.0413 230.32 brand ice1 1 0.3847 0.1370 0.1162 0.6532 7.89 brand ice2 1 0.6457 0.1397 0.9196 0.3719 21.36 brand ice3 0 0.0000 0.0000 0.0000 0.0000 . Scale 0 1.0000 0.0000 1.0000 1.0000 Analysis Of Parameter Estimates Parameter Pr > ChiSq Intercept1 <.0001 Intercept2 <.0001 Intercept3 <.0001 Intercept4 <.0001 brand ice1 0.0050 brand ice2 <.0001 brand ice3 . Scale NOTE: The scale parameter was held fixed.
| |
| |
LR Statistics For Type 1 Analysis Chi Source Deviance DF Square Pr > ChiSq Intercepts 65.9576 brand 9.8654 2 56.09 <.0001 Contrast Estimate Results Standard Chi Label Estimate Error Alpha Confidence Limits Square Pr > ChiSq LogOR12 1.0305 0.1401 0.05 0.7559 1.3050 54.11 <.0001 Exp(LogOR12) 2.8024 0.3926 0.05 2.1295 3.6878 LogOR13 0.3847 0.1370 0.05 0.1162 0.6532 7.89 0.0050 Exp(LogOR13) 1.4692 0.2013 0.05 1.1233 1.9217 LogOR23 0.6457 0.1397 0.05 0.9196 0.3719 21.36 <.0001 Exp(LogOR23) 0.5243 0.0733 0.05 0.3987 0.6894
| |
Example 31.5. GEE for Binary Data with Logit Link Function
Table 31.5 . Respiratory Disorder Data
Patients in each of two centers are randomly assigned to groups receiving the active treatment or a placebo. During treatment, respiratory status (coded here as 0=poor, 1=good) is determined for each of four visits . The variables center , treatment , sex , and baseline (baseline respiratory status) are classification variables with two levels. The variable age (age at time of entry into the study) is a continuous variable.
Explanatory variables in the model are Intercept ( x ij 1 ), treatment ( x ij 2 ), center ( x ij 3 ), sex ( x ij 4 ), age ( x ij 6 ), and baseline ( x ij 6 ), so that ![]() is the vector of explanatory variables. Indicator variables for the classification explanatory variables can be automatically generated by listing them in the CLASS statement in PROC GENMOD. However, in order to be consistent with the analysis in Stokes, Davis, and Koch (1995), the four classification explanatory variables are coded as follows:
is the vector of explanatory variables. Indicator variables for the classification explanatory variables can be automatically generated by listing them in the CLASS statement in PROC GENMOD. However, in order to be consistent with the analysis in Stokes, Davis, and Koch (1995), the four classification explanatory variables are coded as follows:
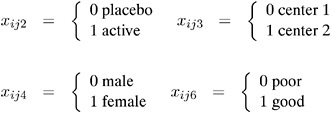
Suppose y ij represents the respiratory status of patient i at the j th visit, j = 1,..., 4, and ¼ ij = E( y ij ) represents the mean of the respiratory status. Since the response data are binary, you can use the variance function for the binomial distribution v ( ¼ ij ) = ¼ ij (1 ˆ’ ¼ ij ) and the logit link function g ( ¼ ij ) = log( ¼ ij / (1 ˆ’ ¼ ij )). The model for the mean is g ( ¼ ij ) = x ij ² ² , where ² is a vector of regression parameters to be estimated.
Further manipulation of the data set creates an observation for each visit with the respiratory status at each visit represented by the binary variable outcome and indicator variables for treatment ( active ), center ( center2 ), and sex ( female ). A partial listing of the resulting data set is shown in Output 31.5.1.
| |
Obs center id age baseline active center2 female visit outcome 1 1 1 46 0 0 0 0 1 0 2 1 1 46 0 0 0 0 2 0 3 1 1 46 0 0 0 0 3 0 4 1 1 46 0 0 0 0 4 0 5 1 2 28 0 0 0 0 1 0 6 1 2 28 0 0 0 0 2 0 7 1 2 28 0 0 0 0 3 0 8 1 2 28 0 0 0 0 4 0 9 1 3 23 1 1 0 0 1 1 10 1 3 23 1 1 0 0 2 1 11 1 3 23 1 1 0 0 3 1 12 1 3 23 1 1 0 0 4 1 13 1 4 44 1 0 0 0 1 1 14 1 4 44 1 0 0 0 2 1 15 1 4 44 1 0 0 0 3 1 16 1 4 44 1 0 0 0 4 0 17 1 5 13 1 0 0 1 1 1 18 1 5 13 1 0 0 1 2 1 19 1 5 13 1 0 0 1 3 1 20 1 5 13 1 0 0 1 4 1
| |
The GEE solution is requested with the REPEATED statement in the GENMOD procedure. The option SUBJECT=ID(CENTER) specifies that the observations in a single cluster are uniquely identified by center and id within center . The option TYPE=UNSTR specifies the unstructured working correlation structure. The MODEL statement specifies the regression model for the mean with the binomial distribution variance function.
proc genmod data=resp descend; class id center; model outcome=center2 active female age baseline / dist=bin; repeated subject=id(center) / corr=unstr corrw; run;
These statements first produce the usual output (not shown) for fitting the generalized linear (GLM) model specified in the MODEL statement. The parameter estimates from the GLM model are used as initial values for the GEE solution. The DESCEND option in the PROC GENMOD statement specifies that the probability that outcome = 1 be modeled. If the DESCEND option had not been specified, the probability that outcome = 0 would be modeled by default.
Information about the GEE model is displayed in Output 31.5.2. The results of GEE model fitting are displayed in Output 31.5.3. If you specify no other options, the standard errors, confidence intervals, Z scores, and p -values are based on empirical standard error estimates. You can specify the MODELSE option in the REPEATED statement to create a table based on model-based standard error estimates.
| |
The GENMOD Procedure GEE Model Information Correlation Structure Unstructured Subject Effect id(center) (111 levels) Number of Clusters 111 Correlation Matrix Dimension 4 Maximum Cluster Size 4 Minimum Cluster Size 4
| |
| |
Working Correlation Matrix Col1 Col2 Col3 Col4 Row1 1.0000 0.3351 0.2140 0.2953 Row2 0.3351 1.0000 0.4429 0.3581 Row3 0.2140 0.4429 1.0000 0.3964 Row4 0.2953 0.3581 0.3964 1.0000 Analysis Of GEE Parameter Estimates Empirical Standard Error Estimates Standard 95% Confidence Parameter Estimate Error Limits Z Pr > Z Intercept 0.8882 0.4568 1.7835 0.0071 1.94 0.0519 center2 0.6558 0.3512 0.0326 1.3442 1.87 0.0619 active 1.2442 0.3455 0.5669 1.9214 3.60 0.0003 female 0.1128 0.4408 0.7512 0.9768 0.26 0.7981 age 0.0175 0.0129 0.0427 0.0077 1.36 0.1728 baseline 1.8981 0.3441 1.2237 2.5725 5.52 <.0001
| |
The non-significance of age and female make them candidates for omission from the model.
Example 31.6. Log Odds Ratios and the ALR Algorithm
Since the respiratory data in Example 31.5 are binary, you can use the ALR algorithm to model the log odds ratios instead of using working correlations to model associations. Here, a fully parameterized cluster model for the log odds ratio is fit. That is, there is a log odds ratio parameter for each unique pair of responses within clusters, and all clusters are parameterized identically. The following statements fit the same regression model for the mean as in Example 31.5 but use a regression model for the log odds ratios instead of a working correlation. The LOGOR=FULLCLUST option specifies a fully parameterized log odds ratio model.
proc genmod data=resp descend; class id center; model outcome=center2 active female age baseline / dist=bin; repeated subject=id(center) / logor=fullclust; run;
The results of fitting the model are displayed in Output 31.6.1 along with a table that shows the correspondence between the log odds ratio parameters and the within cluster pairs.
| |
The GENMOD Procedure Log Odds Ratio Parameter Information Parameter Group Alpha1 (1, 2) Alpha2 (1, 3) Alpha3 (1, 4) Alpha4 (2, 3) Alpha5 (2, 4) Alpha6 (3, 4) Analysis Of GEE Parameter Estimates Empirical Standard Error Estimates Standard 95% Confidence Parameter Estimate Error Limits Z Pr > Z Intercept 0.9266 0.4513 1.8111 0.0421 2.05 0.0400 center2 0.6287 0.3486 0.0545 1.3119 1.80 0.0713 active 1.2611 0.3406 0.5934 1.9287 3.70 0.0002 female 0.1024 0.4362 0.7526 0.9575 0.23 0.8144 age 0.0162 0.0125 0.0407 0.0084 1.29 0.1977 baseline 1.8980 0.3404 1.2308 2.5652 5.58 <.0001 Alpha1 1.6109 0.4892 0.6522 2.5696 3.29 0.0010 Alpha2 1.0771 0.4834 0.1297 2.0246 2.23 0.0259 Alpha3 1.5875 0.4735 0.6594 2.5155 3.35 0.0008 Alpha4 2.1224 0.5022 1.1381 3.1068 4.23 <.0001 Alpha5 1.8818 0.4686 0.9634 2.8001 4.02 <.0001 Alpha6 2.1046 0.4949 1.1347 3.0745 4.25 <.0001
| |
You can fit the same model by fully specifying the z -matrix. The following statements create a data set containing the full z -matrix.
data zin; keep id center z1-z6 y1 y2; array zin(6) z1-z6; set resp ; by center id; if first.id then do; t = 0; dom = 1 to 4; do n = m + 1 to 4; do j = 1 to 6; zin(j) = 0; end; y1 = m; y2 = n; t + 1; zin(t) = 1; output; end; end; end; run; proc print data=zin (obs=12);
| |
Obs z1 z2 z3 z4 z5 z6 center id y1 y2 1 1 0 0 0 0 0 1 1 1 2 2 0 1 0 0 0 0 1 1 1 3 3 0 0 1 0 0 0 1 1 1 4 4 0 0 0 1 0 0 1 1 2 3 5 0 0 0 0 1 0 1 1 2 4 6 0 0 0 0 0 1 1 1 3 4 7 1 0 0 0 0 0 1 2 1 2 8 0 1 0 0 0 0 1 2 1 3 9 0 0 1 0 0 0 1 2 1 4 10 0 0 0 1 0 0 1 2 2 3 11 0 0 0 0 1 0 1 2 2 4 12 0 0 0 0 0 1 1 2 3 4
| |
The following statements fit the model for fully parameterized clusters by fully specifying the z -matrix. The results are identical to those shown previously.
proc genmod data=resp descend; class id center; model outcome=center2 active female age baseline / dist=bin; repeated subject=id(center) / logor=zfull zdata=zin zrow =(z1-z6) ypair=(y1 y2) ; run;
Example 31.7. Log-Linear Model for Count Data
These data, from Thall and Vail (1990), are concerned with the treatment of people suffering from epileptic seizure episodes . These data are also analyzed in Diggle, Liang, and Zeger (1994). The data consist of the number of epileptic seizures in an eight-week baseline period, before any treatment, and in each of four two-week treatment periods, in which patients received either a placebo or the drug Progabide in addition to other therapy . A portion of the data is displayed in Table 31.6. See Gee Model for Count Data, Exchangeable Correlation in the SAS/STAT Sample Program Library for the complete data set.
| Patient ID | Treatment | Baseline | Visit1 | Visit2 | Visit3 | Visit4 |
|---|---|---|---|---|---|---|
| 104 | Placebo | 11 | 5 | 3 | 3 | 3 |
| 106 | Placebo | 11 | 3 | 5 | 3 | 3 |
| 107 | Placebo | 6 | 2 | 4 |
| 5 |
| . | ||||||
| . | ||||||
| . | ||||||
| 101 | Progabide | 76 | 11 | 14 | 9 | 8 |
| 102 | Progabide | 38 | 8 | 7 | 9 | 4 |
| 103 | Progabide | 19 |
| 4 | 3 |
|
| . | ||||||
| . | ||||||
| . | ||||||
Model the data as a log-linear model with V ( ¼ ) = ¼ (the Poisson variance function) and
where
-
Y ij = number of epileptic seizures in interval j
-
t ij = length of interval j
-
-

The correlations between the counts are modeled as r ij = ± , i ‰ j (exchangeable correlations). For comparison, the correlations are also modeled as independent (identity correlation matrix). In this model, the regression parameters have the interpretation in terms of the log seizure rate displayed in Table 31.7.
| Treatment | Visit | log( E ( Y ij ) /t ij ) |
|---|---|---|
| Placebo | Baseline | ² |
| 1-4 | ² + ² 1 | |
| Progabide | Baseline | ² + ² 2 |
| 1-4 | ² + ² 1 + ² 2 + ² 3 |
The difference between the log seizure rates in the pretreatment (baseline) period and the treatment periods is ² 1 for the placebo group and ² 1 + ² 3 for the Progabide group. A value of ² 3 < 0 indicates a reduction in the seizure rate.
| |
Obs id y visit trt bline age 1 104 5 1 0 11 31 2 104 3 2 0 11 31 3 104 3 3 0 11 31 4 104 3 4 0 11 31 5 106 3 1 0 11 30 6 106 5 2 0 11 30 7 106 3 3 0 11 30 8 106 3 4 0 11 30 9 107 2 1 0 6 25 10 107 4 2 0 6 25 11 107 0 3 0 6 25 12 107 5 4 0 6 25 13 114 4 1 0 8 36 14 114 4 2 0 8 36
| |
Some further data manipulations create an observation for the baseline measures, a log time interval variable for use as an offset, and an indicator variable for whether the observation is for a baseline measurement or a visit measurement. Patient 207 is deleted as an outlier, as in the Diggle, Liang, and Zeger (1994) analysis.
data new; set thall; output; if visit=1 then do; y=bline; visit=0; output; end; run; data new; set new; if id ne 207; if visit=0 then do; x1=0; ltime=log(8); end; else do; x1=1; ltime=log(2); end; run;
The GEE solution is requested by using the REPEATED statement in the GENMOD procedure. The SUBJECT=ID option indicates that the id variable describes the observations for a single cluster, and the CORRW option displays the working correlation matrix. The TYPE= option specifies the correlation structure; the value EXCH indicates the exchangeable structure.
proc genmod data=new; class id; model y=x1 trt / d=poisson offset=ltime; repeated subject=id / corrw covb type=exch; run;
These statements first produce the usual output from fitting a generalized linear model (GLM) to these data. The estimates are used as initial values for the GEE solution.
Information about the GEE model is displayed in Output 31.7.3. The results of fitting the model are displayed in Output 31.7.4. Compare these with the model of independence displayed in Output 31.7.2. The parameter estimates are nearly identical, but the standard errors for the independence case are underestimated. The coefficient of the interaction term, ² 3 , is highly significant under the independence model and marginally significant with the exchangeable correlations model.
| |
The GENMOD Procedure Analysis Of Initial Parameter Estimates Standard Wald 95% Chi Parameter DF Estimate Error Confidence Limits Square Pr > ChiSq Intercept 1 1.3476 0.0341 1.2809 1.4144 1565.44 <.0001 x1 1 0.1108 0.0469 0.0189 0.2027 5.58 0.0181 trt 1 0.1080 0.0486 0.2034 0.0127 4.93 0.0264 x1*trt 1 0.3016 0.0697 0.4383 0.1649 18.70 <.0001 Scale 0 1.0000 0.0000 1.0000 1.0000 NOTE: The scale parameter was held fixed.
| |
| |
GEE Model Information Correlation Structure Exchangeable Subject Effect id (58 levels) Number of Clusters 58 Correlation Matrix Dimension 5 Maximum Cluster Size 5 Minimum Cluster Size 5
| |
| |
Analysis Of GEE Parameter Estimates Empirical Standard Error Estimates Standard 95% Confidence Parameter Estimate Error Limits Z Pr > Z Intercept 1.3476 0.1574 1.0392 1.6560 8.56 <.0001 x1 0.1108 0.1161 0.1168 0.3383 0.95 0.3399 trt 0.1080 0.1937 0.4876 0.2716 0.56 0.5770 x1*trt 0.3016 0.1712 0.6371 0.0339 1.76 0.0781
| |
| Variable | Correlation Structure | Coef. | Std. Error | Coef./S.E. |
|---|---|---|---|---|
| Intercept | Exchangeable | 1.35 | 0.16 | 8.56 |
| Independent | 1.35 | 0.03 | 39.52 | |
| Visit ( x 1 ) | Exchangeable | 0.11 | 0.12 | 0.95 |
| Independent | 0.11 | 0.05 | 2.36 | |
| Treat ( x 2 ) | Exchangeable | ˆ’ 0.11 | 0.19 | ˆ’ 0.56 |
| Independent | ˆ’ 0.11 | 0.05 | ˆ’ 2.22 | |
| x 1 * x 2 | Exchangeable | ˆ’ 0.30 | 0.17 | ˆ’ 1.76 |
| Independent | ˆ’ 0.30 | 0.07 | ˆ’ 4.32 |
The fitted exchangeable correlation matrix is specified with the CORRW option and is displayed in Output 31.7.5.
| |
Working Correlation Matrix Col1 Col2 Col3 Col4 Col5 Row1 1.0000 0.5941 0.5941 0.5941 0.5941 Row2 0.5941 1.0000 0.5941 0.5941 0.5941 Row3 0.5941 0.5941 1.0000 0.5941 0.5941 Row4 0.5941 0.5941 0.5941 1.0000 0.5941 Row5 0.5941 0.5941 0.5941 0.5941 1.0000
| |
If you specify the COVB option, you produce both the model-based (naive) and the empirical (robust) covariance matrices. Output 31.7.6 contains these estimates.
| |
Covariance Matrix (Model-Based) Prm1 Prm2 Prm3 Prm4 Prm1 0.01223 0.001520 0.01223 0.001520 Prm2 0.001520 0.01519 0.001520 0.01519 Prm3 0.01223 0.001520 0.02495 0.005427 Prm4 0.001520 0.01519 0.005427 0.03748 Covariance Matrix (Empirical) Prm1 Prm2 Prm3 Prm4 Prm1 0.02476 0.001152 0.02476 0.001152 Prm2 0.001152 0.01348 0.001152 0.01348 Prm3 0.02476 0.001152 0.03751 0.002999 Prm4 0.001152 0.01348 0.002999 0.02931
| |
The two covariance estimates are similar, indicating an adequate correlation model.
Example 31.8. Model Assessment of Multiple Regression Using Aggregates of Residuals (Experimental)
Neter et al. (1996, Section 8.2) describe a study of 54 patients undergoing a certain kind of liver operation in a surgical unit. The data consist of the survival time and certain covariates. After a model selection procedure, they arrived at the following model
where Y is the logarithm (base 10) of the survival time, X 1 , X 2 , X 3 are blood-clotting score , prognostic index , and enzyme function , and is a normal error term. A listing of the SAS data set containing the data is shown in Output 31.8.1. The variables Y , X1 , X2 , X3 correspond to Y , X 1 , X 2 , X 3 , and LogX1 is log( X 1 ). The GENMOD fit of the model is shown in Output 31.8.2. The analysis first focuses on the adequacy of the functional form of X 1 , blood-clotting score .
| |
Obs Y X1 X2 X3 LogX1 1 2.3010 6.7 62 81 0.82607 2 2.0043 5.1 59 66 0.70757 3 2.3096 7.4 57 83 0.86923 4 2.0043 6.5 73 41 0.81291 5 2.7067 7.8 65 115 0.89209 6 1.9031 5.8 38 72 0.76343 7 1.9031 5.7 46 63 0.75587 8 2.1038 3.7 68 81 0.56820 9 2.3054 6.0 67 93 0.77815 10 2.3075 3.7 76 94 0.56820 11 2.5172 6.3 84 83 0.79934 12 1.8129 6.7 51 43 0.82607 13 2.9191 5.8 96 114 0.76343 14 2.5185 5.8 83 88 0.76343 15 2.2253 7.7 62 67 0.88649 16 2.3365 7.4 74 68 0.86923 17 1.9395 6.0 85 28 0.77815 18 1.5315 3.7 51 41 0.56820 19 2.3324 7.3 68 74 0.86332 20 2.2355 5.6 57 87 0.74819 21 2.0374 5.2 52 76 0.71600 22 2.1335 3.4 83 53 0.53148 23 1.8451 6.7 26 68 0.82607 24 2.3424 5.8 67 86 0.76343 25 2.4409 6.3 59 100 0.79934 26 2.1584 5.8 61 73 0.76343 27 2.2577 5.2 52 86 0.71600 28 2.7589 11.2 76 90 1.04922 29 1.8573 5.2 54 56 0.71600 30 2.2504 5.8 76 59 0.76343 31 1.8513 3.2 64 65 0.50515 32 1.7634 8.7 45 23 0.93952 33 2.0645 5.0 59 73 0.69897 34 2.4698 5.8 72 93 0.76343 35 2.0607 5.4 58 70 0.73239 36 2.2648 5.3 51 99 0.72428 37 2.0719 2.6 74 86 0.41497 38 2.0792 4.3 8 119 0.63347 39 2.1790 4.8 61 76 0.68124 40 2.1703 5.4 52 88 0.73239 41 1.9777 5.2 49 72 0.71600 42 1.8751 3.6 28 99 0.55630 43 2.6840 8.8 86 88 0.94448 44 2.1847 6.5 56 77 0.81291 45 2.2810 3.4 77 93 0.53148 46 2.0899 6.5 40 84 0.81291 47 2.4928 4.5 73 106 0.65321 48 2.5999 4.8 86 101 0.68124 49 2.1987 5.1 67 77 0.70757 50 2.4914 3.9 82 103 0.59106 51 2.0934 6.6 77 46 0.81954 52 2.0969 6.4 85 40 0.80618 53 2.2967 6.4 59 85 0.80618 54 2.4955 8.8 78 72 0.94448
| |
| |
The GENMOD Procedure Analysis Of Parameter Estimates Standard Wald 95% Chi- Parameter DF Estimate Error Confidence Limits Square Pr > ChiSq Intercept 1 0.4836 0.0426 0.4001 0.5672 128.71 <.0001 X1 1 0.0692 0.0041 0.0612 0.0772 288.17 <.0001 X2 1 0.0093 0.0004 0.0085 0.0100 590.45 <.0001 X3 1 0.0095 0.0003 0.0089 0.0101 966.07 <.0001 Scale 0 0.0469 0.0000 0.0469 0.0469 NOTE: The scale parameter was estimated by the square root of Pearson's Chi-Square/DOF.
| |
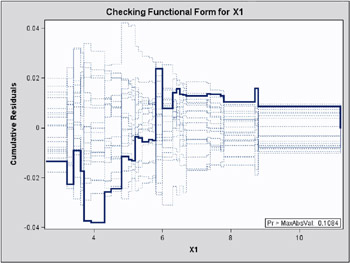
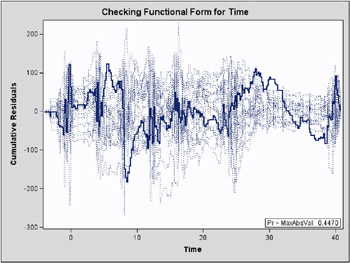
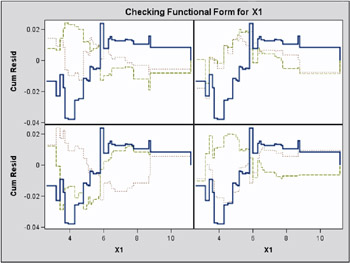
In order to assess the adequacy of the fitted multiple regression model, the ASSESS statement in the following SAS statements was used to create the plots of cumulative residuals against X1 shown in Output 31.8.3 and Output 31.8.4 and the summary table in Output 31.8.5. The RESAMPLE= keyword specifies that a p -value be computed based on a sample of 10,000 simulated residual paths. A random number seed is specified by the SEED= keyword for reproducibility . If you do not specify the seed, one is derived from the time of day. The keyword CRPANEL specifies that the panel of four cumulative residual plots shown in Output 31.8.4 be created, each with two simulated paths. The single residual plot with 20 simulated paths in Output 31.8.3 is created by default.
| |
| |
ods html; ods graphics on; proc genmod data=Surg; model Y = X1 X2 X3 / scale=Pearson; assess var=(X1) / resample=10000 seed=603708000 crpanel ; run; ods graphics off; ods html close;
These graphical displays are requested by specifying the experimental ODS GRAPHICS statement and the experimental ASSESS statement. For general information about ODS graphics, see Chapter 15, Statistical Graphics Using ODS. For specific information about the graphics available in the GENMOD procedure, see the ODS Graphics section on page 1695.
| |
Assessment Summary Maximum Assessment Absolute Pr > Variable Value Replications Seed MaxAbsVal X1 0.0380 10000 603708000 0.1084
| |
The p -value of 0.1084 reported on Output 31.8.3 and Output 31.8.5 suggests that a more adequate model may be possible. The observed cumulative residuals on Output 31.8.3 and Output 31.8.4, represented by the heavy lines, seem atypical of the simulated curves, represented by the light lines, reinforcing the conclusion that a more appropriate functional form for X1 is possible.
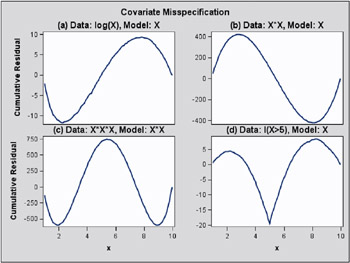
The cumulative residual plots in Output 31.8.6 provide guidance in determining a more appropriate functional form. The four curves were created from simple forms of model misspecification using simulated data. The mean models of the data and the fitted model are shown in Table 31.9.
| Plot | Data E( Y ) | Fitted Model E( Y ) |
|---|---|---|
| (a) | log( X ) | X |
| (b) | X + X 2 | X |
| (c) | X + X 2 + X 3 | X + X 2 |
| (d) | I ( X > 5) | X |
The observed cumulative residual pattern in Output 31.8.3 and Output 31.8.4 most resembles the behavior of the curve in plot (a) of Output 31.8.6, indicating that log( X 1 ) might be a more appropriate term in the model than X 1 .
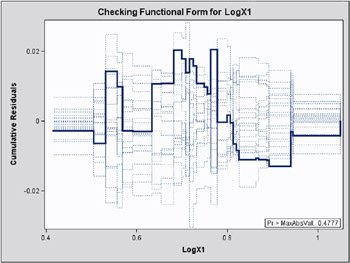
The following SAS statements fit a model with LogX1 in place of X1 and request a model assessment.
ods html; ods graphics on; proc genmod data=Surg; model Y = LogX1 X2 X3 / scale=Pearson; assess var=(LogX1) / resample=10000 seed=603708000; run; ods graphics off; ods html close;
The revised model fitisshownin Output 31.8.7, the p -value from the simulation is 0.4777, and the cumulative residuals plotted on Output 31.8.8 show no systematic trend. The log-transformation for X1 is more appropriate. Under the revised model, the p -values for testing the functional forms of X2 and X3 are 0.20 and 0.63, and the p -value for testing the linearity of the model is is 0.65. Thus, the revised model seems reasonable.
| |
The GENMOD Procedure Analysis Of Parameter Estimates Standard Wald 95% Chi- Parameter DF Estimate Error Confidence Limits Square Pr > ChiSq Intercept 1 0.1844 0.0504 0.0857 0.2832 13.41 0.0003 LogX1 1 0.9121 0.0491 0.8158 1.0083 345.05 <.0001 X2 1 0.0095 0.0004 0.0088 0.0102 728.62 <.0001 X3 1 0.0096 0.0003 0.0090 0.0101 1139.73 <.0001 Scale 0 0.0434 0.0000 0.0434 0.0434 NOTE: The scale parameter was estimated by the square root of Pearson's Chi-Square/DOF.
| |
Example 31.9. Assessment of a Marginal Model for Dependent Data Using Aggregates of Residuals (Experimental)
This example illustrates the use of cumulative residuals to assess the adequacy of a marginal model for dependent data fit by generalized estimating equations (GEEs). The assessment methods are applied to CD4 count data from an AIDS clinical trial reported by Fischl et al. (1990), and reanalyzed by Lin, Wei, and Ying (2002). The study randomly assigned 360 HIV patients to AZT and 351 to placebo. CD4 counts were measured repeatedly over the course of the study. The data used here are the 4328 measurements taken in the first 40 weeks of the study.
The analysis focuses on the time trend of the response. The first model considered is
where T ik is the time (in weeks) of the k th measurement on the i th patient, y ik is the CD4 count at T ik for the i th patient, and R i is the indicator of AZT for the i th patient. Normal errors and an independent working correlation are assumed.
The following SAS statements fit the preceding model, create the cumulative residual plot in Output 31.9.1, and compute a p -value for the model.
These graphical displays are requested by specifying the experimental ODS GRAPHICS statement and the experimental ASSESS statement. For general information about ODS graphics, see Chapter 15, Statistical Graphics Using ODS. For specific information about the graphics available in the GENMOD procedure, see the ODS Graphics section on page 1695.
Here, the SAS data set variables Time , Time2 , TrtTime , and TrtTime2 correspond to T ik , ![]() , R i T ik , and
, R i T ik , and ![]() , respectively. The variable Id identifies individual patients.
, respectively. The variable Id identifies individual patients.
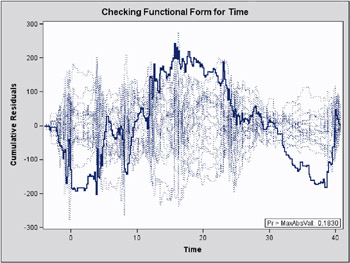
ods html; ods graphics on; proc genmod data=cd4; class Id; model Y = Time Time2 TrtTime TrtTime2; repeated sub=Id; assess var=(Time) / resample seed=603708000; run; ods graphics off; ods html close;
The cumulative residual plot in Output 31.9.1 displays cumulative residuals versus time for the model and 20 simulated realizations. The associated p -value, also shown on Output 31.9.1, is 0.18. These results indicate that a more satisfactory model might be possible. The observed cumulative residual pattern most resembles plot (c) in Output 31.8.6, suggesting cubic time trends.
The following SAS statements fit the model, create the plot in Output 31.9.2, and compute a p -value for a model with the additional terms ![]() and
and ![]() .
.
ods html; ods graphics on; proc genmod data=cd4; class Id; model Y = Time Time2 Time3 TrtTime TrtTime2 TrtTime3; repeated sub=Id; assess var=(Time) / resample seed=603708000; run; ods graphics off; ods html close;
The observed cumulative residual pattern appears more typical of the simulated realizations, and the p -value is 0.45, indicating that the model with cubic time trends is more appropriate.
EAN: N/A
Pages: 105