Chapter II: Multidimensionality in Statistical, OLAP, and Scientific Databases

Arie Shoshani, Lawrence Berkeley National Laboratory

USA

The term "multidimensional databases" refers to data that can be viewed conceptually in a multidimensional space, where each dimension represents some attributes of the data. Viewing data in this form is natural for many applications, yet the concepts are not treated in a uniform way in the database literature. In this chapter, we show the commonality of concepts between three database areas: statistical, OLAP, and scientific databases. We show that these domains have two main structural concepts: the cross-product space of the dimensions, and the classification hierarchy structure associated with each dimension. In the first part of this chapter we describe how these structures are sed to represent data in statistical and OLAP databases and how summarization operators can be applied to them. Further, we discuss how these structures can be extended to represent related information using federated database concepts. In the second part of the chapter we show that these concepts are common to many scientific database applications. In particular, we discuss the importance of supporting classification structures and the difficulty in representing them as tables in relational databases. We also discuss data structures to support multidimensional databases, emphasizing space-time representation, clustering in multidimensional space, indexing in multidimensional space, and supporting classification structures. We conclude by arguing that the concepts of multidimensionality and classification structures as well as the operation over them should be elevated to "first class" object types. These object types should be visible by the application user explicitly in the conceptual schemas as well as exposing them in the user interfaces.

INTRODUCTION AND BACKGROUND

There is a lot of data that can be viewed as multidimensional data. The term multidimensional databases typically refers to a collection of objects, each represented as a point in a multidimensional space. Even data that is represented in a tabular form, such as relations, can be thought of as multidimensional data, if each row (tuple) is thought of as an object, and the columns (attributes) are thought of as the dimensions. For example, consider the following table: employee (personID, age, sex, salary) shown in Figure 1a. If each person is represented as a point in the multidimensional space of (age, sex, salary), then that table can be represented as in Figure 1b.

Figure 1a: An "Employee" Table

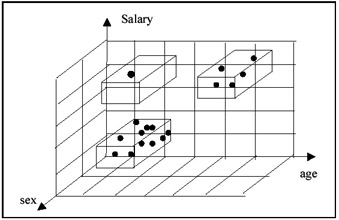
Figure 1b: A 3-D View of the Table

The utility of representing data in the multidimensional space is that it is more natural to view certain features of the data in this way. For example, it is natural to view clusters in the multidimensional space. In Figure 1b, one can easily see that there is a small cluster of highly paid people (perhaps representing managers who are generally older) and a larger cluster of lower paid people. We can also see "outliers" as is the case with the younger person with a high salary. Of course, these concepts extends to data in more than three dimensions, but cannot be viewed as easily. The problem of viewing high-dimensional data to identify clusters, outliers, and various patterns has been the subject of several research projects. An extensive review of such methods is provided in Keim & Kriegel (1996) and will not be discussed further here.

Some data is naturally multidimensional such as two-dimensional or three-dimensional spatial data. For example, climate modelers prefer to view their observed or simulated data in a multidimensional structure representing space (two or three dimensions), time, and variables being measured (temperature, wind velocity, etc.) In this case, certain operations, such a selecting spatial regions or performing the operation of "monthly means" on the data, are very common and need to be supported.

Another reason for viewing data in the multidimensional space is summarization. This need is most obvious in databases that represent statistical data or in databases used for decision support. These are referred to as "Statistical Databases" and "On-Line Analytical Processing" (OLAP), respectively. In the OLAP literature the multidimensional space is referred to as a "cube," and by selecting sub-ranges or summarizing over sub-ranges of the multidimensional space, one generates "sub-cubes."

In general, one can summarize over an entire dimension or over a region of the dimension. To illustrate a summarization over an entire dimension, consider again the database of Figure 1. One can summarize (using the operation COUNT) over the dimension "sex" to produce the lower dimensional database: "number of employees by age by salary." This is shown in Figure 2a. Note that this summarization produced a new "summary measure." Each point in this 2-D space now represents the measure: "number_of_employees." This is typical of statistical databases where the base data, called "microdata," is summarized to form "macrodata." When only part of a range is selected or summarized, the dimensionality of the product does not change. For example, selecting only lower paid younger people in the example of Figure 1 still produces a three-dimensional sub-cube.

Figure 2a: A Summary Database in 2D Space

Figure 2b: The Database Further Summarized on Each Dimension

Another aspect of statistical and OLAP databases is that each dimension can have a category hierarchy associated with it. For example, "age" can be organized as "age groups" of 1–10, 11–20, etc., and "salary" can be organized as "salary level" of "low," "medium," and "high." In this case, summarization can take place over any one of the dimensions. This action does not reduce the dimensionality of the "cube." Figure 2b shows the result of summarization of the dimensions of Figure 2a. Dimension hierarchies can get fairly complex depending on the type of dimension. For example if one of the dimensions is "products" sold in a department store, then it can have a large number of levels in the category hierarchy.

In a previous paper, we identified multidimensionality as a common aspect of both scientific and statistical databases (Shoshani & Wong, 1985). In this document, we elaborate on the concepts multidimensionality as well as category hierarchies, and discuss how they are used in summary and scientific databases in the next two sub-sections.