MULTIDIMENSIONAL DATA
|
|
Multidimensional data refer either to statistical data (Chan & Shoshani, 1981; Rafanelli & Shoshani, 1990), which mostly represent applications in the socioeconomic area, or OLAP data (Gray et al., 1996; Gyssens & Lakshmanan, 1997; Shoshani, 1997), which emphasize business applications. In the OLAP area the conceptual representation of multidimensionality by cube was proposed (see OLAP Council,. 1997; Agrawal, Gupta, & Sarawagi, 1997). According to this concept, a cube is "a group of data cells arranged by the dimensions of the data." A dimension is "a structural attribute of a cube, that is, a list of members, all of which are of a similar type in the user's perception of the data." The set of cube dimensions represents the relative data multidimensionality.
Dimensions have often been associated with different hierarchically organized levels. The levels correspond to different granularities of viewing data. The name of each cube dimension corresponds to the name of a dimension hierarchy level. We can write the following definition for a dimension:
Definition 9: A dimension D is a tuple ![]() where L is a set of levels, and ≼ is a partial order over L's elements such that
where L is a set of levels, and ≼ is a partial order over L's elements such that ![]() if dom(li) ≤ dom(lj).
if dom(li) ≤ dom(lj).
Each level belongs to one and only one dimension D; it means that for any two levels l′ ∊ D′ and l′′ ∊ D′′, l′ ∩ l′′ = Ø. Given a dimension, the shift from a lower (more detailed) level to a higher (more aggregated) level is carried out by a mapping.
This mapping is full, if:
-
each level instance of a lower level corresponds to only one level instance of a higher level;
-
each level instance of a higher level corresponds to at least one level instance of a lower level.
For the sake of simplicity, such a mapping will be called Complete containment function. It stresses that no cell contains the "Not available" value and there is no missing value.
A measure is a particular dimension of the cube as defined by Agrawal, Gupta, & Sarawagi (1997) which represents the extensional fashion of the phenomenon described by the cube, and which is in general a numeric value. The measure is obtained by a mapping from the assignment of a value to each dimension of a cube.
A cube represents factual data (for instance, sales, production, etc.) through a set of levels where each level belongs to a dimension. It can be represented simply by a triple C =< Cname, L, fc > where Cname denotes the name of the cube, L is a set of levels, and fc : LT → M is a function by which a measure (M) is associated with the tuples defined over the combinations of levels (denoted by LT).
Example 4: The above-mentioned concepts are presented through a cube shown in Figure 2. It represents a nationwide car company that owns chain stores located in all the cities. In this example, we refer to the Italian administrative territory subdivision represented in Location hierarchy.
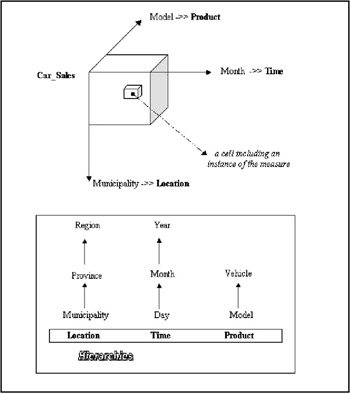
Figure 2: Example of Cube "Car_Sales"
This schema represents the multidimensional data for the sales of cars, organized at the level Month of the dimension time, the level Municipality of the dimension Location, and the level Model of the dimension Product.
The most well-known OLAP operators are roll-up, slice, and dice. The roll-up operator decreases the detail of the measure, aggregating it along the dimension hierarchy, which is summarizable. Summarizability is a condition upon which we can correctly obtain from a cube defined at level lj of a given hierarchy, another cube defined at the higher level li of the same hierarchy by using the roll-up function.
The summarizability or correctness of aggregations in OLAP is discussed in Lenz & Shoshani (1997). The authors give three necessary conditions for summarizability, and assume that these conditions are sufficient. The conditions are: disjointness of levels (or category attributes) in hierarchies; completeness in hierarchies; correct use of measure (summary attributes) with statistical functions. Disjointness implies that instances of category attributes in dimensions from disjoint subsets of the elements of a level. Completeness in hierarchies means that all the elements occur in one of the dimensions and every element is assigned to some category on the level above it in the hierarchy. Correct use of measures with statistical functions depends on the type of the measure and the statistical function.
Depending on the summarizability conditions, a default aggregate function fagg associated with the measure M must be distributive. A distributive aggregate function can be computed on a set by partitioning the set itself into disjoint subsets, aggregating each separately, and then computing the aggregation of these partial results with another aggregate function. In fact, among the SQL aggregate functions, COUNT, SUM, MIN, and MAX are distributive.
Let us consider any two levels l1 and l2 of a given hierarchy. The aggregation of measure is represented by roll-up ![]() , and it is defined by the following steps:
, and it is defined by the following steps:
-
level changing l1 → l2 will yield a new set of tuples over these more aggregated levels denoted by L′T;
-
the application of the aggregate function fc : L′T → M;
-
the resulting cube is defined by C = <Cname, L′, fc : L′T → M>.
Example 5: Let us consider the cube represented in Example 4. If we obtain the total number of cars sold in all provinces, then we have to perform roll-up![]() (Car-Sales) where fCar_Sales is a function defined as follows:
(Car-Sales) where fCar_Sales is a function defined as follows:
fCar_Sales : {model : Model, province : Province, month : Month}T → numeric; the resulting cube is defined as:
![]()
The slice operator omits one dimension of the cube and the result is a cube defined by the remaining dimensions. Let L1, L2, and L3 be the elements of L. The slice on L2 and L3 that is represented symbolically by slice ![]() consists of the next steps:
consists of the next steps:
-
it omits all the levels of L1 by projecting out L2 and L3 which yields L′ = L − L1;
-
the application of the aggregate function fc : L′T → M;
-
the resulting cube is defined by C = <Cname, L′, fc : L′T →M>.
Example 6: The number of cars sold by model and month is obtained by: ![]() , where:
, where:
fCar_Sales : {model: Model, month: Month}T → numeric, and the resulting cube is defined as:
![]()
The dice operator restricts the dimension value domain of the cube according to the built-in predicate and it is represented by diceθ (C).
Example 7: The number of cars sold in "Rome" is obtained by dicemunicipality=Rome (Car_Sales), where:

|
|
EAN: 2147483647
Pages: 150