Interpreting the Complete Laws

The detailed derivation and use of Maxwell's equations will allow you to understand the propagation of electromagnetic waves in astounding detail that will amaze your friends. However, being able to analytically determine the absolute theoretical path and power of an electromagnetic wave does not do you much good in a complex real-world environment where you know precious few of the variables needed to accurately solve the equations. The time it would take you to accurately solve the equations would ensure that your friends no longer talk to you. Intuition will serve you well in understanding the messy and complex real world. To this end, we examine the intuitive source and vortex interpretation of Maxwell's equations.

In the source and vortex interpretation, Maxwell's equations state that the electric field vector (E) can have vortices caused by changing magnetic flux; the magnetic field (H) can have vortices caused by conduction or displacement currents; the electric flux density (D) can have sources caused by conduction charge density; and the magnetic flux density vector (B) can have no sources.

In linear media, some of the statements about electric flux density (D) and magnetic flux density (B) can be extended to the electric field (E) and the magnetic field (H). However, when nonuniform fields and boundaries are considered, it can be shown that the electric field (E), the electric flux density (D), and the magnetic field (H) can have both sources and vortices, but the magnetic flux density (B) is alone in that it can have no sources.

Figures 1.1 and 1.2 provide archetypical illustrations of the source nature of the electrostatic field (Figure 1.1) and the vortex nature of a magnetic field (Figure 1.2), as well as illustrations of two of the most important boundary conditions that apply when an electric field (E) or a magnetic field (H) approaches a conducting surface.

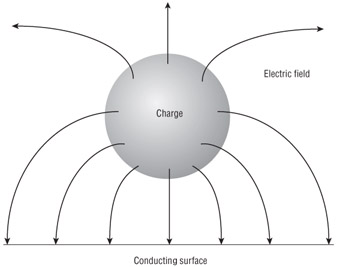
Figure 1.1: Electric field near a conducting surface

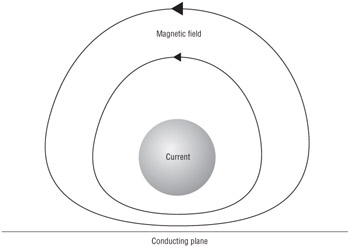
Figure 1.2: Oscillating magnetic field near a conducting plane

These boundary conditions tell us intuitively that bringing an electric charge close to a metal surface will result in most of the electric field from the charge coupling with the metal. In practice, this means that systems such as UHF RFID systems will have tag antennas couple to any and all close metal surfaces. This will result in a loss of efficiency of the antenna and usually a significant retuning of the antenna's center frequency unless the tag antenna is designed to operate near metal surfaces.

These boundary conditions also tell us that bringing a coil antenna near metal will inhibit the flow of the magnetic field around the coil. This, in turn, will decrease the coil's coupling efficiency to the reader's coiled antenna.

What we can deduce from the Complete Laws, without taking into account the properties of any materials involved, is that the tangential component of the electric field (E) is continuous across any boundary, the electric flux density (D) may be discontinuous across a boundary, and the tangential component of the magnetic field (H) may be discontinuous across a boundary.

By applying the Complete Laws to magnetic dipoles, we can identify that the distance r = λ/(2π) is of significance in determining the nature of the fields surrounding the dipoles. Within this distance, known as the near-field region, the dominant fields are the energy storage fields (that is, the magnetic fields). Beyond this distance, known as the far-field region, the dominant fields are the electromagnetic energy propagation fields that continuously transport energy away from the dipoles. Maxwell's equations correctly describe both the energy storage field and the energy propagation field.