Critical chain and activity durations

Critical chain addresses these biases in duration distributions both by addressing the behavioural causes and by turning the variability in task timing to our advantage by exploiting the statistical properties of sequences of uncertain events.

A manager applying the critical chain method will avoid student syndrome and Parkinson's Law by avoiding emphasizing a fixed delivery date when assigning tasks. Team members are rewarded if they can show that they have delivered as quickly as possible instead of being motivated to deliver on a particular day.

Using classical methods of estimating task durations, the true likely duration of each and every task gets padded with an allowance to prevent embarrassment: unless otherwise directed, most people will give an estimate of the time in which they are almost certain to be able to complete the task, whereas the average time it will take is usually shorter. This protects the estimator because they thereby reduce the chance that they will later be shown to have underestimated. Of course, for the reasons outlined above, the work normally ends up running until the deadline, even though task deadlines include this hidden padding.

Aggregating contingency

The second consequence of task estimates including contingency is that it is an extremely wasteful way to apportion contingency time. The statistics of linked processes are such that it is much better to aggregate the uncertainty into a single pool for the whole project rather than try to protect tasks one by one (see Figure A.2).

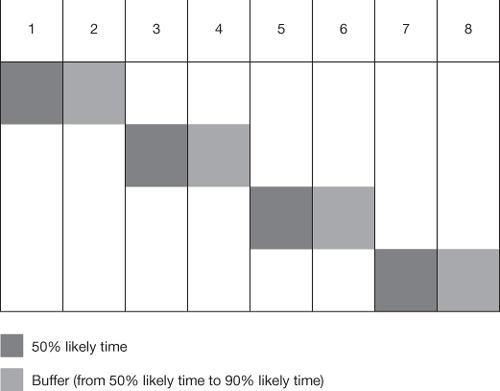
Figure A.2. The cumulative effect of buffers on each task

Consider four tasks in series, which have each been estimated to take two weeks to complete. In fact, we know that the two-week estimates are probably the time by which the tasks are 90% likely to complete, and further probing of the estimators reveals that there is a 50% probability that each task can be completed in one week. So the classical estimating method would give a chain of four two-week tasks, for a total of eight weeks.

Using critical chain, we build the plan using the one-week estimates, in the full knowledge that each of these is only 50% likely to be true, to give only four weeks in total. We allow for the uncertainty by adding a 'project buffer' which is shared between all four tasks (see Figure A.3). However, from statistics (see 'Statistics of aggregating tasks' box) we know that the uncertainty of this buffer duration is less than the sum of four individual one-week buffers. We can achieve the same overall level of protection for the project by having a two-week aggregate buffer as we did by having four one-week individual task buffers. So our critical chain plan is only six weeks long overall instead of the eight needed when each task had a buffer, and the two-week saving is due only to taking the buffers away from individual tasks and aggregating them into a single buffer for the project as a whole. Critical chain can shorten a project by over 20% in this way, with commensurate cost savings, without increasing overall risk. This may seem like black magic to project managers trained in other methods, but it is true.

Figure A.3. The effect of aggregating contingencies is to reduce the total buffer time from four weeks (Fig A.2) to two weeks

Statistics of aggregating tasks

The amount of uncertainty in a number is expressed mathematically as its standard deviation, SD or . It is also common to use variance, SD² or ², which is just the square of the standard deviation. If several uncertain processes are aggregated, then the overall variance is the sum of the variances. This is important because if the uncertainty of each number rises linearly, the uncertainty of the aggregate rises much more slowly (with the square root). For example, if four numbers each has a standard deviation of 2, then each has a variance of 2², i.e. 4. The sum of the variances is 4 x 4, i.e. 16, and the standard deviation of the aggregate of the four numbers is , i.e. 4. Treating each of the numbers separately would face us with a total uncertainty of 4 x 2, i.e. 8.

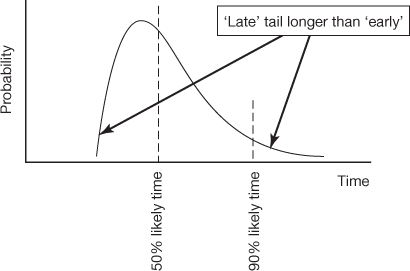
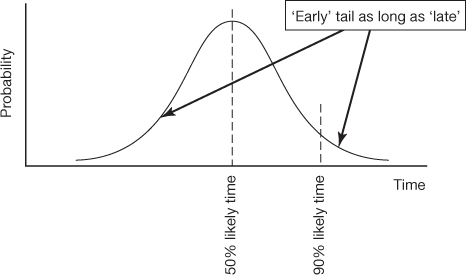
The statistics of combining many uncertain events also work to counteract the biases which make individual tasks more often late than early. The Central Limit Theorem shows that, no matter how skewed are the distributions of the durations of individual tasks, the distribution of the aggregated uncertainty will tend towards the symmetrical normal distribution as the number of tasks rises (Figure A.4). In other words, the overall project stands a reasonable chance of coming in early, even if individual tasks have a long tail on the late side (see Figure A.5)!

Figure A.4. Skewed distribution for a single task

Figure A.5. The distribution for aggregated tasks tends to the symmetrical 'normal' distribution

Top of Page