Irregular Cash Flows

All the functions discussed so far-NPV, IRR, and MIRR-deal with cash flows that are regular. That is, they occur monthly, quarterly, yearly, or at some other periodic interval. Excel provides two functions for dealing with cash flows that don't occur regularly: XNPV and XIRR.

Net Present Value

The syntax for XNPV is

 XNPV(rate,values,dates) 

The difference between XNPV and NPV is that XNPV requires a series of dates to which the values relate. In the example shown in Figure 12-18, the net present value of a series of irregular cash flows is found using XNPV.

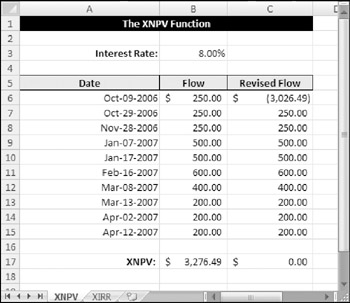
Figure 12-18: The XNPV function works with irregular cash flows.

On the CD 

The companion CD-ROM contains the workbook  irregular cash flows.xlsx, which contains all the examples in this section.

The formula in cell B17 is

 =NPV(B3,B6:B15,A6:A15) 

Similar to NPV, the result of XNPV can be checked by duplicating the cash flows and netting the result with the first cash flow. The XNPV of the revised cash flows will be zero.

Note 

Unlike the NPV function, XNPV assumes the cash flows are at the beginning of each period instead of the end. With NPV, I had to exclude the initial cash flow from the arguments and add it to the end of the formula. With XNPV, there is no need to do that.

Internal Rate of Return

The syntax for the XIRR function is

 XIRR(value,dates,guess) 

Just like XNPV, XIRR differs from its regular cousin by requiring dates. Figure 12-19 shows an example of computing the internal rate of return on a series of irregular cash flows.

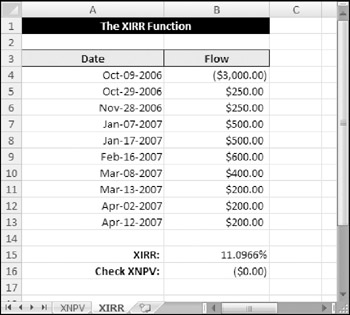
Figure 12-19: The XIRR function works with irregular cash flows.

The formula in B15 is

 =XIRR(B4:B13,A4:A13) 

Caution 

The XIRR function has the same problem with multiple rates of return as IRR. It expects that the cash flow changes signs only once: that is, goes from negative to positive or from positive to negative. If the sign changes more than once, it is essential that you plug the XIRR result back into an XNPV function to verify that it returns zero. Figure 12-19 shows such a verification although the sign only changes once in that example.