Binary Search Trees

Using the binode class from the last section, we could create a binary tree with data stored so that the value of the data in the right child as well as the value of the data in each of the descendants of the right child is greater than the value of the data of the parent. Similarly the value of the data in the left child as well as the value of the data for each of the descendants of the left child is smaller than the value of the data for the parent. For example look at the following:

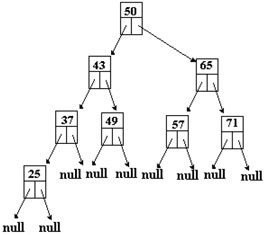
Notice how in this graphical representation of a binary tree that the descendants have a data value that is less then the parent's data value if they are on the left and greater than the parent's data value if they are on the right. A binary tree that has the data values organized like the graphical representation above is called a binary search tree or BST. This construct can be searched in a manner similar to the binary search discussed above.

As an ADT the binary search tree (BST) must have the following Basic Operations:

 •  constructor  // one or more constructors to create a BST •  destructor   // this is needed since the creation of a BST requires creating binodes    using dynamic memory allocation •  empty        // be able to determine whether the BST is empty or not •  search       // try to find an item in the BST •  insert       // place a new item in the BST •  delete       // remove an item from the BST •  traverse     // one or more methods that would move from one node to another    visiting each node at least once. 

The discussion of this section shall consider a class bst that has only the first five of these operations. The remaining will be discussed in the next section.

As with the linked lists discussed before, a bst object has as its only data member a pointer. In this case, the pointer points to an object of the binode class. This pointer will be called the root since it will be pointing to the top of the binary tree that is called the root of the tree. The definition of objects of bst will set root to point to NULL at definition time. The constructor therefore contains a statement like the following:

 root = NULL; 

As the first binode is created, root will contain the address of this binode.

The definition of the class bst must contain a member function that adds objects to the binary search tree. This function will be called: insert( ). As with the linked list before, this function will create dynamically a new binode object. These objects will be attached at the correct location by the bst object. However before a binode object can be defined or attached, the function must determine if there is a binode with the same value: item that already exists in the tree. If such a binode already exist in the tree, no binode is created and nothing is added to the binary search tree. If a binode object with the value item does not exist in the binary search tree, then a binode must be dynamically created and attached to the binary search tree at the correct point.

The first step is to determine if a binode with the value item exists. This can be done with the following code:

 binode* ptr = root, * parent = NULL; bool found = false; for(;;) {   if(found || (ptr == NULL))   break;   parent = ptr;   if(item < ptr->data)      ptr = ptr->left;   else      if(item > ptr->data)         ptr = ptr->right;      else         found = true; } 

In the above code a Boolean flag found is set to false to begin the search. It will be set to true if the value item is found in the tree. The pointer ptr is used to move down the tree. The action will go left if the value item is less than the data encountered at the binode being checked and it will go right if the value item is larger than the data at the binode. However should one of the binodes along the way have a data equal to item, then found is set to true and the loop exits. Should there be no match, then ptr will eventually point to NULL and the loop will exit in this case as well. In this case, since found was set to false to begin with, if there is no match of a data with value item during this search, then found will exit with the value of false

As the for( ) loop is exited, found will be either true or false. If it has value true, then a binode with the value item already exists and the user should be notified. If found is false, then no binode exists in the tree with data equal to item so a binode should be defined and attached. These two cases could be handled as in the following:

 if(found)    cerr << "The item " << item << " already is in the tree.\n"; else {    ptr = new binode(item);    if(parent == 0)       root = ptr;    else       if(item < (parent->data))          parent->left = ptr;       else          parent->right = ptr; } 

Notice in the else part in the code above (when found is false and therefore no binode with value item exists), the new binode is dynamically defined. The remaining code considers three cases:

1. the tree has no binodes and root will point to the new binode,

2. the new binode is placed on the left since item is less than parent->data so parent->left = ptr and

3. the new binode is placed on the right since item is greater than parent->data so parent->right = ptr

Notice that the constructor used for the binode sets both of the pointers: left and right of the new binode to NULL. If this process was followed by loading into a BST from a data file, this process could take a long time (see example in next unit).

Now that we have considered the creation of a binary search tree with binodes that were defined dynamically, we need to consider what should happen when the binary search tree goes out of scope. The memory for each dynamically defined binode must be recovered and returned to the heap. That is we must now define a destructor for the class bst that deletes each of the binodes.

The approach to these deletions is iterative and it is not very efficient because for the deletion of each node, the process begins with root. As a result, if there was a large number of binodes in the tree, this process of deletion could be a very long and involved process beginning with the root, down a branch of the tree to a leaf, delete the leaf, reset one of the parent's pointers and then delete the binode. As you can see, a large binary search tree would take some time to not only create but to destroy as well.

Notice how the following code would delete each node:

 while(!empty()) {   ptr = root;   while((ptr->left!=NULL)||(ptr->right!=NULL))   {     left_node = false;     if(ptr->left!=NULL)     {        parent = ptr;        ptr = ptr->left;        left_node = true;     }     else     {        parent = ptr;        ptr = ptr->right;     }   }   if(root==ptr)      root = NULL;   else      if(left_node)         parent->left = NULL;      else         parent->right = NULL;   delete ptr; } 

Notice that in the above code, the while( ) loop continues until the bst object is empty. That is until root == NULL.

As discussed above, the code moves down a branch of the tree until a leaf is reached. At this point, the parent for that leaf has its pointer to the leaf set to NULL and the leaf node is deleted.

The final member function to be considered in this section is search( ). This function is in fact the reason for binary search trees. That is our goal is to search the tree data for a value but in an efficient manner. The process begins like that in the insert( ) function above. The code starts at the root and works it way down the tree. There are three cases depending on the value item as compared to the data of the respective binode. The code goes left if the data of the binode is greater than the value item, it goes right if item is greater and if they are equal the Boolean found is set to true.

 for(;;) {    if(found || (ptr == NULL))      break;    if(item < ptr->data)      ptr = ptr->left;    else       if(item > ptr->data)         ptr = ptr->right;       else       {          found = true;          location = ptr;       } } return found; 

You will notice that there is a great similarity between this code and similar code in the insert( ) function. In fact the code in the insert( ) function could have included a call to the search( ) function.

The header of the function search( ) is:

 search(datatype &item,binode* &location) 

Notice the two reference operators in the signature. The one for item is only used to reduce the function's load but the reference operator for location is used to also return the address of the binode that has the value item. Using this address, the program could change the value of the data at that binode. A new search( ) function will be used in the next section. It adds an additional argument parent that will enable the deletion of individual nodes in the BST.

Putting all of these ideas together would yield the following example see bst.cpp and bst.h. This example uses Date objects from the header: date.h.