A Data Envelopment Analysis Example

[Page 140 ( continued )]

Data envelopment analysis (DEA) is a linear programming application that compares a number of service units of the same typesuch as banks, hospitals , restaurants , and schoolsbased on their inputs (resources) and outputs. The model solution result indicates whether a particular unit is less productive, or inefficient, compared to other units. For example, DEA has compared hospitals where inputs include hospital beds and staff size and outputs include patient days for different age groups.

As an example of a DEA linear programming application, consider a town with four elementary schoolsAlton, Beeks, Carey, and Delancey. The state has implemented a series of standards of learning (SOL) tests in reading, math, and history that all schools are required to administer to all students in the fifth grade. The average test scores are a measurable output of the school's performance. The school board has identified three key resources, or inputs, that affect a school's SOL scoresthe teacher-to-student ratio, supplementary funds per student (i.e., funding generated by the PTA and other private sources over and above the normal budget), and the average educational level of the parents (where 12 = high school graduate, 16 = college graduate, etc.). These inputs and outputs are summarized as follows :

input 1 = teacher-to-student ratio

input 2 = supplementary funds/student

input 3 = average educational level of parents

output 1 = average reading SOL score

output 2 = average math SOL score

output 3 = average history SOL score

[Page 141]

The actual input and output values for each school are

	Inputs			Outputs
School	1	2	3	1	2	3
Alton	.06	$260	11.3	86	75	71
Beeks	.05	320	10.5	82	72	67
Carey	.08	340	12.0	81	79	80
Delancey	.06	460	13.1	81	73	69

For example, at Alton, the teacher-to-student ratio is 0.06 (or approximately 16.67 students per teacher), there is $260 per student supplemental funds, and the average parent educational grade level is 11.3. The average scores on Alton's reading, math, and history tests are 86, 75, and 71, respectively.

Management Science Application: Analyzing Bank Branch Efficiency by Using DEA

Data envelopment analysis (DEA) is an application of linear programming that is used to determine the less productive (i.e., inefficient) service units among a group of similar service units. DEA bases this determination on the inputs (resources) and outputs of the service units.

A major northeastern bank, with 33 branches, used DEA to identify ways to improve its productivity. Bank management did not know how to identify the more efficient branches. The bank identified five resource inputs available to all branchescustomer service (tellers), sales service, management, expenses, and office space. Five groups of branch outputs were also identifieddeposits, withdrawals, and checking; bank and traveler 's checks and bonds ; night deposits; loans; and new accounts. The DEA model found that only 10 branches were operating efficiently , whereas 23 branches were using excess resources to provide their volume and mix of services and were, thus, inefficient. The DEA model results provided the basis for reviewing and evaluating branch operations, which revealed operating differences between inefficient branches and best-practice branches. The bank was able to improve its branch productivity and profits substantially, reducing its total branch staff by approximately 20% within 1 year of the completion of the DEA analysis and implementing changes in branch operations that resulted in annual savings of over $6 million.

Source: H. D. Sherman and G. Ladino, "Managing Bank Productivity Using Data Envelopment Analysis (DEA)," Interfaces 25, no. 2 (MarchApril 1995): 6073.

The school board wants to identify the school or schools that are less efficient in converting their inputs to outputs relative to the other elementary schools in the town. The DEA linear programming model will compare one particular school with all the others. For a complete analysis, a separate model is necessary for each school. For this example, we will evaluate the Delancey school as compared to the other schools.

[Page 142]

Decision Variables

The formulation of a DEA linear programming model is not as readily apparent as the previous example models in this chapter. It is particularly difficult to define the decision variables in a meaningful way.

In a DEA model, the decision variables are defined as a price per unit of each output and each input. These are not the actual prices that inputs or outputs would be valued at. In economic terms, these prices are referred to as implicit prices , or opportunity costs . These prices are a relative valuation of inputs and outputs among the schools. They do not have much meaning for us, as will become apparent as the model is developed. For now, the decision variables will simply be defined as

x _i = a price per unit of each output where i = 1, 2, 3

y _i = a price per unit of each input where i = 1, 2, 3

The Objective Function

The objective of our model is to determine whether Delancey is efficient. In a DEA model, when we are attempting to determine whether a unit (i.e., a school) is efficient, it simplifies things to scale the input prices so that the total value of a unit's inputs equals 1. The efficiency of the unit will then equal the value of the unit's outputs. For this example, this means that once we scale Delancey's input prices so that they equal 1 (which we will do by formulating a constraint), the efficiency of Delancey will equal the value of its outputs. The objective, then, is to maximize the value of Delancey's outputs, which also equals efficiency:

maximize Z = 81 x ₁ + 73 x ₂ + 69 x ₃

Because the school's inputs will be scaled to 1, the maximum value that Delancey's outputs, as formulated in the objective function, can take on is 1. If the objective function equals 1, the school is efficient; if the objective function is less than 1, the school is inefficient.

Model Constraints

The constraint that will scale the Delancey school's inputs to 1 is formulated as

.06 y ₁ + 460 y ₂ + 13.1 y ₃ = 1

This sets the value of the inputs to 1 and ultimately forces the value of the outputs to 1 or less. This also has the effect of making the values of the decision variables even less meaningful.

The values of the outputs are forced to be 1 or less by the next set of constraints. In general terms, the efficiency of a school (or any productive unit) can be defined as

It is not possible for a school or any service unit to be more than 100% efficient; thus, the efficiency of the school must be less than or equal to 1 and

[Page 143]

Converting this to standard linear form,

value of school's outputs value of schools inputs

Substituting the model's decision variables and parameters for inputs and outputs into this general constraint form results in four constraints, one for each school:

86 x ₁ + 75 x ₂ + 71 x ₃ .06 y ₁ + 260 y ₂ + 11.3 y ₃

82 x ₁ + 72 x ₂ + 67 x ₃ .05 y ₁ + 320 y ₂ + 10.5 y ₃

81 x ₁ + 79 x ₂ + 80 x ₃ .08 y ₁ + 340 y ₂ + 12.0 y ₃

81 x ₁ + 73 x ₂ + 69 x ₃ .06 y ₁ + 460 y ₂ + 13.1 y ₃

Model Summary

The complete linear programming model for determining the efficiency of the Delancey school is

The objective of this model is to determine whether Delancey is inefficient: If the value of the objective function equals 1, the school is efficient; if it is less than 1, it is inefficient. As mentioned previously, the values of the decision variables, x _i and y _i , have little meaning for us. They are the implicit prices of converting an input into an output, but they have been scaled to 1 to simplify the model. The model solution selects values of x _i and y _i that will maximize the school's efficiency, the maximum of which is 1, but these values have no easily interpretable meaning beyond that.

Computer Solution with Excel

The Excel spreadsheet for this DEA example is shown in Exhibit 4.22. The Solver window is shown in Exhibit 4.23. The decision variables are located in cells B12:B14 and D12:D14 . The objective function value, Z , which is also the indicator of whether Delancey is inefficient, is shown in cell C16. This value is computed using the formula for the value of the Delancey school's output, = B8*B12+C8*B13+D8*D14 , which is also shown in cell H8 and is a measure of the school's efficiency.

[Page 144]

Exhibit 4.22.

(This item is displayed on page 143 in the print version)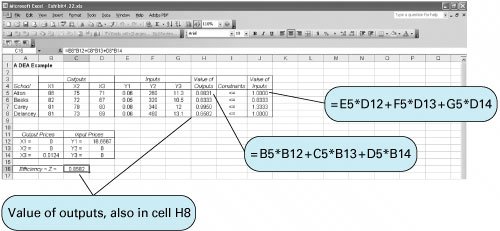

Exhibit 4.23.

The output and input values for each school are embedded in cells H5:H8 and J5:J8 , respectively. These values are used to develop the model constraints shown in Solver as H5:H8 J5:J8 . The scaling constraint is shown as J8=1 , where the formula for the value of the inputs for the Delancey school, =E8*D12+F8*D13+G8*D14 , is embedded in cell J8.

Solution Analysis

The only relevant solution value is the value of the objective function:

Z = 0.8582

Because this value is less than 1, the Delancey school is inefficient relative to the other schools. It is less efficient at converting its resources into outputs than the other schools. This means that a combination of efficient schools can achieve at least the same level of output as the Delancey school achieved with fewer input resources than required by the Delancey school. In retrospect, we can see that this is a logical result by looking back at the school's inputs and outputs. While Delancey's input values are among the highest, its output test scores are among the lowest .

It is a simple process to access the efficiency of the other three schools in the town. For example, to ascertain the efficiency of the Alton school, make the value of its output in cell H5 the objective function in Solver, and make the formula for the value of the Alton school's inputs in cell I5 the scaling constraint, I5=1 , in Solver. The efficiency of the other two schools can be assessed similarly. Doing so indicates an objective function value of 1 for each of the three other schools, indicating that all three are efficient.