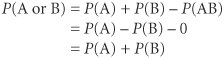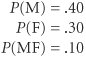Fundamentals of Probability

[Page 479 ( continued )]

Let us return to our example of a referee's tossing a coin prior to a football game. In the terminology of probability, the coin toss is referred to as an experiment . An experiment is an activity (such as tossing a coin) that results in one of the several possible outcomes. Our coin-tossing experiment can result in either one of two outcomes , which are referred to as events : a head or a tail. The probabilities associated with each event in our experiment follow:

Event	Probability
Head	.50
Tail	.50
	1.00

An experiment is an activity that results in one of several possible outcomes .

This simple example highlights two of the fundamental characteristics of probability. First, the probability of an event is always greater than or equal to zero and less than or equal to one [i.e., 0 P (event) 1.0]. In our coin-tossing example, each event has a probability of .50, which is in the range of 0 to 1.0. Second, the probability of all the events included in an experiment must sum to one . Notice in our example that the probability of each of the two events is .50, and the sum of these two probabilities is 1.0.

Two fundamentals of probability: 0 P (events) 1.0, and the probabilities of all events in an experiment sum to one .

The specific example of tossing a coin also exhibits a third characteristic: The events in a set of events are mutually exclusive . The events in an experiment are mutually exclusive if only one of them can occur at a time. In the context of our experiment, the term mutually exclusive means that any time the coin is tossed, only one of the two events can take placeeither a head or a tail can occur, but not both. Consider a customer who enters a store to shop for shoes. The store manager estimates that there is a .60 probability that the customer will buy a pair of shoes and a .40 probability that the customer will not buy a pair of shoes. These two events are mutually exclusive because it is impossible to buy shoes and not buy shoes at the same time. In general, events are mutually exclusive if only one of the events can occur, but not both.

The events in an experiment are mutually exclusive if only one can occur at a time .

Because the events in our example of obtaining a head or tail are mutually exclusive, we can infer that the probabilities of mutually exclusive events sum to 1.0 . Also, the probabilities of mutually exclusive events can be added. The following example will demonstrate these fundamental characteristics of probability.

The probabilities of mutually exclusive events sum to one .

The staff of the dean of the business school at State University has analyzed the records of the 3,000 students who received a grade in management science during the past 4 years . The dean wants to know the number of students who made each grade (A, B, C, D, or F) in the course. The dean's staff has developed the following table of information:

---

[Page 480]

Event Grade	Number of Students	Relative Frequency	Probability
A	300	300/3,000	.10
B	600	600/3,000	.20
C	1,500	1,500/3,000	.50
D	450	450/3,000	.15
F	150	150/3,000	.05
	3,000		1.00

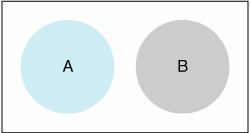
This example demonstrates several of the characteristics of probability. First, the data (numerical information) in the second column show how the students are distributed across the different grades (events). The third column shows the relative frequency with which each event occurred for the 3,000 observations. In other words, the relative frequency of a student's making a C is 1,500/3,000, which also means that the probability of selecting a student who had obtained a C at random from those students who took management science in the past 4 years is .50.

This information, organized according to the events in the experiment, is called a frequency distribution . The list of the corresponding probabilities for each event in the last column is referred to as a probability distribution .

A frequency distribution is an organization of numeric data about the events in an experiment .

All the events in this example are mutually exclusive; it is not possible for two or more of these events to occur at the same time. A student can make only one grade in the course, not two or more grades. As indicated previously, mutually exclusive probabilities of an experiment can be summed to equal one. There are five mutually exclusive events in this experiment, the probabilities of which (.10, .20, .50, .15, and .05) sum to one.

This example exhibits another characteristic of probability: Because the five events in the example are all that can occur (i.e., no other grade in the course is possible), the experiment is said to be collectively exhaustive . Likewise, the coin-tossing experiment is collectively exhaustive because the only two events that can occur are a head and a tail. In general, when a set of events includes all the events that can possibly occur, the set is said to be collectively exhaustive.

A set of events is collectively exhaustive when it includes all the events that can occur in an experiment .

The probability of a single event occurring, such as a student receiving an A in a course, is represented symbolically as P (A). This probability is called the marginal probability in the terminology of probability. For our example, the marginal probability of a student's getting an A in management science is

A marginal probability is the probability of a single event occurring .

P (A) = .10

For mutually exclusive events, it is possible to determine the probability that one or the other of several events will occur. This is done by summing the individual marginal probabilities of the events. For example, the probability of a student receiving an A or a B is determined as follows :

P (A or B) = P (A) + P (B) = .10 + .20 = .30

In other words, 300 students received an A and 600 students received a B; thus, the number of students who received an A or a B is 900. Dividing 900 students who received an A or a B by the total number of students, 3,000, yields the probability of a student's receiving an A or a B [i.e., P (A or B) = .30].

Mutually exclusive events can be shown pictorially with a Venn diagram . Figure 11.1 shows a Venn diagram for the mutually exclusive events A and B in our example.

Figure 11.1. Venn diagram for mutually exclusive events

(This item is displayed on page 481 in the print version)

A Venn diagram visually displays mutually exclusive and non-mutually exclusive events .

---

[Page 481]

Now let us consider a case in which two events are not mutually exclusive. In this case the probability that A or B or both will occur is expressed as

P (A or B) = P (A) + P (B) - P (AB)

where the term P (AB), referred to as the joint probability of A and B, is the probability that both A and B will occur. For mutually exclusive events, this term would have to equal zero because both events cannot occur together. Thus, for mutually exclusive events our formula would become

A joint probability is the probability that two or more events that are not mutually exclusive can occur simultaneously .

which is the same formula we developed previously for mutually exclusive events.

Management Science Application: Treasure Hunting with Probability and Statistics

In 1857 the SS Central America , a wooden-hulled steamship, sank during a hurricane approximately 20 miles off the coast of Charleston, South Carolina, in the Atlantic Ocean. A total of 425 passengers and crew members lost their lives, and approximately $400 million in gold bars and coins sank to the ocean bottom approximately 8,000 feet (i.e., 1.5 miles) below the surface. This shipwreck was the most famous of its time, causing a financial panic in the United States and a recommendation from insurance investigators that new ships be built with iron hulls and watertight compartments.

In 1985 the Columbus-America Discovery Group was formed to locate and recover the remains of the SS Central America . A search plan was developed, using statistical techniques and Monte Carlo simulation. From the available historical information about the wreck, three scenarios were constructed , describing different search areas based on different accounts from nearby ships and witnesses. Using historical statistical data on weather, winds and currents in the area, and estimates of uncertainties in celestial navigation, probability distributions were developed for different possible sites where the ship might have sunk. Using Monte Carlo simulation, a map was configured for each scenario, consisting of cells representing locations. Each cell was assigned a probability that the ship sank in that location. The probability maps for the three scenarios were combined into a composite probability map, which provided a guide for searching the ocean bottom using sonar. The search consisted of long, straight paths that concentrated on the high-probability areas. Based on the results of the sonar search of 1989, the discovery group recovered 1 ton of gold bars and coins from the wreck. In 1993 the total gold recovered from the wreck was valued at $21 million. However, because of the historical significance of all recovered items, they were expected to bring a much higher return when sold.

Source: L. D. Stone, "Search for the SS Central America : Mathematical Treasure Hunting," Interfaces 22, no. 1 (JanuaryFebruary 1992): 3254.

---

[Page 482]

The following example will illustrate the case in which two events are not mutually exclusive. Suppose it has been determined that 40% of all students in the school of business are at present taking management, and 30% of all the students are taking finance. Also, it has been determined that 10% take both subjects. Thus, our probabilities are

The probability of a student's taking one or the other or both of the courses is determined as follows:

P (M or F) = P (M) + P (F) P (MF) = .40 + .30 .10 = .60

Observing this formulation closely, we can see why the joint probability, P (MF), was subtracted out. The 40% of the students who were taking management also included those students taking both courses. Likewise, the 30% of the students taking finance also included those students taking both courses. Thus, if we add the two marginal probabilities, we are double-counting the percentage of students taking both courses. By subtracting out one of these probabilities (that we added in twice), we derive the correct probability.

Figure 11.2 contains a Venn diagram that shows the two events, M and F, that are not mutually exclusive, and the joint event, MF.

Figure 11.2. Venn diagram for non-mutually exclusive events and the joint event

An alternative way to construct a probability distribution is to add the probability of an event to the sum of all previously listed probabilities in a probability distribution. Such a list is referred to as a cumulative probability distribution . The cumulative probability distribution for our management science grade example is as follows:

Event Grade	Probability	Cumulative Probability
A	.10	.10
B	.20	.30
C	.50	.80
D	.15	.95
F	.05	1.00
	1.00

The value of a cumulative probability distribution is that it organizes the event probabilities in a way that makes it easier to answer certain questions about the probabilities. For example, if we want to know the probability that a student will get a grade of C or higher , we can add the probabilities of the mutually exclusive events A, B, and C:

P (A or B or C) = P (A) + P (B) + P (C) = .10 + .20 + .50 = .80

Or we can look directly at the cumulative probability distribution and see that the probability of a C and the events preceding it in the distribution (A and B) equals .80. Alternatively, if we want to know the probability of a grade lower than C, we can subtract the cumulative probability of a C from 1.00 (i.e., 1.00 .80 = .20).