[Page 404]4.5. Design Issues for Paging Systems In the previous sections we have explained how paging works and have given a few of the basic page replacement algorithms and shown how to model them. But knowing the bare mechanics is not enough. To design a system, you have to know a lot more to make it work well. It is like the difference between knowing how to move the rook, knight, and other pieces in chess, and being a good player. In the following sections, we will look at other issues that operating system designers must consider in order to get good performance from a paging system. 4.5.1. The Working Set Model In the purest form of paging, processes are started up with none of their pages in memory. As soon as the CPU tries to fetch the first instruction, it gets a page fault, causing the operating system to bring in the page containing the first instruction. Other page faults for global variables and the stack usually follow quickly. After a while, the process has most of the pages it needs and settles down to run with relatively few page faults. This strategy is called demand paging because pages are loaded only on demand, not in advance. Of course, it is easy enough to write a test program that systematically reads all the pages in a large address space, causing so many page faults that there is not enough memory to hold them all. Fortunately, most processes do not work this way. They exhibit a locality of reference, meaning that during any phase of execution, the process references only a relatively small fraction of its pages. Each pass of a multipass compiler, for example, references only a fraction of the pages, and a different fraction at that. The concept of locality of reference is widely applicable in computer science, for a history see Denning (2005). The set of pages that a process is currently using is called its working set (Denning, 1968a; Denning, 1980). If the entire working set is in memory, the process will run without causing many faults until it moves into another execution phase (e.g., the next pass of the compiler). If the available memory is too small to hold the entire working set, the process will cause numerous page faults and run slowly since executing an instruction takes a few nanoseconds and reading in a page from the disk typically takes 10 milliseconds. At a rate of one or two instructions per 10 milliseconds, it will take ages to finish. A program causing page faults every few instructions is said to be thrashing (Denning, 1968b). In a multiprogramming system, processes are frequently moved to disk (i.e., all their pages are removed from memory) to let other processes have a turn at the CPU. The question arises of what to do when a process is brought back in again. Technically, nothing need be done. The process will just cause page faults until its working set has been loaded. The problem is that having 20, 100, or even 1000 page faults every time a process is loaded is slow, and it also wastes considerable CPU time, since it takes the operating system a few milliseconds of CPU time to process a page fault, not to mention a fair amount of disk I/O.
[Page 405]Therefore, many paging systems try to keep track of each process' working set and make sure that it is in memory before letting the process run. This approach is called the working set model (Denning, 1970). It is designed to greatly reduce the page fault rate. Loading the pages before letting processes run is also called prepaging. Note that the working set changes over time. It has long been known that most programs do not reference their address space uniformly Instead the references tend to cluster on a small number of pages. A memory reference may fetch an instruction, it may fetch data, or it may store data. At any instant of time, t, there exists a set consisting of all the pages used by the k most recent memory references. This set, w(k, t), is the working set. Because a larger value of k means looking further into the past, the number of pages counted as part of the working set cannot decrease as k is made larger. So w(k, t) is a monotonically nondecreasing function of k. The limit of w(k, t) as k becomes large is finite because a program cannot reference more pages than its address space contains, and few programs will use every single page. Figure 4-18 depicts the size of the working set as a function of k. Figure 4-18. The working set is the set of pages used by the k most recent memory references. The function w(k, t) is the size of the working set at time t. 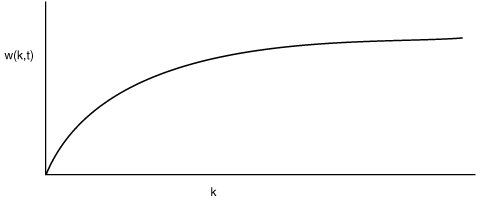
The fact that most programs randomly access a small number of pages, but that this set changes slowly in time explains the initial rapid rise of the curve and then the slow rise for large k. For example, a program that is executing a loop occupying two pages using data on four pages, may reference all six pages every 1000 instructions, but the most recent reference to some other page may be a million instructions earlier, during the initialization phase. Due to this asymptotic behavior, the contents of the working set is not sensitive to the value of k chosen. To put it differently, there exists a wide range of k values for which the working set is unchanged. Because the working set varies slowly with time, it is possible to make a reasonable guess as to which pages will be needed when the program is restarted on the basis of its working set when it was last stopped. Prepaging consists of loading these pages before the process is allowed to run again.
[Page 406]To implement the working set model, it is necessary for the operating system to keep track of which pages are in the working set. One way to monitor this information is to use the aging algorithm discussed above. Any page containing a 1 bit among the high order n bits of the counter is considered to be a member of the working set. If a page has not been referenced in n consecutive clock ticks, it is dropped from the working set. The parameter n has to be determined experimentally for each system, but the system performance is usually not especially sensitive to the exact value. Information about the working set can be used to improve the performance of the clock algorithm. Normally, when the hand points to a page whose R bit is 0, the page is evicted. The improvement is to check to see if that page is part of the working set of the current process. If it is, the page is spared. This algorithm is called wsclock. 4.5.2. Local versus Global Allocation Policies In the preceding sections we have discussed several algorithms for choosing a page to replace when a fault occurs. A major issue associated with this choice (which we have carefully swept under the rug until now) is how memory should be allocated among the competing runnable processes. Take a look at Fig. 4-19(a). In this figure, three processes, A, B, and C, make up the set of runnable processes. Suppose A gets a page fault. Should the page replacement algorithm try to find the least recently used page considering only the six pages currently allocated to A, or should it consider all the pages in memory? If it looks only at A's pages, the page with the lowest age value is A5, so we get the situation of Fig. 4-19(b). Figure 4-19. Local versus global page replacement. (a) Original configuration. (b) Local page replacement. (c) Global page replacement. (This item is displayed on page 407 in the print version) 
On the other hand, if the page with the lowest age value is removed without regard to whose page it is, page B3 will be chosen and we will get the situation of Fig. 4-19(c). The algorithm of Fig. 4-19(b) is said to be a local page replacement algorithm, whereas that of Fig. 4-19(c) is said to be a global algorithm. Local algorithms effectively correspond to allocating every process a fixed fraction of the memory. Global algorithms dynamically allocate page frames among the runnable processes. Thus the number of page frames assigned to each process varies in time. In general, global algorithms work better, especially when the working set size can vary over the lifetime of a process. If a local algorithm is used and the working set grows, thrashing will result, even if there are plenty of free page frames. If the working set shrinks, local algorithms waste memory. If a global algorithm is used, the system must continually decide how many page frames to assign to each process. One way is to monitor the working set size as indicated by the aging bits, but this approach does not necessarily prevent thrashing. The working set may change size in microseconds, whereas the aging bits are a crude measure spread over a number of clock ticks.
[Page 407]Another approach is to have an algorithm for allocating page frames to processes. One way is to periodically determine the number of running processes and allocate each process an equal share. Thus with 12,416 available (i.e., nonoperating system) page frames and 10 processes, each process gets 1241 frames. The remaining 6 go into a pool to be used when page faults occur. Although this method seems fair, it makes little sense to give equal shares of the memory to a 10-KB process and a 300-KB process. Instead, pages can be allocated in proportion to each process' total size, with a 300-KB process getting 30 times the allotment of a 10-KB process. It is probably wise to give each process some minimum number, so it can run, no matter how small it is. On some machines, for example, a single two-operand instruction may need as many as six pages because the instruction itself, the source operand, and the destination operand may all straddle page boundaries. With an allocation of only five pages, programs containing such instructions cannot execute at all. If a global algorithm is used, it may be possible to start each process up with some number of pages proportional to the process' size, but the allocation has to be updated dynamically as the processes run. One way to manage the allocation is to use the PFF (Page Fault Frequency) algorithm. It tells when to increase or decrease a process' page allocation but says nothing about which page to replace on a fault. It just controls the size of the allocation set. For a large class of page replacement algorithms, including LRU, it is known that the fault rate decreases as more pages are assigned, as we discussed above. This is the assumption behind PFF. This property is illustrated in Fig. 4-20.
[Page 408] Figure 4-20. Page fault rate as a function of the number of page frames assigned. 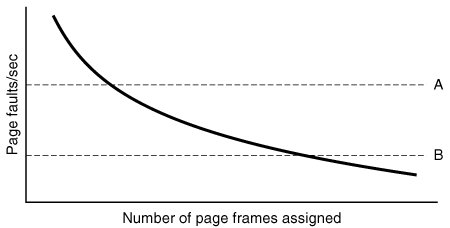
Measuring the page fault rate is straightforward: just count the number of faults per second, possibly taking a running mean over past seconds as well. One easy way to do this is to add the present second's value to the current running mean and divide by two. The dashed line marked A corresponds to a page fault rate that is unacceptably high, so the faulting process is given more page frames to reduce the fault rate. The dashed line marked B corresponds to a page fault rate so low that it can be concluded that the process has too much memory. In this case, page frames may be taken away from it. Thus, PFF tries to keep the paging rate for each process within acceptable bounds. If it discovers that there are so many processes in memory that it is not possible to keep all of them below A, then some process is removed from memory, and its page frames are divided up among the remaining processes or put into a pool of available pages that can be used on subsequent page faults. The decision to remove a process from memory is a form of load control. It shows that even with paging, swapping is still needed, only now swapping is used to reduce potential demand for memory, rather than to reclaim blocks of it for immediate use. Swapping processes out to relieve the load on memory is reminiscent of two-level scheduling, in which some processes are put on disk and a short-term scheduler is used to schedule the remaining processes. Clearly, the two ideas can be combined, with just enough processes swapped out to make the page-fault rate acceptable. 4.5.3. Page Size The page size is often a parameter that can be chosen by the operating system. Even if the hardware has been designed with, for example, 512-byte pages, the operating system can easily regard pages 0 and 1, 2 and 3, 4 and 5, and so on, as 1-KB pages by always allocating two consecutive 512-byte page frames for them. Determining the best page size requires balancing several competing factors. As a result, there is no overall optimum. To start with, there are two factors that argue for a small page size. A randomly chosen text, data, or stack segment will not fill an integral number of pages. On the average, half of the final page will be empty. The extra space in that page is wasted. This wastage is called internal fragmentation. With n segments in memory and a page size of p bytes, np/ 2 bytes will be wasted on internal fragmentation. This argues for a small page size.
[Page 409] Another argument for a small page size becomes apparent if we think about a program consisting of eight sequential phases of 4 KB each. With a 32-KB page size, the program must be allocated 32 KB all the time. With a 16-KB page size, it needs only 16 KB. With a page size of 4 KB or smaller, it requires only 4 KB at any instant. In general, a large page size will cause more unused program to be in memory than a small page size. On the other hand, small pages mean that programs will need many pages, hence a large page table. A 32-KB program needs only four 8-KB pages, but 64 512-byte pages. Transfers to and from the disk are generally a page at a time, with most of the time being for the seek and rotational delay, so that transferring a small page takes almost as much time as transferring a large page. It might take 64 x 10 msec to load 64 512-byte pages, but only 4 x 10.1 msec to load four 8-KB pages. On some machines, the page table must be loaded into hardware registers every time the CPU switches from one process to another. On these machines having a small page size means that the time required to load the page registers gets longer as the page size gets smaller. Furthermore, the space occupied by the page table increases as the page size decreases. This last point can be analyzed mathematically. Let the average process size be s bytes and the page size be p bytes. Furthermore, assume that each page entry requires e bytes. The approximate number of pages needed per process is then s/p, occupying se/p bytes of page table space. The wasted memory in the last page of the process due to internal fragmentation is p/ 2. Thus, the total overhead due to the page table and the internal fragmentation loss is given by the sum of these two terms: overhead = se/p + p/2 The first term (page table size) is large when the page size is small. The second term (internal fragmentation) is large when the page size is large. The optimum must lie somewhere in between. By taking the first derivative with respect to p and equating it to zero, we get the equation 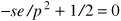
From this equation we can derive a formula that gives the optimum page size (considering only memory wasted in fragmentation and page table size). The result is: 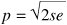
[Page 410]For s = 1MB and e = 8 bytes per page table entry, the optimum page size is 4 KB. Commercially available computers have used page sizes ranging from 512 bytes to 1 MB. A typical value used to 1 KB, but nowadays 4 KB or 8 KB are more common. As memories get larger, the page size tends to get larger as well (but not linearly). Quadrupling the RAM size rarely even doubles the page size. 4.5.4. Virtual Memory Interface Up until now, our whole discussion has assumed that virtual memory is transparent to processes and programmers. That is, all they see is a large virtual address space on a computer with a small(er) physical memory. With many systems, that is true, but in some advanced systems, programmers have some control over the memory map and can use it in nontraditional ways to enhance program behavior. In this section, we will briefly look at a few of these. One reason for giving programmers control over their memory map is to allow two or more processes to share the same memory. If programmers can name regions of their memory, it may be possible for one process to give another process the name of a memory region so that process can also map it in. With two (or more) processes sharing the same pages, high bandwidth sharing becomes possible: one process writes into the shared memory and another one reads from it. Sharing of pages can also be used to implement a high-performance message passing system. Normally, when messages are passed, the data are copied from one address space to another, at considerable cost. If processes can control their page map, a message can be passed by having the sending process unmap the page(s) containing the message, and the receiving process mapping them in. Here only the page names have to be copied, instead of all the data. Yet another advanced memory management technique is distributed shared memory (Feeley et al., 1995; Li and Hudak, 1989; and Zekauskas et al., 1994). The idea here is to allow multiple processes over a network to share a set of pages, possibly, but not necessarily, as a single shared linear address space. When a process references a page that is not currently mapped in, it gets a page fault. The page fault handler, which may be in the kernel or in user space, then locates the machine holding the page and sends it a message asking it to unmap the page and send it over the network. When the page arrives, it is mapped in and the faulting instruction is restarted. |


