8.3 Calibrating the lattice to an observed term structure
8.3 Calibrating the lattice to an observed term structure
The market convention for quoting a term structure is in terms of annualised yields of zero coupon bonds of various maturities. Therefore if y is the N year rate, then the current price of the associated zero coupon bond [2] is:
Calibration of the tree involves finding the one-period yield (short-term interest rate) at each node, such that the observed term structure is matched. The following methodology for calibrating the binomial tree to a market-observed interest rate and volatility term structure is outlined by BDT [ 6 ].
Consider the interest rate and volatility term structures observed at time
t = 0, represented by {( y i , ƒ i ): i =1, , N } where y i is the yield of a zero coupon bond with maturity t = i and ƒ i the corresponding volatility. For simplicity, assume that each time interval in the tree is one year and we wish to calibrate the tree such that the yield and volatility term structures are matched. For shorter time steps we would require the observed yields and volatilities at more frequent time intervals.
At time t = 0, the short-term interest rate may be taken directly from the observed term structure as the 1-year yield, hence r = y 1 . To determine the short-term interest rates at time t = 1, make use of the observed 2-year yield and associated volatility. The current value of a 2-year zero coupon bond, P (2) = P (2) is calculated as:
At time t = 1, the 2-year zero coupon bond has one year left to run, so its prices, P (2) u and P (2) d (where the subscript indicates an up or down move in the short-term interest rate), may be found as:
where r u and r d are the time t = 1 short-term interest rates resulting from an up move and down move respectively. These time t = 1 bond prices must be such that discounting by the t = 0 short-term interest rate r , we obtain the time t = 0 price of the 2-year zero coupon bond, P (2) . That is:
We also need to match the term structure of volatilities. The standard deviation of the short-term interest rate at time t = 1 is matched to the volatility of the 2-year yield ƒ 2 , hence [3] :
The equations (8.3)-(8.5) are solved simultaneously for the four unknowns:
The resulting t = 1 short-term interest rates r u and r d are exactly consistent with the 2-year term structure of yields and volatilities. To determine the possible short-term interest rates at t = 2, make use of the 3-year yield and volatility. There are three possible short-term interest rates at t =2, r uu , r du = r ud and r dd , but only two known values, the yield and volatility, to which we calibrate. This means that the solution is not unique. However, the short-term interest rate volatility is a function of time only, therefore:
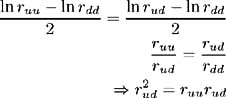
and hence, we need only match two short-term interest rates to two observed values and can find a unique solution.

Figure 8.3: Tree of short-term interest rates out to 2 years
[2] Assume all zero coupon bonds have a maturity value of 100.
[3] Consider a random variable X . At time t = t *, X may take on two possible values, x 1 and x 2 , each with probability ½. Without loss of generality, let x 1 ‰ x 2 . Hence:
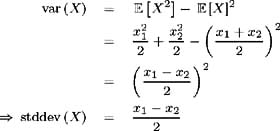
EAN: 2147483647
Pages: 132