Appendix H: Monte Carlo Simulation

OVERVIEW

Decisions approaches include pure intuition and judgment, experience and analogy with similar situations, analysis with the aid of analytical models, experimentation with real systems, and experimentation with a model of a real system.

Simulation is associated with the last approach. It uses a model of a system and manipulates it so as to imitate the system's behavior over time for the purpose of evaluating alternative design characteristics or decision rules. It is a systematic trial-and-error method for solving complex problems. Simulation makes available an experimental laboratory for the experimenter by making it possible to test various alternatives without risking or committing organizational resources. The effects of numerous alternative policies can be ascertained without tampering with the actual system. This form of system experimentation can reduce the risk of upsetting the existing structure with changes that would not be beneficial. Simulation gives the manager an opportunity to test and evaluate proposals without running the risk of actually installing new approaches and absorbing the costs associated with the changes. With simulation, "trial and error" need not become "trial and catastrophe."

When problems involve risk or uncertainty, an analytical solution may be difficult or impossible to obtain. Simulation is useful in situations where analytical solutions are not appropriate because the models are either too complex or too costly. A mathematical model using the analytical approach can become incredibly complex because of numerous interacting variables . Simulation offers an alternative for complex problems not suitable for rigorous analytical analysis.

Simulation develops a model of some phenomenon and then performs experiments on the model. It is a descriptive rather than an optimization technique, which means that it does not yield optimal solutions. Monte Carlo simulation is a numerical technique that models a probabilistic system with the intention of predicting the system's behavior.

Monte Carlo simulation involves determining the probability distributions of the variables under study and then sampling from the distributions by using random numbers to obtain data. It is a probabilistic type of simulation that approximates the solution to a problem by sampling from a random process. A series of random numbers is used to describe the movement of each random variable over time. The random numbers allow an artificial but realistic sequence of events to occur. Monte Carlo simulation permits the experimenter to determine how varied policies or organizational conditions will be modified by the behavior of random or transient influences. A general approach to solving problems by Monte Carlo simulation is contained in Figure H.1.

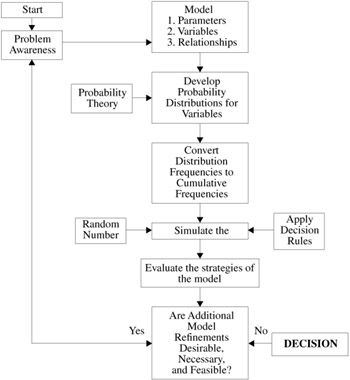
Figure H.1: Monte Carlo simulation.

Monte Carlo simulation establishes a stochastic model of a real situation and then performs sampling experiments on the model. This technique generates a vast amount of data that might otherwise take a very long time to obtain. Following the generation of data, computations can be made and a problem solution derived.

The major steps in Monte Carlo simulation are as follows :

1. Make sure that you know the probability distributions of certain key variables of the problem must be known distributions. They may be standard distributions such as the Poisson, normal, or exponential, or they may be empirical distributions obtained from historical records.

2. Convert the frequency distributions to cumulative probability distributions. This assures that only one variable value will be associated with a given random number.

3. Sample at random from the cumulative probability distributions to determine specific variable values to use in the simulation. A way to sample is to use numbers from a table of random numbers. The random numbers are inserted in the cumulative probability distributions to obtain specific variable values for each observation. The sequence of assigned random numbers will imitate the pattern of variation expected to be encountered .

4. Simulate the operation under analysis for a large number of observations. The appropriate number of replications is determined in the same manner as the appropriate size of a sample in an actual experiment in the real world. The ordinary statistical tests of significance can be used. With computerized simulation the size of the sample can be increased without difficulty, and it is economical to run large samples with very small sampling errors.

Everything depends on the choice of frequency distributions. Unless there is some assurance they have been picked well, the entire simulation can be worthless. Distributions can be obtained from historical records or experimentation or chosen a priori on a quasi- subjective basis.

Random numbers are the life blood of the method and are numbers of equal long run frequency. They completely lack sequential predictability. The randomness of tabulated numbers can be validated by a chi-square test. The stream of random numbers can be obtained from a published table, or a computer can generate effectively random numbers (called pseudo-random numbers) internally.

Monte Carlo simulation has many practical uses, such as waiting line problems (where standard distributions for arrival rates and service rates are inadequate), layout problems of multiphase assembly lines, inventory problems, equipment replacement problems, engineering tolerancing and so on.

A simulation model does not produce an optimum solution. The experimenter selects the alternatives to evaluate by simulation but cannot be sure that the best alternative has been included. The simulation indicates possible solutions based only on the input of alternatives selected by the manager; it does not indicate which alternatives to evaluate. Simulation models usually develop heuristic rather than analytical solutions to a problem, but they can deal with very complex situations that defy solution by analytical methods .

No analytical solution can be extricated from its premises and assumptions. Simulation can investigate the effect of a relaxation of assumptions. Also, when no analytical solution is possible, simulation becomes important as a last resort. While simulation does not promise optimal solutions, it does allow picking out the best one tried. The ability of simulation to handle dependent variable interactions renders it a very powerful tool of systems analysis.

Simulation is used to reproduce a typical series of events (usually in mathematical form) that could have occurred in practice. If enough events are simulated and mean values determined, it can be assumed that they represent what would probably have happened in practice if the real situation existed. Standard statistical tests can be run on the output to determine when stability occurs.

Initial transient phenomena such as oscillations, rapid growth, and sudden decay are not unusual in simulation (or in reality). If system stability is desired, a sufficient startup period should be allowed for stability to develop. In real life, such transient phenomena are commonplace occurrences. Whereas analytical methods are usually based on steady-state conditions, simulation need not be limited by these assumptions.