Polar Coordinates Versus Cartesian Coordinates
| < Day Day Up > |
| In the preceding section, you found that positive or negative is sufficient for the direction of a vector in one dimension. However, in 2D and 3D, positive or negative just isn't enough. There are two different forms for describing a vector in 2D: polar coordinates and Cartesian coordinates. Polar coordinates are a little more intuitive, so let's look at them first.
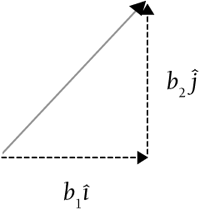
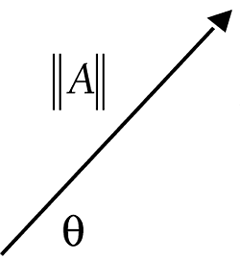
Figure 4.2 illustrates polar coordinates. Figure 4.2. Vector A expressed in polar coordinates. NOTE Notice that vector A is a capital letter. This text uses capital letter notation for vectors. Some sources use the arrow notation, which is written Polar coordinates are the easiest way to visualize what a vector looks like. This is why we spent time establishing a standard position for angles in Chapter 3, "Trigonometry Snippets." Now when we express a vector as a magnitude with a direction, the direction is simply an angle in standard position. This takes care of all the possible directions in 2D. Cartesian coordinates are less intuitive, but that is the form used for coding vectors. Rather than describe a vector by its length and direction, you can also describe it by its horizontal and vertical displacement, much like with the Cartesian coordinate system. These two pieces are called the horizontal and vertical components , and they're written in what I call "i and j form."
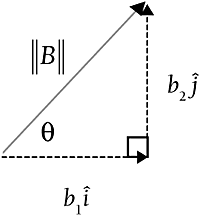
Figure 4.3 illustrates Cartesian coordinates. Figure 4.3. Vector B expressed in Cartesian coordinates. NOTE The i and j form might look strange because of the "caps" over the i and j. Just read Also note that the components might be negative, which just indicates left or down rather than right or up. The computer screen is set up in a gridlike fashion, which is why coding is done in Cartesian coordinates. Quite often you plan with vector quantities in polar form but then need to code them in Cartesian form. Therefore, let's look at the process of converting from polar coordinates to Cartesian. If you look at vector A shown in Figure 4.4, you'll see that you can create a right triangle and use the trig functions to convert from polar to Cartesian coordinates. Figure 4.4. Converting from polar to Cartesian coordinates.
Example 4.4: Converting from Polar to Cartesian CoordinatesVector A is a displacement vector. Convert A = 20m @ 30 to Cartesian coordinates. SolutionYou can use sine and cosine to break A into components: Therefore,
Figure 4.5 illustrates this process. Figure 4.5. Converting from Cartesian to polar coordinates. Example 4.5: Converting from Cartesian to Polar Coordinates Convert vector Solution
Therefore, B = 5 units @ 53.1 in polar coordinates. Let's take a look at some functions which could solve the preceding problems for us. First, we need to define our data types that we're going to be using: // A structure for holding a vector in component form struct 2Dvector_comp { float x, y; }; // A structure for holding a vector in magnitude/direction form struct 2Dvector_polar { float mag, dir; }; Now let's write two functions which convert from component to magnitude/direction form and vice versa: // purpose: to convert a vector from magnitude/direction to component form // input: vec- a vector in magnitude/direction form // output: our converted vector 2Dvector_comp_PolarToCompConversion(2Dvector_polar vec) { // A temporary variable which will hold our answer 2Dvector_comp temp; // Fill in our values temp.x = mag * cos(dir * PI / 180); temp.y = mag * sin(dir * PI / 180); // Return our answer return temp; } // purpose: to convert a vector from component to magnitude/direction form // input: vec- a vector in component form // output: our converted vector 2Dvector_polar_CompToPolarConversion(2Dvector_comp vec) { // A temporary variable which will hold our answer 2Dvector_polar temp = { 0, 0 }; // Calculate our magnitude using the Pythagorean theorom temp.mag = sqrtf(vec.x * vec.x + vec.y * vec.y); // Error check to prevent a divide-by-zero issue in our next section if(temp.mag == 0) return temp; // Caculate our angle. We are using asin() which will return an angle // in either the 1 st or the 4 th quadrant temp.dir = (180 / PI) * asin(vec.y / temp.mag); // Adjust our angle in the event that it lies in the 2 nd or 3 rd quadrant if(vec.x < 0) temp.dir += 180; // Adjust our angle in the event that it lies in the 4 th quadrant else if(vec.x > 0 && vec.y < 0) temp.dir += 360; // Return our new vector return temp; } Another benefit of Cartesian form (besides the fact that the computer requires it) is that it can very easily be extended to 3D.
If you haven't already noticed, as mathematical concepts get implemented in the world of programming, often the notations change. A vector in Cartesian form is often written as a single-row or single-column matrix rather than in the traditional i and j form. For example, the 2D matrix Similarly, a 3D vector The discussion of normalizing vectors in the "Scalar Multiplication" section later in this chapter, uses a single-row matrix to represent a vector in Cartesian coordinates, so don't be intimidated. Self-Assessment
|
| < Day Day Up > |
EAN: 2147483647
Pages: 143
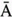 . They both mean the same thing. Also note that the @ symbol is pronounced "at." For example, 20m @ 30 is read as "20 meters at 30 degrees in standard position."
. They both mean the same thing. Also note that the @ symbol is pronounced "at." For example, 20m @ 30 is read as "20 meters at 30 degrees in standard position."