4.5 A Biomolecular Reaction-Diffusion Processor: Basic Principles
|
4.5 A Biomolecular Reaction-Diffusion Processor: Basic Principles
The conception of a medium that is able to carry out continuous chemical information processing forms the basis of implementing the reaction-diffusion paradigm.
The principal scheme of a biomolecular computer (see Rambidi, Chernavskii, and Krinsky 1993) is shown in figure 4.2.
-
Input of information. The macro-micro interface unit transforms an information input (some distribution of external physical stimuli) into a corresponding distribution of molecular components. The most widely known example is a medium containing photosensitive molecules subject to photochemical reactions under a predetermined spatial distribution of light radiation. As a result, the intensity of light radiation is converted into a distribution of reaction product concentrations. The resources of such interface units would be significantly increased by using a set of molecules sensitive to the radiation in different frequency ranges, by using a combination of different physical stimuli, and so on.
-
Information processing. The information processing capabilities of a medium should be determined by the composition of molecular components in the processor medium.
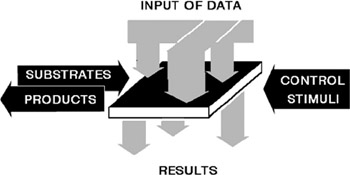
Figure 4.2: Schematic representation of a biomolecular reaction-diffusion processor.
The main methodology for choosing the medium is determined by the following rules:
-
Molecular forms released as a result of information input should represent the initial information for a chemical processing system—that is, for a set of coupled chemical reactions.
-
The general scheme of the reaction set (and also their substrates and products) should be chosen in a way that is adequate for the information processing task at hand.
-
Output of results. The micro-macro interface for the information processing medium should be a system capable of measuring the distribution of molecular component concentrations corresponding to the final result of the computation. The most convenient versions of such units seem to be different spectrometric systems capable of measuring the spatial distribution of molecular concentrations with appropriate spatial and temporal resolution.
-
Control and power supply. The power supply of the biomolecular processor should be of a chemical nature. It is necessary to input continuously (in general) the substrates of the chemical reactions used and to remove the products of these reactions. The control of the processor and data input can be carried out by physical or chemical stimuli affecting the system. Suggested methods are:
-
Electromagnetic, mostly visible light radiation
-
Local electrical fields
-
Local input of controlling molecules or ions
-
And so on
The fundamental and most important feature of the reaction-diffusion processor conception is that a reaction-diffusion biomolecular computer is an instance machine (Zauner and Conrad 1996; Rambidi 1997)—that is, the opposite extreme of a universal computer—and it represents an information processing device that encodes a single problem instance in its structure.
There are two basic properties typical for an instance machine:
-
The physical structure of the machine is specific for a single problem instance.
-
The temporal evolution of the machine leads, under conditions predetermined by the problem under solution, to a state or structure that can be interpreted as a solution of this problem.
A biomolecular processor based on nonlinear dynamic mechanisms is the instance machine. Given a single problem, its solution is determined by an appropriate state of the medium (composition, temperature) and control stimuli.
It should be noted that the definitions of both universal and instance machines are not sharply delimited and in some cases the boundaries between them are rather diffuse.
It is not so difficult to design a reusable instance machine based, for example, on a flow reactor in which nonlinear chemical processes proceed. Moreover, it is possible to change the character of the problem solution after resetting this device by changing the state of the medium or control stimuli. These features are definite steps to universality. Nevertheless, a universal computer is, after reprogramming, the same machine, whereas an instance computer would be more naturally viewed as a different machine (Rambidi 1997).
It should be stressed that the instance machine conception is an important step in understanding the nature of biocomputing. Based on theoretical and experimental investigations performed during the last decade, it presents the further development of Conrad's pioneer guiding principles (Conrad 1985).
The next point important for understanding the essence of the reaction-diffusion means is the neural network architecture of the information processing medium. It is possible to outline a number of structural features that would determine the information processing characteristics of the medium:
-
Cells (figure 4.3), small by comparison with the diffusion length, can be considered as primitive processors representing chemical systems having point-wise kinetics. If these cells are to be considered as independent, trigger and oscillatory regimes should be inherent.

Figure 4.3: Schematic representation of neural network architecture of reaction-diffusion medium.Diffusion length is determined as in Field and Burger (1985):

Here, D is an average diffusion coefficient, and T is a characteristic time of the dynamic process.
In common parlance, the diffusion length is the distance where total intermixing of reaction components has taken place because of diffusion.
-
Cells are coupled because of diffusion. This coupling determines a number of complicated dynamic modes that are displayed in thin layers and in a volume of the medium.
-
Changing the composition and temperature of the medium can provide control of excitable medium regimes. One powerful variant is based on using media containing light-sensitive components. In this case, the composition of the medium can be easily changed by light illumination, with the degree of change being controlled by the amount of light exposure.
-
Generally speaking, each cell is connected to each other cell of the medium due to diffusion coupling. This interaction is carried out with a time delay proportional to the distance between cells, and the strength of the interaction decreases proportionally to this distance.
The above model, representing a system of cells coupled by diffusion, does not take into account that the media are uniform distributed systems. A more adequate model should be invariant to infinitesimal shifts of the cell system along the surface of the medium.
Given these features of reaction-diffusion media, a comparison between the dynamic and information processing characteristics of such media and those of neural networks seems to be of substantial value. The most important points seem to be:
-
How adequate are the responses of excitable media and neural networks to predetermined external excitation?
-
What conclusions can be made about structural characteristics of the media (first, what is the real range of interaction between cells) based on this comparison?
Different approaches to describe such pseudoplanar neural networks with lateral connections are known, starting with the pioneer work by McCulloch and Pitts (1943). A comprehensive review of neural net models offered in the 1970s and 1980s has been done by Grossberg (1988).
In the late 1960s, Pozin (1970) and his coworkers performed a series of investigations based on a neural net model described by the kinetic equation:
![]()
Here, xi is the potential of the ith neuron, F(pi) is a sigmoidal function depending on the algebraic sum of signals coming from outputs of other neurons.
![]()
sij is a function characterizing the coupling of ith and jth neurons, Ii is an input (external stimulus) of ith neuron.
This model (figure 4.4) represents a neural network having sigmoidal feedback, containing both excitatory and inhibitory inputs. More exactly, the distribution of excitatory and inhibitory signals was set by individual coupling functions g(x), depending on the distance between neurons in the network surface. Extended oneor two-dimensional signals acting on the neural network were considered. It was assumed that the dimensions of input signal features were large compared with interneuron distances. Neural networks were therefore considered as continuous homogeneous media.

Figure 4.4: Schemes of neural networks (A) Pozin's feedback network containing excitatory (white circles) and inhibitory (black circles) neurons. (B) Grossberg's shunting on-center off-surround feedback network.
The main result obtained in the investigation (Pozin 1970) was that the signal input (for instance, a rectangular wave) into the neural network could be sharpened or broadened; also that the contour of the signal could be enhanced depending on the shape of the coupling function. (Numerical simulations of these effects performed using techniques in Pozin 1970 are shown in figure 4.5).

Figure 4.5: Responses of a neural network to external excitation calculated based on Pozin's model and representing: broadening of an input image (A), its sharpening (B), and contour enhancement (C). The upper level of the figure shows the shape of an input distribution, responses of the network are shown at the lower level, shapes of g(x) function (see text) are between them.
The simulation represents folding of a rectangular intensity distribution and a function of the form:
![]()
This function depends on four adjustable constants: A1, A2, B1, and B2 (see figure 4.5).
Later, Yakhno and Colleagues (see, for instance, Nuidel and Yakhno 1989; Belliustin et al. 1991) continued this line of investigations and used it for a detailed analysis of image processing operations.
In the late 1960s, Grossberg launched a detailed investigation of neural networks. During the last two decades, Grossberg and his collaborators have analyzed different aspects of neural network activity—the image processing capabilities investigated by Grossberg (Grossberg 1973, 1976, 1988) and Ellias and Grossberg (1975) are mentioned below.
Based on psychobiological and neurobiological data, Grossberg concluded that shunting on-center off-surround feedback networks (see figure 4.4) display a number of remarkable image features.
Neural networks of this type are described by kinetic equations of the type:
![]()
Here, the main notations coincide with notations of equation (4.8):
f(xi) is a feedback nonlinear signal.
Ii and Ji are stimuli acting on excitatory and inhibitory neurons.
Grossberg has shown that shunting on-center off-surround feedback networks posses the key properties of:
-
Solving the noise-saturation dilemma
-
Normalizing or conserving their total activity
-
Being capable of absolutely stable short-time memory
These neural networks proved to be capable of quenching (sharpening) or amplifying (broadening) the noise of input signals, or of enhancing a signal's contour or the most intense fragments depending on the shape of the f(x) function (figure 4.6).
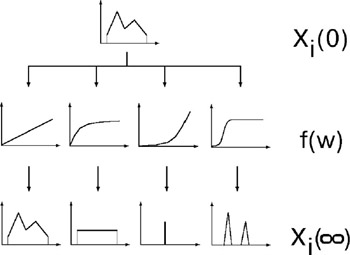
Figure 4.6: Responses of an on-center off-surround feedback neural network to arbitrary chosen external excitation depending on the shapes of f(w) function (see details in text).
Grossberg (1976) has also noted a dynamic analogy between shunting on-center off-surround feedback neural nets and reaction-diffusion systems, which were used by Gierer and Meinhardt (1972) for the description of the process of biological pattern formation. Later, Masterov, Rabinovich, Tolkov, and Yakhno (Masterov et al. 1988) showed the analogy between the reaction-diffusion equations and the neural net integrodifferential equations.
Thus different theoretical considerations show that common information processing capabilities of neural networks and reaction-diffusion media should be primarily manifested in: storing information in short-term memory; and performing such operations as sharpening or broadening input signals and enhancing the contour of an input picture or its most intense fragments.
Given the information processing properties of reaction-diffusion systems, one may picture some realizable versions of such systems. Their structure defines two general types of design solutions, differing in that the levels of information processing may be spatially combined or spatially separated. In spatially combined systems, the successive levels (stages) of information processing are materialized as a set of consecutive dynamic processes (chemical reactions) that proceed in the same volume, the reaction products of some levels being reaction substrates for the following levels. In spatially separated devices, processes of different levels are localized in certain supramolecular domains.
Let us now consider mostly one-level information processing methods. It is easy to construct a variety of devices of different structures using a volume of a liquid Belousov-Zhabotinsky reagent having a preselected shape. It amounts to a threedimensional network of elementary processors combined into a specific integral system. Control of both the system and the input-output of data proved to be, in this case, too complicated a problem. Therefore a pseudo two-dimensional system using a thin layer of Belousov-Zhabotinsky reagent will be discussed below.
Information processing devices with these capabilities can be designed using complex nonlinear media as a basis (Rambidi, Chernavskii, and Krinsky 1993).
Construction of biomolecular information processing devices is a problem of great complexity because of tremendous technical and material difficulties. Prior simulation of information processing capabilities therefore proves to be urgent to avoid useless, costly, and laborious attempts.
Theoretical methods are powerful tools for the investigation of nonlinear biomolecular system dynamics. Nevertheless, it often happens that commonly used mathematical models do not prove to be fully adequate to mimic processes under investigation because of the high structural and dynamic complexity of the system. Moreover, these models lead often to immense difficulties in analytical handling of the equations describing the model and to cumbersome numerical calculations.
One of the most straightforward ways to simulate information processing primitive operations of biomolecular devices based on complex nonlinear dynamics is via experimental modeling. In this case, Belousov-Zhabotinsky-type excitable media are promising tools because of the close similarity between the dynamics of these media and those of known biomolecular systems.
|
- ERP Systems Impact on Organizations
- Challenging the Unpredictable: Changeable Order Management Systems
- Enterprise Application Integration: New Solutions for a Solved Problem or a Challenging Research Field?
- The Effects of an Enterprise Resource Planning System (ERP) Implementation on Job Characteristics – A Study using the Hackman and Oldham Job Characteristics Model
- Relevance and Micro-Relevance for the Professional as Determinants of IT-Diffusion and IT-Use in Healthcare
- Chapter I e-Search: A Conceptual Framework of Online Consumer Behavior
- Chapter II Information Search on the Internet: A Causal Model
- Chapter VII Objective and Perceived Complexity and Their Impacts on Internet Communication
- Chapter XII Web Design and E-Commerce
- Chapter XVIII Web Systems Design, Litigation, and Online Consumer Behavior