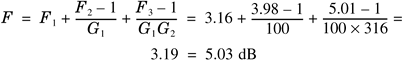5.5 Noise Level

The performance of an indoor radio frequency transmission system is determined by the received signal strength and the noise floor. To compute equivalent noise floor at the input of a receiver, it is necessary to know the gains or losses at different receiver stages and the receiver antenna ambient noise temperature.

5.5.1 Antenna Ambient Noise Temperature

It is critical to know the noise level at the very front end of a receiver because the signal-to-noise ratio determined there cannot be further improved by subsequent electronics. For wired communication systems, the minimum noise level is determined by the thermal temperature of electronic components at the very front end. Sometimes the noise level of the environment could be higher than the receiver front end thermal noise level. For the indoor radio frequency channel, the similar logic of noise level determination applies except the noise level of the environment is related to the antenna ambient noise temperature. The ambient noise temperature is measured for the radio environment where the antenna is located and can be higher or lower than the temperature of the antenna. This situation is similar to that of the environment noise level, which can be higher or lower than the wired communication system. The receiver front-end noise level for the indoor radio frequency environment is determined by the higher of either environment or antenna temperature. For the indoor radio frequency environment, this usually is the room temperature which is between 17 and 27°C, 63 and 75°F, or 290 and 300°K. The noise power at a particular temperature is expressed by

Equation 5.46

where k is the Bolzmann's constant, T₀ is the ambient temperature, and B is the bandwidth. The noise level can also be expressed in terms of voltage by

Equation 5.47

where R is the antenna impedance.

For k = 1.37 x 10^-23 , T₀ = 294°K, and B = 10⁶Hz, the noise power is calculated by

Equation 5.48

The corresponding power density level is P_n/B = 1.37 x 10 ²³ x 294 = 4.03 x 10 ²¹ = 173 dBm/Hz.

5.5.2 Receiver Noise Figure

When a signal passes through an electronic component, either an active device with gain or a passive device with loss, additional noise level will be introduced, and the net signal-to-noise ratio will be reduced. For a unit gain device, the ratio of output noise power to input noise power is defined as the noise figure, which can be expressed in terms of ratio or decibels:

Equation 5.49

For an active device with gain , the noise figure is defined by

Equation 5.50

Equation 5.50 also applies to a passive device with loss where G will be smaller than unity in terms of ratio or negative in terms of decibels. If input and output noise levels are similar because of the ambient temperature for a passive device, the loss of the passive device becomes the noise figure as illustrated by

Equation 5.51

5.5.3 Equivalent Noise Floor

A transceiver used in an indoor radio frequency communication system usually consists of many stages of different gains and noise figures. The noise figure of the first stage is dominant while the effects of noise figures in the following stages are reduced by the accumulative gains of previous stages. Specifically, the noise figure of the receiver is related to noise figures of individual stages as shown by

Equation 5.52

The equivalent noise temperature is related to the antenna ambient temperature and the receiver noise figure as shown by

Equation 5.53

If we have a receiver consisting of three stages with F₁ = 5 db, F₂ = 6 dB, F₃ = 7 dB, G₁ = 20 dB, G₂ = 25 dB, and G₃ = 15 dB, the system noise figure is calculated as

Equation 5.54

Notice again that the front-end noise figure is dominant. With an antenna ambient temperature of 68°F, or 294°F, the equivalent noise temperature is calculated by

Equation 5.55

The corresponding noise power density level is calculated by

Equation 5.56

When the temperature rise T₀ = 299°K, the equivalent temperature becomes T_e = 2.19 x 299°F = 654.81°F. The noise power density will reach the following level:

Equation 5.57