Detection Using Math
| As you just saw, using the hitTest() method is pretty painless. I've already hinted that creating collision-detection scripts based on math is more difficult than that. So this is probably an appropriate time to tell you what makes this type of collision detection so much better than attempting to use hitTest() for all your collision-detection needs. Let's start by listing the limitations of hitTest(). Object-shape restrictions. As you saw earlier in this chapter, the hitTest() method only works with the bounding box of a movie clip, or a point and the shape within that movie clip. How would you detect collisions between two pool balls, or between a ball and an angled line? With hitTest(), the collision detection for those situations would not be accurate, because it doesn't handle collision detection between the shapes within two movie clips. Using math, we can create collision-detection scripts for many shapes. Inhibited code-graphics independence. This concept can be tough to grasp. In all of the examples given so far in this book, we have updated the position of a movie clip on the screen by grabbing its current position, adding to it, and then changing the position of that movie clip. It is better practice to keep track of where objects on the screen should be in code. For instance, you could have a variable that stores the x position of the ball. When it is time to update the position of the ball with the x velocity, you would add to the variable that stores the x position, and then set the position of the clip on the screen from that variable. This is useful because we can detect a collision before setting the position of the movie clip on the stage. With hitTest(), the object must be physically moved on the screen, and then the collision detection is based on the overlap of two graphical elements. We will be using code-graphics independence throughout the rest of the chapter. Frame-rate dependence. This limitation is related to the one above. Imagine a game of Pong: There is a paddle that's 10 units wide on the left side of the screen. The ball, also 10 units wide, is moving toward the paddle with an x speed of 30 units per frame. It is possible for the ball to be on the right side of the paddle on one frame and to appear on the other side of the paddle on the next frame. With hitTest(), no collision would have been detected because the two clips must overlap during a frame (or within a frame for those of you more comfortable thinking of frames in terms of physical space rather than time duration). It is not smart enough to know that the ball went through the paddle. Using math, we can tell if a collision took place in between frames. Collision was not detected because of the "snapshot" nature of frames.
To recap, using math for collision detection will allow you to:
What follows is a description, with examples, of how to think about and script collision detection between various types of shapes. For some of these we extend the detection script so that it works independently of the frames, and for some we do not.
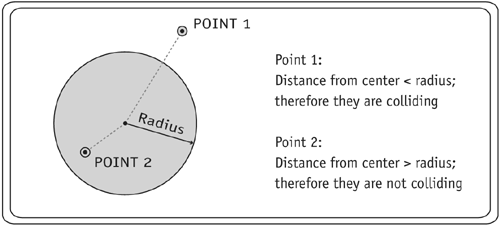
Point-Circle Collision DetectionWe begin the examples of mathematical collision detection with one of the simpler types. A good example of where we might use point-circle collision detection is a dart game. The dart's tip is the point, and the target is made up of a series of concentric circles.
So how do we determine if a point and a circle are colliding? Imagine that you have two movie clips: a circle and a dot (the point). Assume the registration point of the circle movie clip is at the actual center of the circle. Since the point and the circle are movie clips, you can easily find the positions of both. Also, using the distance equation developed in Chapter 3, "Trigonometry 101" (and listed below in ActionScript), we know we can find the distance between the point and the circle. With this information we can write the one condition that determines if a collision is taking place: If the distance between the point and the center of the circle is less than the radius of the circle, then the point is colliding with the circle.
1 //Define point 1 2 point1 = {}; 3 point1.x = point_clip1._x; 4 point1.y = point_clip1._y; 5 //Define point 2 6 point2 = {}; 7 point2.x = point_clip2._x; 8 point2.y = point_clip2._y; 9 //Define circle 1 10 circle1 = {}; 11 circle1.x = circle_clip1._x; 12 circle1.y = circle_clip1._y; 13 circle1.radius = circle_clip1._width/2; What is being done with the ActionScript here is very important, and is similar to what is going to be used for most games and examples given in this book. We create an object for each movie clip. An object (of type object), when first created, is nothing more than an empty storage device. This can be likened to a file cabinet. When you first build (or buy) a file cabinet, it is empty. You then use it to store information about certain things, like your car or house. Unlike a file cabinet, an object object is not a visual or tactile thing it is data stored in memory. Storing information in this fashion is a good practice because it removes the data from the interface. This separation allows you to add or remove movie clips from the stage without losing the data stored in the object. Later you can reassociate the object with another movie clip.
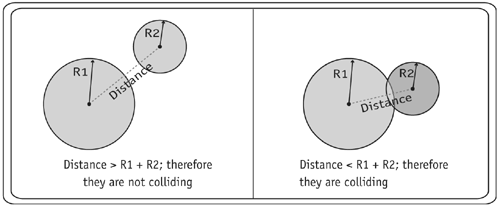
In future scripts within the book, these objects will contain many other things, such as the properties of the object. For example, in the case of a pool ball, the object would contain the ball's color. Some programmers choose to use the movie clip itself as the object to store this information. In some cases that would be OK, but in others for instance, where a movie clip may not always be on the stage it is not a good idea. Imagine a game in which an enemy character is coming after you. This enemy may leave the screen for more ammo and then come back in 30 seconds or so. In this case it is probably a good idea to remove the movie clip from the stage (for performance reasons) but retain the object that stores the enemy's characteristics so we don't have to start "rebuilding" the enemy from scratch. In line 2 of the ActionScript above we create a new object, called point1, that we intend to use as a storage container for information about the point_clip1 movie clip. The action point1={} is shorthand for creating a new empty object and giving it a name. (The long-winded way is point1 = new Object(), so you can see why we'd like the shorthand.) In lines 3 and 4 we simply create variables on the object to represent the position of the point_clip1 movie clip. Lines 5 8 create an object for point_clip2 and store information about it in the same way as the point1 object does. Next, an object is created to store the information about the circle_clip1 movie clip. It stores the x and y positions of the movie clip as well as its radius. The rest of the ActionScript defines the collision-detection function and uses it to test for collisions. 1 //Build collision detection function 2 function pointToCircleDetection(point, circle) { 3 var xDiff = circle.x-point.x; 4 var yDiff = circle.y-point.y; 5 var distance = Math.sqrt(xDiff*xDiff+yDiff*yDiff); 6 if (distance<=circle.radius) { 7 trace("Collision detected!!"); 8 } else { 9 trace("No collision detected."); 10 } 11 } 12 //Check for a collision between point1 and circle1 13 pointToCircleDetection(point1, circle1); 14 //Check for a collision between point2 and circle2 15 pointToCircleDetection(point2, circle1); First we define a function named pointToCircleDetection that accepts two parameters: point and circle. Both point and circle are objects passed in when the function is called. To detect a collision, as we spelled out earlier, we have to compare the distance between the point and the circle with the radius of the circle. To make this comparison, we must determine the distance using the Pythagorean theorem (the method shown back in Chapter 3, "Trigonometry 101"). Lines 3 5 show this. In line 6 we compare the distance with the radius of the circle, and if the distance is less than or equal to the radius, we execute a trace action to inform us that a collision has been detected. If this condition is not met, then a trace action is executed to inform us that no collision has occurred. In lines 13 and 15 we call the detection function while passing in objects whose collision we would like to check. For instance, in line 13 we pass in point1 and circle1. The script will then check for a collision between point1 and circle1. When you generate a SWF movie, you should see two traces in your output window. The first collision detection detected a collision, the second did not. Circle-Circle Collision DetectionIn this section we discuss the logic and scripts needed to determine if two circles are colliding. We will cover this for both frame-dependent and frame-independent situations. By frame dependence, we mean that in every frame we check for a collision, based on where the objects are now (this is like taking snapshots in time). With frame independence, in every frame we check to see if a collision has happened at some point between the last frame and the current frame. The frame-dependent collision detection for two circles is a simple extension of the point-circle collision-detection technique. The frame-independent collision detection for two circles involves a lot more logic and math. Let's look at the easy one first. Frame Dependent Circle-Circle DetectionHere's our case of frame-dependent circle-circle collision detection: If the distance between two circles is less than or equal to the sum of their radii, then a collision is occurring.
As with the point-circle collision detection, we store information about each movie clip in an object. Here is the ActionScript that does this: 1 //Define object for the first circle 2 circle1 = {}; 3 circle1.clip = circle_clip1; 4 circle1.x = circle1.clip._x; 5 circle1.y = circle1.clip._y; 6 circle1.radius = circle1.clip._width/2; 7 circle1.xmov = 3; 8 circle1.ymov = 1; 9 //Define object for the second circle 10 circle2 = {}; 11 circle2.clip = circle_clip2; 12 circle2.x = circle2.clip._x; 13 circle2.y = circle2.clip._y; 14 circle2.radius = circle2.clip._width/2; 15 circle2.xmov = -1; 16 circle2.ymov = 0; First, an object called circle1 is created to store the information about circle_clip1. In line 3 you may notice something you haven't seen before. We are creating a reference to the movie clip with a name of clip in the object itself. Doing this allows us to point to the movie clip using this new reference. For instance, the action circle1.clip._x = 100 would move the x position of circle_clip1 to 100. (I'm going to use this technique of creating references to movie clips frequently throughout the book.) The next three lines create variables to store the circle's position and radius. In lines 7 and 8, we assign an x speed and a y speed to the circle. Lines 9 16 do for circle_clip2 what the first eight lines of ActionScript did for circle_clip1. Next in the ActionScript, we create a function called moveCircles. This function updates the positions of the circles based on their speeds. 1 function moveCircles() { 2 for (var i=1; i<=2; ++i) { 3 var circle = this["circle"+i]; 4 circle.x += circle.xmov; 5 circle.y += circle.ymov; 6 circle.clip._x = circle.x; 7 circle.clip._y = circle.y; 8 } 9 } In this function, there is a for loop that loops through and moves each circle. This ActionScript is not unfamiliar (see balloon_pop_many.fla), although this is the first time we have used the movie-clip reference from an object. Remember that we are storing references to circle_clip1 and circle_clip2 as the clip variable on both the circle1 and circle2 objects, which is where we use them. In lines 6 and 7 you can see that the circles are moved by using the movie-clip reference clip that exists on each object. The function that detects collisions between the circles is called CircleToCircleDetection. It is almost exactly the same as the collision-detection script used in the point-circle collision-detection script. 1 function CircleToCircleDetection(circle_a, circle_b) { 2 var xDiff = circle_a.x-circle_b.x; 3 var yDiff = circle_a.y-circle_b.y; 4 var distance = Math.sqrt(xDiff*xDiff+yDiff*yDiff); 5 if (distance<=circle_a.radius+circle_b.radius) { 6 trace("Collision detected!!"); 7 } 8 } The CircleToCircleDetection function accepts two parameters, circle_a and circle_b. First the ActionScript finds the distance between those two movie clips. Then it reaches a conditional, which checks to see if the distance between the circles is less than or equal to the sum of their radii. If it is, then it executes a trace action. Finally, it creates an onEnterFrame event that calls the moveCircles function and CircleToCircleDetection function in every frame (I'm just mentioning this to wrap up the script; you won't see this event in the code above). Generate a SWF to see it work. Frame Independent Circle-Circle DetectionOK, that was the easy one! Now it's time to talk about frame-independent circle-circle collision detection. The math in this gets a little tough, so before continuing I would like to recap why it's important for you to slog through this. With all of the collision-detection scripts created so far, Flash checks one time per frame to see if there is a collision right now. You can think of this as being like taking snapshots in time. I am sure you can imagine that if an object is moving fast enough, then in one frame it is on one side of an object, and in the next frame it is on the other side of the object. The collision-detection method we've been using wouldn't be able to detect that kind of collision, since as far as it is concerned, a collision never happened. But with the way I'm about to introduce, we can tell (no matter how fast the object is going) if there was a collision between the previous frame and the current frame. This script has direct application to games like pool, pinball, air hockey, miniature golf, or indeed any game in which two balls (circles) can collide. Let's discuss the logic needed for frame-independent collision detection. First, it is important to realize that we can still only check for a collision every frame we can't check in between frames. What we will cover here is how to tell if a collision should have happened in between frames. In Chapter 4, "Basic Physics," we introduced the equations for position and velocity. In Chapter 3, "Trigonometry 101," we introduced how to get the distance between two points. If we know the x and y speeds of each circle (which we do), then we can write equations that specify the x position and y positions of each circle. With these position equations, we can write an equation that determines the distance between the two circles. This leaves us with an equation for the distance between the two circles that is dependent on one variable time (well, OK, for us it's really frames). If we wanted to, we could stick any time into this equation and find the distance that the circles would be apart at that time. Likewise, we could insert a distance, and then solve for the time during which the two circles would be this distance apart. It is the latter example that we are interested in now. The same main condition must be met for the two circles to be colliding: The distance between the two circles must be less than or equal to the sum of their radii. So this is what we do:
Let's look at this in math form before touching the ActionScript.
Here is the ActionScript that defines the objects: 1 game = {}; 2 game.numBalls = 2; 3 for (var i=1; i<=game.numBalls; ++i) { 4 var name = "ball"+i; 5 game[name] = {}; 6 game[name].clip = _root[name]; 7 game[name].xpos = game[name].clip._x; 8 game[name].ypos = game[name].clip._y; 9 game[name].radius = game[name].clip._width/2; 10 game[name].xmov = 0; 11 game[name].ymov = 0; 12 } 13 game.ball1.xmov = 1; 14 game.ball1.ymov = 2; 15 game.ball2.ymov = 1; First we create an object called game. This object will store all of the other objects we create. The only reason for having this container object, game, is to keep from polluting the timeline with unneeded data. We can keep track of everything we need to about the balls in the game object. In the second line we set a variable on the game object that stores the number of balls we have chosen to use. Next, we loop for each ball, create an object for it, and store information about that ball in its object. Notice that we are giving the balls no starting speeds. In lines 13 15 we assign starting velocities to the balls. Then comes the following ActionScript: 1 function moveBalls() { 2 for (var i=1; i<=game.numBalls; ++i) { 3 var ob = game["ball"+i]; 4 ob.tempx = ob.xpos+ob.xmov; 5 ob.tempy = ob.ypos+ob.ymov; 6 } 7 } This function loops through the list of balls (in this case, just two) and updates their temporary positions in memory to their current positions plus their speed. We do not yet update the position of the actual movie clip on the stage. I encourage you to get into this habit of creating a temporary position of the movie clip in memory, because when we start dealing with collision reactions, we will update the temporary position of the movie clip (due to multiple collisions or forces) possibly several times before we actually place the movie clip on the stage. Let's analyze an example. Imagine that you are coding a game in which a ball bounces off a wall. This ball may be moving very fast. Now imagine that on one frame the ball is not colliding with the wall, and on the next frame you detect that half of the ball is colliding with the wall. When this happens, you do not want to update that ball's position on the stage to show this. Rather, it is a good idea to update its position in memory to reflect where the ball should be and then render the ball on the screen. So, if it is detected that the ball is colliding with the wall (no matter how deep into the wall the ball is), then we should update the ball's position in memory so that the ball is just barely touching the wall. At the end of the frame, we render the ball on the screen, and it looks as if it is just barely touching the wall (which is what we want). In real life, a ball would not move past the wall boundary. Next we create a function to render the balls onto the stage. 1 function renderBalls() { 2 for (var i=1; i<=game.numBalls; ++i) { 3 var ob = game["ball"+i]; 4 ob.xpos = ob.tempx; 5 ob.ypos = ob.tempy; 6 ob.clip._x = ob.xpos; 7 ob.clip._y = ob.ypos; 8 } 9 } This function simply sets the physical position of each movie clip using the value of the x and y position variables on the object, which are xpos and ypos. Now (drum roll, please) we come to the function that handles the collision detection itself. It's a fairly large function, but it follows exactly what we discussed about the logic for determining the collisions. 1 function ballToBallDetection(b1, b2) { 2 //set the speed variables 3 var xmov1 = b1.xmov; 4 var ymov1 = b1.ymov; 5 var xmov2 = b2.xmov; 6 var ymov2 = b2.ymov; 7 //set the position variables 8 var xl1 = b1.xpos; 9 var yl1 = b1.ypos; 10 var xl2 = b2.xpos; 11 var yl2 = b2.ypos; 12 //define the constants 13 var R = b1.radius+b2.radius; 14 var a = -2*xmov1*xmov2+xmov1*xmov1+xmov2*xmov2; 15 var b = -2*xl1*xmov2-2*xl2*xmov1+2*xl1*xmov1+2*xl2*xmov2; 16 var c = -2*xl1*xl2+xl1*xl1+xl2*xl2; 17 var d = -2*ymov1*ymov2+ymov1*ymov1+ymov2*ymov2; 18 var e = -2*yl1*ymov2-2*yl2*ymov1+2*yl1*ymov1+2*yl2*ymov2; 19 var f = -2*yl1*yl2+yl1*yl1+yl2*yl2; 20 var g = a+d; 21 var h = b+e; 22 var k = c+f-R*R; 23 //solve the quadratic equation 24 var sqRoot = Math.sqrt(h*h-4*g*k); 25 var t1 = (-h+sqRoot)/(2*g); 26 var t2 = (-h-sqRoot)/(2*g); 27 if (t1>0 && t1<=1) { 28 var whatTime = t1; 29 var ballsCollided = true; 30 } 31 if (t2>0 && t2<=1) { 32 if (whatTime == null || t2<t1) { 33 var whatTime = t2; 34 var ballsCollided = true; 35 } 36 } 37 if (ballsCollided) { 38 //Collision has happened, so throw a trace 39 trace("Ouch!"); 40 } 41 } First we give the function a name, ballToBallDetection, and set two parameters, b1 and b2. When this function is called, the two objects will be passed in and represented by b1 and b2. In lines 2 11 we define the speed and position variables needed. Next, we define all of the constants in terms of the speed and position variables. The variable names match what we discussed earlier in this section. With lines 24 26 we solve the quadratic equation. In line 24 we set a variable called sqRoot whose value is equal to the square-root term in our solution to the quadratic equation (remember that there are two solutions, both of which contain the same square-root term). We set this as a variable so that it can be reused for both solutions (lines 25 and 26). At this point, we have two times at which the balls will collide. What follows in the ActionScript (lines 27 36) is logic to determine if the time was in the past, the present, or the future. If the time is in the past or the present, then it is less than or equal to 1, and a collision has occurred. If the time is in the future (greater than 1), no collision has occurred. If a collision has occurred, then we store the time at which this collision happened (using the whatTime variable). We will use this information in Chapter 6, "Collision Reactions." Also, when a collision is detected, a variable called ballsCollided is set to true. When ballsCollided is true, a final if statement executes a trace action to let you know that a collision was detected. Generate a SWF to see this work. With this collision-detection script, you can determine when in the future a collision may happen. When you solve the quadratic equation for time1 and time2, it tells you any time in the future when the balls will intersect, even if it is a million frames into the future. Looking more than one frame into the future is something I have not yet found a need for, but should a use come for it, we'll know how to do it! Line-Line Collision DetectionIn this section we will discuss the equations for lines and for line segments, and how to tell when lines are intersecting. I have never encountered a situation in which I needed a collision-detection script for two moving lines, so we will just cover detection for two stationary lines. It may not be immediately obvious to you how or where this type of collision detection might come in handy. As an active member of many Flash user boards on the Internet, I frequently see the question of how to tell if two lines are intersecting. The most important application of this that we will see is in circle-line collision detection. One step in the process of detecting the collision of a circle and a line is to test to see if two lines are intersecting.
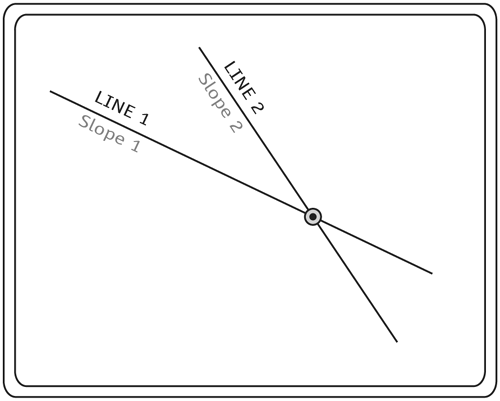
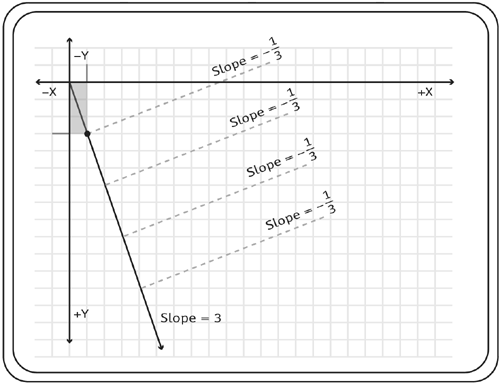
The Equation of a LineTime once again to think back to your high school math class. You may remember this equation: y = m*x+b where m is the slope of the line, and b is the y intercept (the spot where the line intersects the y-axis). This is the equation for a straight line. The slope, m, is defined as the rise over the run of the line. For instance, if the line is at a 45° angle, then the rise of the line equals the run, so the slope is 1. If you have a line that is closer to horizontal, then its rise is less than the run, and therefore the slope is small far less than 1. If the line is exactly horizontal, then the rise is 0, and therefore the slope is also 0.
If you know the slope and y intercept of a line, then you can draw that line. Open draw_line.fla in the Chapter05 directory on the CD. You'll notice that there are no movie clips in this file. The ActionScript it contains builds an object that represents the properties of a line (its slope and y intercept) and then draws the line using two functions. Here are the first few lines of ActionScript in this file, which are used to build the object. 1 _root.createEmptyMovieClip("clip", 1); 2 clip.lineStyle(0, 0x000000, 100); 3 line1 = {}; 4 line1.m = 1; 5 line1.b = 100; In the first line we simply create an empty movie clip on the stage. The line that will be drawn using this ActionScript will be drawn in this movie clip.
In line 2 we specify a line style for the movie clip. Before anything can be drawn in the movie clip, we have to inform Flash of how we would like it drawn. This method tells the movie clip that we want the line to be a hairline (which is a thickness of 0), the color to be black (which has a hex value of 0x000000), and the alpha value to be 100.
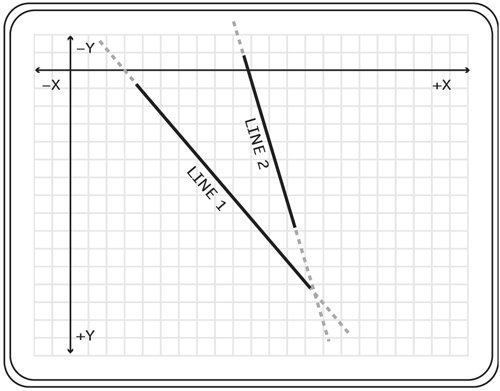
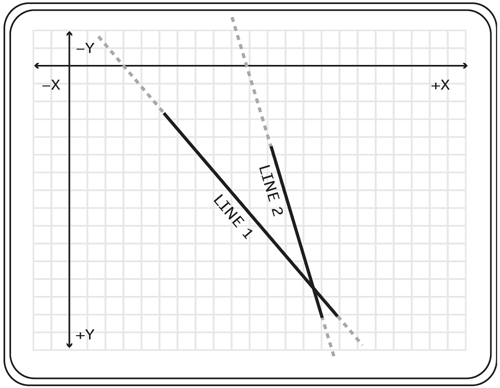
Lines 3 5 create an object called line1 that holds the variables m (for the slope of the line) and b (for the y intercept). Next, we write two functions that work together to draw the line. 1 function findY(line, x) { 2 var y = line.m*x+line.b; 3 return y; 4 } 5 function drawLine(line) { 6 //Choose an x 7 var x = 300; 8 //Find the y 9 var y = findY(line, x); 10 //Move the pen 11 clip.moveTo(x, y); 12 //Choose another x 13 var x = 0; 14 //Find the y 15 var y = findY(line, x); 16 //Draw line 17 clip.lineTo(x, y); 18 } 19 drawLine(line1); The function findY() was created to calculate the y position from the line object passed in and the x position (using the equation for the line y = m*x+b). After that, starting on line 5, we use the drawLine() function. You need two points to draw a line, of course, and so this function chooses two x positions, finds the appropriate y positions from those, and draws a line between this pair of points. On line 11 you see the moveTo() method. This method is used to move the starting position of the Flash "pen" to the coordinates passed in. (The Flash pen, sometimes called the virtual pen, is a place that you cannot see, with the coordinates (0,0), where Flash will start drawing if you were to call the drawing methods. The moveTo() method only moves the position of the pen it draws no lines. There is a method called lineTo(), found in line 17, that handles drawing the line. It draws a line from the current pen position to the coordinates passed in. The final line is what calls the function. This function call passes in a line1 object reference to the drawLine() function. The drawLine() function then uses this reference to access information on the object. It is important to note that all lines are infinite in length, although in this case we are showing only a portion of the line in question. A portion of a line is called a line segment. Intersecting LinesAll lines that are not parallel to each other intersect at some point, and any two lines that have the same slope are parallel. So, to tell if two lines intersect, you simply compare their slopes. If the slopes are not equal, then they do intersect somewhere in space. In this section, we're going to learn how to find out at what coordinates any two lines intersect. Slope 1
First, let's look for the point of intersection. Say we have two lines whose equations are y = m1*x+b1 and y = m2*x+b2 At the point where these two lines intersect, the y value (in the equations above) is the same, and the x (in the equations above) is the same. With this knowledge, we set the two equations equal and write: m1*x+b1 = m2*x+b2 and we solve for x to get: x = (b2-b1)/(m1-m2) This is the x position at which the lines intersect. To find the y position, simply stick this x value back into either of the two line equations (I've chosen the first): y = m1*x+b1
1 function findIntersection(line_a, line_b) { 2 var x = (line_b.b-line_a.b)/(line_a.m-line_b.m); 3 var y = line_a.m*x+line_a.b; 4 dot._x = x; 5 dot._y = y; 6 } This function accepts two parameters, line_a and line_b, which are references to line objects. It then uses the equation we derived above to find the x position of the intersection. Once this x position is found, it is plugged into the equation for the line represented by the line_a object to find the y position. Then the dot movie clip is placed on the stage using these two values. When you test the movie, you will see that the dot appears over the intersection of the two lines. Determining If Two Line Segments Are IntersectingThis is an easy extension of what we have already accomplished in this section. The technique we just introduced allows us to determine if two lines are intersecting. To do this, we find the coordinates of the intersection between these lines as if they were not segments, and then check to see if this point falls within the boundaries of each segment. It may not be obvious when something like this would be useful. Without thinking very hard, I can only come up with one common use, but it's a big one. It occurs when detecting a frame-independent collision between a circle and a line. This is covered in detail in the next section. Lines intersect, but the segments do not; therefore there is no collision
Lines intersect, and so do the segments; therefore a collision is occurring
1 function drawLine(line) { 2 //Choose an x 3 var x = line.x1; 4 //Find the y 5 var y = findY(line, x); 6 line.y1 = y; 7 //Move the pen 8 clip.moveTo(x, y); 9 //Choose another x 10 var x = line.x2; 11 //Find the y 12 var y = findY(line, x); 13 line.y2 = y; 14 //Draw line 15 clip.lineTo(x, y); 16 } In this function we move the pen to one boundary and then draw a line to the other boundary. The result is a visual representation of the line segment. After this function is called, the line object contains the x and y coordinates for both of the line-segment boundaries. Before this function is called, the line object only contains the x1 and x2 line boundaries. The y1 and y2 boundaries are calculated in this function, on lines 5 and 12, and then stored on the line object in lines 6 and 13. The findIntersection() function also has a major addition for our current purposes it now checks the point of intersection to see if it is within the segment boundaries on both lines. Here is the function: 1 function findIntersection(line_a, line_b) { 2 var x = (line_b.b-line_a.b)/(line_a.m-line_b.m); 3 var y = line_a.m*x+line_a.b; 4 dot._x = x; 5 dot._y = y; 6 if ((x>=line_a.x1 && x<=line_a.x2) The first five lines of this function are identical to the findIntersection() function in the previous example. What follows in the remainder of the function are conditional statements that check to see if the intersection point is within the boundaries of the segments. Lines 6 8 check to see if the point is between the x boundaries or between the y boundaries of line_a. If it is, then the point lies on the segment. Lines 9 11 do the same thing as 6 8, but for line_b. If the point lies within the boundaries of both segments, then a trace action is executed, letting you know that an intersection has been encountered.
If you are really interested in point-line collisions, pay special attention to the final scripts developed in the next section. Using them, you'll be able to set the radius of a circle to 0, and thereby detect point-line collisions (a circle of radius 0 is a point). Circle-Line Collision DetectionIn this section we discuss frame-independent circle-line collision detection. This operation has direct application to any game that involves a ball bouncing off (or rolling down) a banked wall or hill games like pinball and miniature golf. We begin by discussing the logic needed to detect a collision between a circle and a line. We are assuming that the line is stationary and the circle is moving. We are also assuming that a collision is not yet taking place when detection begins (so if the ball is colliding with the line when the script starts, then the script will fail). In the previous section we developed a way to determine where two lines intersect. We will use that here as well. A ball in motion builds an imaginary line as it moves (its trajectory). We determine where this line of trajectory and the main line intersect. Once this is found, we use trigonometry to figure out the precise spot at which the circle collides with the line. Then we find the point of collision on the line (where the circle touches the line). Finally, we look at the current position of the circle and figure out how long it will take for the circle to reach the collision point. If this result is less than or equal to one frame, then a collision has occurred. To recap, this is the process of frame-independent circle-line collision detection more concisely:
You have already seen how to accomplish what is in steps 1 and 4, in the sections above. So before dissecting an example FLA file, let's look at how to accomplish what is in steps 2 and 3.
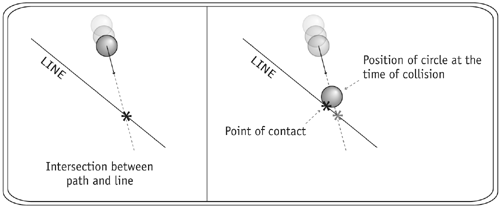
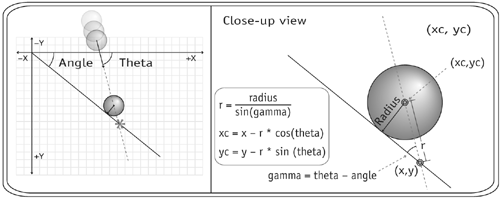
The results of step 1 show us where the path of the circle intersects the line. This intersection point is where the center of the circle would touch the line if it were to make it this far along the path. (After we add collision reactions in the next chapter, the circle will not make it this far; it will have reacted and rebounded when its edge touched the line.) As you can see, this is not the point at which a collision first occurs. If you were to take the circle and slide it backward along its path until only one point intersected with the line, then you would have found the collision point. We can find this point using trigonometry. A right triangle is formed by the radius of the circle; the segment of the circle's path between the line-line intersection and the collision point; and the piece of the line that is between these two intersections. The angle gamma in the image above is the difference between the angle of the path of the ball and the angle of the line. Our goal in this step is to find the position of the circle when it first touches the line. Remember, we're going to find this position by using some trigonometry. Be sure to look at the image above to help you understand the relationships between the values we're using. The length of the path segment, r, is equivalent to radius/sin(gamma). We find this relationship by inspecting the right triangle and using the projection information discussed in Chapter 3, "Trigonometry 101." This relationship tells us the length of that line segment. With that information, we can use trigonometry again to find the position of the circle. The x position of the circle at first collision is the x position of the line intersection of the path and line minus r*cos(theta). And the y position of the circle at the first collision is the y position of the line intersection of the path and the line minus r*sin(theta). (Theta is the angle that the path of the ball makes with the x-axis.) In step 3, we are looking for the actual point where the circle touches the line the point of contact. In the previous step we found the point where the circle is when it touches the line, but not actually the point on the circle that touches the line. To find this point, we must imagine a line drawn from the center of the circle through the point of contact. This is a line perpendicular to the line with which we are colliding. We then find the intersection between these two lines. This point is what we are looking for. We can compare this point with the boundaries of the line segment to determine if the collision happened. There is only one thing we have not discussed in how to create the perpendicular line the equation for that line. We know the equation for the main line (it is stored in the line object), and we know that this new line is perpendicular to the main line. A line perpendicular to another line has a slope that is the negative inverse of it. So if the main line has a slope of 3, then all lines perpendicular to it have a slope of 1/3. All perpendicular lines to this have a slope of 1/3
Now let's look at the getFrame() function. This function does several things:
Steps 3 and 4 are not dependent on each other, and in this function they swap places. Here is the ActionScript for step 1. 1 function getFrames(tempLine, point) { 2 //Step 1 3 var slope2 = point.ymov/point.xmov; 4 if (slope2 == Number.POSITIVE_INFINITY) { 5 var slope2 = 1000000; 6 } else if (slope2 == Number.NEGATIVE_INFINITY) { 7 var slope2 = -1000000; 8 } 9 //The y intercept of the ball trajectory 10 var b2 = point.y-slope2*point.x; 11 //intersection point 12 var x = (b2-tempLine.b)/(tempLine.slope-slope2); 13 var y = tempLine.slope*x+tempLine.b; In this step we search for the intersection between the path of the ball and the line. The slope of the path of the ball is its rise over its run. Notice lines 4 8. If the ball has no speed in the x direction (xmov=0), then the slope is either infinity or infinity. But since our calculations break down at infinity and infinity (and nowhere else), we add some simple conditional logic that sets the slope to either 1,000,000 or 1,000,000 if infinity or infinity, respectively, was detected. (We use 1,000,000 because it is a high enough number that our collision detection will be accurate, but not high enough to make the calculations fail.) Lines 9 13 should look familiar by now they are what determine the intersection between the two lines. Now we move on to the ActionScript for step 2. 1 //Step 2 2 //The angle that the ball is moving 3 var theta = Math.atan2(point.ymov, point.xmov); 4 //The difference between the angle of the line and In this step we want to find out where the ball should be (its x and y positions) when it first collides with the line. We do this by using the trigonometry described earlier. The variable names are the same as described before and match the figure. Lines 10 and 11 give us what we're looking for. We perform step 4 next, before step 3. Here is the ActionScript for this step. 1 //Step 4 2 var dis = Math.sqrt((x-point.x)*(x-point.x) This step is refreshingly short. Here we calculate the number of frames it will take the ball to get from its current position to the point at which it is colliding with the line. Thinking back to the chapter on basic physics, we remember that distance = velocity*frames. If we solve this equation for frames, we get frames = distance/velocity. So if we find the distance between the current position and the collision point, and the velocity along that line, then we can find the number of frames it takes to get there! In line 2 we employ the Pythagorean theorem yet again to obtain the distance. In line 3 we use that same theorem one more time, to find the velocity along the path. Finally, in line 4, we get the number of frames by taking the ratio of distance and velocity.
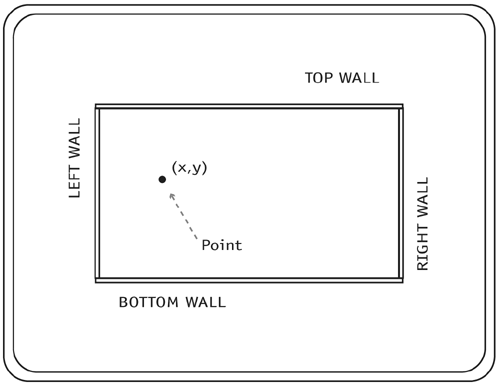
In step 4 we check the physical point of contact to see if it is within the boundaries of the line segment. 1 //Step 3 2 //now check to see if point of contact is on the line To find the coordinates of the point of contact, we imagine a line drawn through the center of the circle and the point of contact. The goal is to find the slope and y intercept of this line (which means we know everything about it) and then, with that information, to see where this line intersects with the main line. This intersection is the point of contact. We know the slope of the main line, and we know that all lines perpendicular to it have a slope that is the negative inverse of its own. Line 3 shows how we find the slope of the imaginary line. Remembering that the equation for a line is y =m*x+b and remembering that we have the coordinates for one point on that line (the center of the circle), we can plug in the x, y, and m (slope) values to find b (the y intercept). Line 4 shows this. Now we have all the information we need about both lines, so we can find the intersection between them. Lines 6 and 7 obtain the coordinates of the line intersection using the technique we have used a few times now. This code block ends with a conditional statement that compares this point (the intersection) with the boundaries of the line segment. If the point falls within the boundaries, then nothing happens. If this point (which is the intersection between the two lines) does not fall within the segment boundaries, then a collision did not happen and so frames is set to 1000 (something high). If the frames variable value is less than or equal to 1 and the point of contact was within the boundaries of the line segment, then the collision is valid. The last line of code above returns the frames variable as the result of the function. The function that called the getFrames() function, bankCollisionDetect(), has the frames returned to it and can then check to see if the frames are less than or equal to 1. We will see this again in the next chapter, Collision Reactions. You are on your way to creating a game with advanced techniques! Point-Rectangle Collision DetectionAfter what you have seen in this chapter so far, what remains is very simple to understand and apply. (We will not be including frame-independent collision-detection scripts in this or the next section.) Since this is not frame-independent collision detection, point-rectangle collision detection is like taking snapshots in time. And if the point is going fast enough, it can move through the rectangle without a collision being detected. The logic for detecting a collision between a point and a rectangle is simple. The position of the point is compared with the position of each wall of the rectangle. If the point's x position is gr?ater than the x position of the left wall and less than the x position of the rectangle's right wall, and the point's y position is greater than the y position of the top wall (remember that the y-axis is inverted in Flash) and less than the y position of the bottom wall, then a collision is occurring.
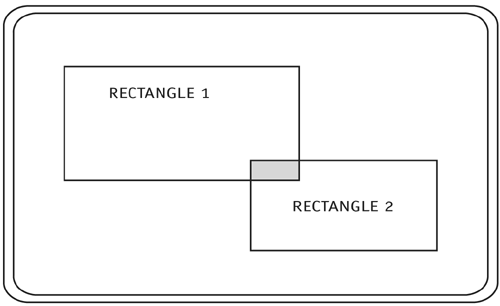
1 //Create an object to store information about point_clip1 2 point1 = {}; 3 point1.clip = point_clip1; 4 point1.x = point1.clip._x; 5 point1.y = point1.clip._y; 6 point1.xmov = 3; 7 point1.ymov = 1; 8 //Create an object to store information about rectangle_clip1 9 rectangle1 = {}; 10 rectangle1.clip = rectangle_clip1; 11 rectangle1.x = rectangle1.clip._x; 12 rectangle1.y = rectangle1.clip._y; 13 rectangle1.width = rectangle1.clip._width; 14 rectangle1.height = rectangle1.clip._height; You have seen this many times by now. We create an object for each movie clip on the stage to store information about that movie clip. Notice that for the rectangle we are storing its position (its registration point is at the upper-left corner) as well as its width and height. Next in the ActionScript are two functions, one for creating a temporary position of the point in memory and the other to position the movie clip on the stage. We will not list these functions here, since they are identical to what we have seen several times already. Here is pointRectangleDetection(), the function that detects collisions between the point and the rectangle. 1 function pointRectangleDetection(point, rectangle) { 2 //position of the point 3 var x = point.x; 4 var y = point.y; 5 //left and right walls 6 var x1 = rectangle.x; 7 var x2 = x1+rectangle.width; 8 //top and bottom walls 9 var y1 = rectangle.y; 10 var y2 = y1+rectangle.height; 11 //check to see if the point is within all of the walls 12 if (x>x1 && x<x2 && y>y1 && y<y2) { 13 trace("Collision Detected!!"); 14 } 15 } This function accepts two parameters, point and rectangle, which are references to two objects. First, two variables are created that represent the position of the point. Then in lines 6 10, the x and y positions of the walls are assigned to variables. Finally, in line 12, a conditional is started that checks to see if the x position of the point is greater than the left wall but less than the right wall, and that the y position of the point is greater than the top wall and less than the bottom wall. If this condition is met, then a collision is occurring, and a trace action is executed. Finally (although this is not shown above), an onEnterFrame event calls getTempPositions(), pointRectangleDetection(), and render() in every frame. Rectangle-Rectangle Collision DetectionLike point-rectangle collision detection, collision detection between two rectangles is easy to perform. Rectangle_a is colliding with rectangle_b if all of the following are true:
They are colliding!
1 function RectangleRectangleDetection(rectangle_a, This function accepts two parameters, rectangle_a and rectangle_b, which are references to objects. In lines 2 14, we set variables to store the positions of the left, right, top, and bottom walls of both rectangles. Then, in line 15, an if statement uses the logic we mentioned above to determine if a collision is taking place. It compares the positions of the walls in rectangle_a with the positions of the walls in rectangle_b. If the condition is met, then the rectangles are colliding and a trace action is executed. |
EAN: N/A
Pages: 163

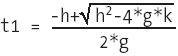 and
and 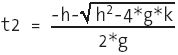


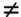 Slope 2; therefore they intersect at some point
Slope 2; therefore they intersect at some point