The Heart of Trig

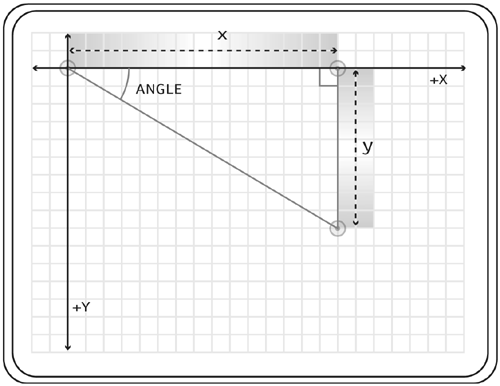
Is it all coming back to you yet? I hope so, because here's where we get to the real inner workings of trigonometry where you can see how it's all going to come together. In this section we will cover the sine, cosine, and tangent functions, as well as projection. With knowledge of these operations under your belt, you will be able to understand the programming concepts you'll encounter in the following chapters (especially Chapter 6, "Collision Reactions").

Sine, Cosine, and Tangent

Sine, cosine, and tangent are known as trigonometric functions. Although what they mean is very simple, many people have trouble understanding them. This conceptual problem happens because it is easy to think that the trigonometric functions give a result by some esoteric or even mystical process. The truth is that these functions just use various ratios of the triangle side lengths to give results. Look at the triangle in the figure below. Notice that we are using x and y instead of a and b to label the side lengths. These are more common side names in programming. Notice the angle in the figure labeled angle.

All three of the trigonometric functions are defined by taking ratios of the sides of this triangle. A trigonometric function takes an angle (in Flash it must be measured in radians) and returns a value. For instance, the sine of 45° is .707. To test this for yourself in Flash, here is an ActionScript code snippet you can write:

 angle=45;  radians=angle*Math.PI/180; trace(Math.sin(radians)); 

Line 1 in the above code block sets the angle in degrees. Line 2 converts degrees to radians, and line 3 computes the sine and displays the result in the output window.

Table 3.1 lists these "big three" functions, their definitions, which methods of the Math object they correspond to in Flash, and a valid value range that can be returned from these functions.

Table 3.1. Trigonometric Functions in Flash

Trigonometric Function	Mathematical Definition	Method in Flash (Angle is in radians)	Minimum Result	Maximum Result
Sine	sin(angle)=y/c	Math.sin(angle)	-1	1
Cosine	cos(angle)=x/c	Math.cos(angle)	-1	1
Tangent	tan(angle)=y/x	Math.tan(angle)	Negative infinity	Positive infinity

It wouldn't hurt to commit some simple results of the trigonometric functions to memory. This can help tremendously when debugging a script. Table 3.2 shows some simple values for you to remember, should you choose to.

Table 3.2. Trigonometric Equivalents

Typical Angles in Degrees	Sine	Cosine	Tangent
0	0	1	0
45	0.707	0.707	1
90	1	0	Infinity
180	0	-1	0

Since you are able to calculate the sine, cosine, and tangent of an angle, it makes sense that there would also be some way to go from a number back to an angle. There is a set of functions for this, called the inverse trigonometric functions: inverse sine, inverse cosine, and inverse tangent. Some people use the term arc (as in arcsine) rather than inverse. Table 3.3 contains a list of the available inverse trigonometric functions.

Table 3.3. Inverse Trigonometric Functions

Inverse Trigonometric Function	Method in Flash	Description
Inverse sine	Math.asin(number)	Returns the angle whose sine is equal to the number
Inverse cosine	Math.acos(number)	Returns the angle whose cosine is equal to the number
Inverse tangent	Math.atan(number)	Returns the angle whose tangent is equal to the number
Inverse tangent2	Math.atan2(y, x)	Returns the angle whose tangent is equal to y/x

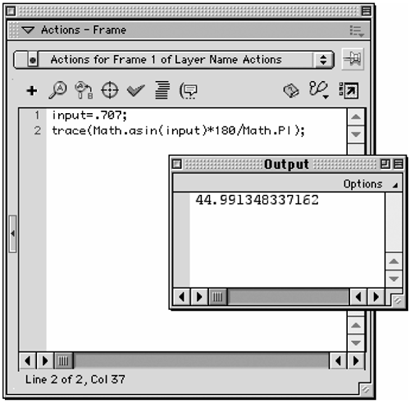
The inverse trigonometric functions take a number as an input parameter and return an angle in radians. To convince yourself of how this works, try this example in Flash:

 input=.707;  trace(Math.asin(input)*180/Math.PI); 

Line 1 sets a variable called input with a value of .707. Line 2 uses the inverse sine method of the Math object (which returns an angle in radians) and then converts it to degrees. The result is traced in the Output window and should be very close to 45°. (It is not exactly 45° because the true sine of 45° has many more decimal places than .707.)

Projection

The word projection in the context of trigonometry means to project a quantity (such as distance or velocity) onto the x-axis and y-axis. Using what you'll learn in this section will help you when building games. For an example of what projection can help you accomplish, open the file shooter.fla in the Chapter03 folder on the CD-ROM. In this file, a ship rotates to point toward your mouse. When you click anywhere on the movie's stage, a projectile fires from the nose of the ship. The velocity of the projectile points toward your mouse (or at least to the place where your mouse was when you clicked it). In order for this movement to be programmed in Flash, the velocity must be projected along the x-axis and y-axis.

The programmatic movement seen in this example file is not covered until Chapter 4, "Basic Physics."

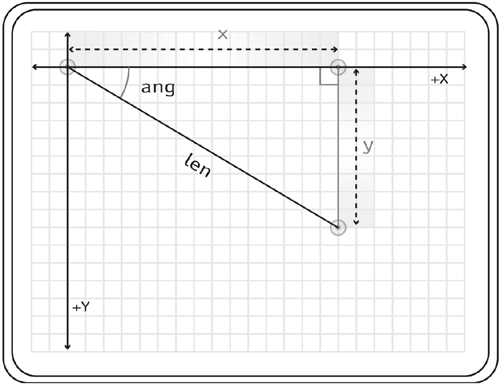
Imagine a diagonal line of length len drawn in Flash at angle ang. A piece of this line extends along the x-axis and another piece of it along the y-axis. If the angle were 0°, then the line would extend only along the x-axis. If the angle were 90° then the line would extend only along the y-axis. With any other angle, the line extends both in the x direction and the y direction. (Put another way, no two coordinates on the line have the same x or y value: A horizontal line always has the same y value for all of its coordinates. A vertical line always has the same x value for all of its coordinates. A diagonal line never repeats an x or y coordinate.) If you were to draw a right triangle from this diagonal line, then the two other sides of that triangle would be the pieces that extend along the x-axis and y-axis.

Finding the length of either (or both) of those pieces by using the values ang and len is called projection. These values are found by using the trigonometric functions that we've already discussed above.

As seen in the previous section:

cos(angle)=x/c

In the example here, angle is replaced with ang and c with len. So:

cos(ang)=x/len

To find the projection of len along the x-axis, we solve for x:

x=len*cos(ang)

Or with ActionScript:

 x=len*Math.cos(ang);  

To find the y projection we use

sin(ang)=y/len

And solve for y:

y=len*sin(ang)

Which converts to this in ActionScript:

 y=len*Math.sin(ang);  

Think of projection like a shadow cast from an object onto the floor or a wall. For the example given in this section, first we would imagine a light source coming from below to cast a shadow on the x-axis. The length of the shadow cast from the line on the x-axis is the same as the projection we would calculate using trigonometry. Next we would imagine a light source coming from far off to the right shining left. The shadow cast on the y-axis is equal to that which we would calculate using trigonometry.