SQRT -- Square Root

SQRT Square Root

The reciprocal and square root are two mathematical operations that have special functionality with vector processors. The division operation is typically performed by multiplying the reciprocal of the denominator by the numerator. A square root is not always just a square root; sometimes it is a reciprocal square root. So first we examine some simple forms of these.

Equation 14-1: Reciprocal

 

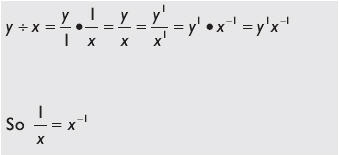
Another way to remember this is:

Equation 14-2: Square root

 

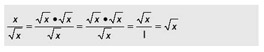
The simplified form of this parallel instruction individually calculates the square root of each of the packed floating-point values, and returns the result in the destination. Some processors support the square root instruction directly, but some processors, such as the 3DNow! instruction set, actually support it indirectly through instructional stages. And some processors support it as a reciprocal square root.

So now I pose a little problem. We hopefully all know that a negative number should never be passed into a square root because computers go BOOM, as they have no idea how to deal with an identity ( i ).

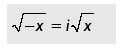
With that in mind, what is wrong with a reciprocal square root? Remember your calculus and limits?

Hint 

As x approaches zero from the right.

Okay, how about this one?

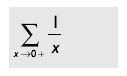
Do you see it now? You cannot divide by zero, as it results in infinity and is mathematically problematic . So what has to be done is to trap for the x being too close to zero (as x approaches zero) and then substitute the value of one as the solution for the reciprocal square root.

 y = (x < 0.0000001) ? 1.0 : (1 / sqrt(x));  // Too close to zero 

It is not perfect but it is a solution. The number is so close to infinity that the result of its product upon another number is negligible. So in essence the result is that other number; thus the multiplicative identity comes to mind: 1 n = n. But how to deal with this in vectors? Well, you just learned the trick in this chapter! Remember the packed comparison? It is just a matter of using masking and bit blending. So in the case of a reciprocal square root, the square root can be easily achieved by merely multiplying the result by the original x value, thus achieving the desired square root. Recall that the square of a square root is the original value.

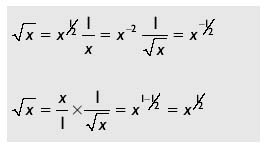
vD[] = (vA[]);

1—SPFP Scalar Square Root

Mnemonic

P

PII

K6

3D!

3Mx+

SSE

SSE2

A64

SSE3

E64T

SQRTSS