14.4 Single-User Throughput

14.4 Single-User Throughput

14.4.1 Single-User Bandwidth Efficiency

We first consider an isolated single-user link limited only by thermal noise. Within the context of a real system, this would correspond to an extreme case wherein the entire system bandwidth is allocated to an individual user. Furthermore, it would require that no other users are active anywhere in the system or that their interference is perfectly suppressed. Clearly, these are unrealistic conditions, and thus the single-user analysis provides simply an upper bound, only a fraction of which is attainable. In addition, this analysis determines what cell sizes can be supported.

With a single transmit and a single receive antenna, the normalized channel is not a matrix but rather a scalar H and the single-user bandwidth efficiency can be expressed as

(14.6)

with expectation over the distribution of H. Implicit in this expectation is the use of interleaving and coding over the small-scale fading fluctuations. ^[31] Shadow fading, however, cannot be similarly averaged out without imposing an unacceptable degree of latency. Thus, with respect to the large-scale variations, we prefer to resort to the idea of outage bandwidth efficiency, which is the value of C supported with certain (high) probability.

When multiple antennas are used at the transmitter or receiver, the bandwidth efficiency can be generalized ^[32] to

(14.7)

with I the identity matrix and with |H|² replaced by HH,^H where ( )^H indicates the Hermitian transpose of a matrix. Although a closed-form solution for Equation 14.7 can be obtained, the corresponding expression is rather involved. ^[33] More insightful expressions can be obtained by making the number of antennas large and, remarkably, such asymptotic expressions can be scaled to yield a very tight approximation to the capacity for any number of antennas. ^[34] Therefore, throughout the rest of this section we shall evaluate these limiting behaviors to gain some insight while illustrating the exact behavior numerically.

14.4.2 Transmit Diversity

A basic downlink strategy based on the deployment of base station arrays only, which has already been incorporated into the 3G roadmap, is that of transmit diversity. In this case, the base station is equipped with n_T uncorrelated antennas, while the terminal is equipped with a single antenna. Thus, the normalized channel H adopts the form of a vector and the single-user bandwidth efficiency becomes

(14.8)

From the law of large numbers, the term ||H||²/n_T converges to unity as the number of transmit antennas grows, ^[35] and thus Equation 14.8 converges to

(14.9)

showing no dependence on the number of antennas. Hence, the bandwidth efficiency saturates rapidly. The single-user throughput achievable with B = 5 MHz as a function of the range is plotted in Figure 14.2 parameterized by the number of transmit antennas. As certified by this figure, there is little advantage in increasing the number of base antennas beyond n_T ≈ 3 to 4, because of the increasingly diminishing returns. The limiting throughput achieved with an infinite number of antennas, corresponding to the bandwidth efficiency in Equation 14.9, is also shown.

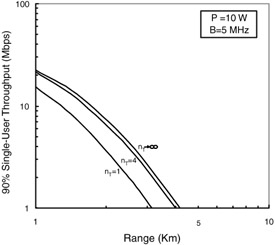
Figure 14.2: Single-user throughput (Mbps) supported in 90 percent of locations vs. range (km), with transmit diversity at the base station and a single omnidirectional antenna at the terminal. n_T is the number of 15-dB uncorrelated antennas at the base. Transmit power P = 10 W; bandwidth B = 5 MHz.

14.4.3 Receive Diversity

The same structure that provides transmit diversity to the downlink enables, by reciprocity, receive diversity for the uplink. The uplink channel H is still a vector, the exact transpose of its downlink counterpart, and the corresponding efficiency is given by

(14.10)

Again, as n_R grows the law of large numbers can be invoked to yield, in the limit

(14.11)

displaying the well-known logarithmic improvement with the number of receive antennas, improvement that is a direct consequence of a progressively higher SINR, as more power is being captured by the additional antennas. Notice that this is in sharp contrast with the transmit diversity case, where the total transmit power is constrained, and thus does not grow with the number of antennas.

Hence, the uplink efficiency does not saturate, but it grows at an increasingly slower pace.

14.4.4 Multiple-Transmit Multiple-receive Architectures

We now turn our attention to MTMR architectures. In this case, the terminal must be equipped with its own array of antennas. For the sake of concreteness, we consider a symmetric scenario with n = n_T = n_R, but similar analysis can be performed for n_T ≠ n_R. As n is driven to infinity, the bandwidth efficiency converges ^[36], ^[37] to

(14.12)

indicating that the bandwidth efficiency grows linearly with the number of (uncorrelated) antennas, which is a key result that contrasts with conventional diversity systems, using multiple antennas at either transmitter or receiver exclusively, wherein the growth is at best logarithmic. The bandwidth efficiency becomes particularly revealing at high SINR, wherein Equation 14.12 particularizes ^[38] to

(14.13)

The attainable throughput in B = 5 MHz as a function of the range is depicted in Figure 14.3, parameterized by the number of transmit and receive antennas. Notice the extraordinary growth in achievable throughput unleashed by the additional signaling dimensions provided by the combined use of multiple transmit and receive antennas. With only n = 8 antennas at both transmitter and receiver, the single-user throughput can be increased by an order of magnitude. Furthermore, the growth does not saturate as long as additional uncorrelated antennas can be incorporated.

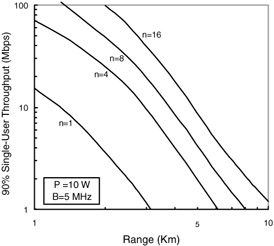
Figure 14.3: Single-user throughput (Mbps) supported in 90 percent of locations vs. range (km) with MTMR technology. n is the number of 15-dB antennas at the base station, as well as the number of omnidirectional antennas at the terminal. Transmit power P = 10 W; bandwidth B = 5 MHz.

^[31]Biglieri, E., Proakis, J., and Shamai, S., Fading channels: information-theoretic and communication aspects, IEEE Trans. Information Theory, 44 (6), 2619–2692, 1998.

^[32]Foschini, G.J. and Gans, M.J., On the limits of wireless communications in a fading environment when using multiple antennas, Wireless Personal Communications, 1998, pp. 315–335.

^[33]Telatar, I.E., Capacity of multiantenna Gaussian channels, Eur. Trans. Telecommun., 10, Nov. 1999, pp. 585–595.

^[34]Lozano, A. and Tulino, A.M., Capacity of multiple-transmit multiple-receive antenna architectures, IEEE Trans. Inf. Theory, 48(12), 3117–3128, Dec. 2002.

^[35]Telatar, I.E., Capacity of multiantenna Gaussian channels, Eur. Trans. Telecommun., 10, Nov. 1999, pp. 585–595.

^[36]Verd , S. and Shamai, S., Spectral efficiency of CDMA with random spreading, IEEE Trans. Inf. Theory, 45, 622–640, 1999.

^[37]Rapajic, P. and Popescu, D., Information capacity of a random signature multiple-input multiple-output channel, IEEE Trans. Commun., 48 (8), 1245–1248, 2000.

^[38]Foschini, G.J. and Gans, M.J., On the limits of wireless communications in a fading environment when using multiple antennas, Wireless Personal Communications, 1998, pp. 315–335.