Hack 60. Estimate Pi by Chance

Statisticians like to think that anything important can be discovered using statistics. That might actually be true, since it turns out that you can use statistics to estimate the value of one of the most important basic values in science: pi.

The ability to calculate pi is one of the routine skills for all budding geniuses. I remember, for example, that dividing 22 by 7 comes pretty close. There are a variety of other ways, some more accurate than others. My favorite method, though, requires the element of chance and a long, lonely sea voyage or other period of enforced solitude. Intrigued? Read on, Gilligan.

Before showing how to estimate the value of pi, I'll begin our discussion by presenting a couple of basic facts from geometry. Don't panic; I don't know much about geometry, so we won't spend a lot of time on this. I'll just cover the basics we need to appreciate the magic of this hack.

Pi

In geometry, key relationships have been found between pi, a number that is roughly 3.14159 (symbolized byp), and the way various parts of a circle fit together, as shown in Figure 5-6.

Figure 5-6. Calculating pi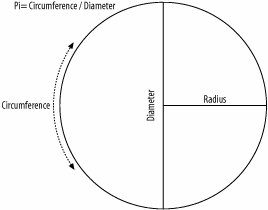

For example, if you take the diameter of a circle and multiply it by pi, you will get the circumference of the circle. If you take the radius of a circle, square it, and multiply that value by pi, you will get the circle's area.

All pretty cool, perhaps, but it is primarily of interest to those who like to play with geometry, not with statistics. But just wait.

Pi and Falling Needles

In the 1700s, Georges-Louis Leclerc presented a half-geometry/half-statistics puzzle to the world. He was the Count of Buffon, or something, so this problem is known as Buffon's Needle Problem. He presented it generally, without specifics, and I summarize it here:

Imagine a needle lands randomly on a drawing of two parallel horizontal lines. The lines are further apart than the length of the needle. What are the chances that the needle will land in such a way that it touches one of the lines?

This is one of those problems that seem impossible to solve the first time you hear it, but it is solvable. There's no need to spend any time calculating the solution here, though I certainly could do it, I assure you. Really, I could. Really. The solution has to do with geometry, and it takes into account two key components of information. The keys to any given random landing position are:

• Where the center of the needle is in terms of distance from the closest line

• The angle of the needle in relationship to the perpendicular of the closest line

Defining the random position of the needle with these two bits of information allows for some general observations that help to simplify the problem:

• If the center of the needle is exactly on one of the lines, then the needle will always touch that line, regardless of its angle.

• If the center of the needle is close enough to a line, within half the needle's length, then the needle will sometimes touch a line. The angle of the needle determines whether the needle touches a line.

• If the center of the needle is further away from a line than half the needle's length, then the needle will never touch that line, regardless of its angle.

• The closer to a line, the greater the chances are of a needle touching that line.

All the possible needle locations can be graphed as a curve, illustrating all possible distances from a line and all possible angle-from-perpendiculars of the needle. Trigonometry enters the picture here, and mathematicians have defined such a curve with this equation:

This is the answer to the problem. Let's try it quickly with some real numbers, just to check Leclerc's work. Imagine a needle three inches long falling randomly on a sewing table with a pattern on the grain such that there are two parallel lines four inches apart. What proportion of the time will the needle touch one of the two lines? Here are the necessary computations:

The needle will touch a line about 48 percent of the time.

Already, your gambling juices might be flowing as you envision a large room full of needle-dropping and lines on the floor and such. Go for it; more power to you. This principal is already in play in some carnival games you've probably seen. Ever notice how rarely those ping-pong balls land in those fishbowls or the football gets through that hoop?

Probability and Pi

I promised you that you could use chance to estimate pi, though, not use pi to figure chance. The power of math allows us to move around any element of any equation, and so any element to the right of the equals sign can be moved to the left. We can scramble our probability equation to produce a pi equation like so:

I'll prove it works by using the same numbers we used when we tested the probability equation. We already know what the right answer for pi is, so let's see if the equation works:

This equation calculates pi as 3.1447, which is pretty darn close to 3.14159. If we had allowed our numbers to go many places past the decimal, we would have had an even more accurate answer.

Estimating Pi Using Probability

In our example, we knew the probability, so we could calculate pi using that information. But what if you didn't know pi and needed to calculate it? What if you were stuck on a desert island or on a long ocean voyage or in bed with a broken leg and had no access to reference works that included a fairly exact value for pi? Further, suppose you needed to calculate the circumference of a circle or the volume of a sphere or any of a number of other values in geometry or finance or physics that make use of the pi value? A nightmare scenario, eh? You could use this formula to calculate pi pretty accurately by just conducting an experiment and collecting data.

Set up an area with two horizontal lines, drop some needles, and keep track. Measure the distance between your lines and the length of your needle, and let the random whims of chance do all the cognitive heavy lifting. Collect a large sample of data from many needle drops to get a probability that is precise to several places past the decimal, perhaps a thousand drops or so. Good luck and keep careful records.

Let's say that you drew two lines that were 8 inches apart and used a knitting needle about 7 inches long. If you used this equipment for a large number of drops, you would likely find that the needle touched a line somewhere between 50 and 60 percent of the time. Let's say it was 55 percent. To use this data to calculate pi, you would apply the math like this:

You'll find that 3.18 is pretty close to the ratio of the circumference to the diameter shown in Figure 5-6.

If your eyesight isn't what it used to be, there's no need to use a hard-to-see needle. You can apply the same logic using a pencil falling off your desk, or a marble rolling across the floor into a defined area, or a parachutist landing on a rectangular target. You need two parallel lines that the pencil, marble, or parachutist can have a chance of landing on, and you need to know the length of the object. As long as the outcome is random, anything will work, and a parachutist landing on a haystack is a lot easier to find than a needle somewhere in one.