Hack 45. Amaze Your 23 Closest Friends

What are the chances of at least two people in a group sharing a birthday? Depending on the number of people present, surprisingly high. Impress your friends at parties (and perhaps win some money in a bar bet) using these simple rules of probability.

Some events that seem logically unlikely can actually turn out to be quite probable in some cases. One such example is determining the probability that at least two people in a group share a birthday. Many people are shocked to learn that as long as there are at least 23 people in the group, there is a better than 50 percent chance that at least 2 of them will have the same birthday! By using a few simple rules of probability, you can figure out the likelihood of this event occurring for groups of any size, and then amaze your friends when your predictions come true.

You could also use this result to make some cash in a bar bet (as long as there are at least 23 people there).

So, how do you figure out the probability of at least two people sharing a birthday? To solve this problem, you need to make a couple of assumptions about how birthdays are distributed in the population and know a few rules about how probabilities work.

Getting Started

To determine the chances of at least two people sharing a birthday, we have to make a couple of reasonable assumptions about how birthdays are distributed. First, let's assume that birthdays are uniformly distributed in the population. This means that approximately the same number of people are born on every single day of the year.

This is not necessarily perfectly true, but it's close enough for us to still trust our results. However, there is one birthday for which this is definitely not true: February 29, which occurs only every four years on Leap Year. The good news is that few enough people are born on February 29 that it is easy for us to just ignore it and still get accurate estimates.

Once we've made these two assumptions, we can solve the birthday problem with relative ease.

Applying the Law of Total Probability

In our problem, there are only two mutually exclusive possible outcomes:

• At least two people share a birthday.

• No one shares a birthday.

Since one of these two things must occur, the sum of the two probabilities will always be equal to one. Statisticians call this the Law of Total Probability, and it comes in handy for this problem.

The term mutually exclusive means that if one event occurs, the other one cannot occur, and vice versa.

A simple coin-flipping example can help picture how this works. With a fair coin, the probability of getting a heads is 0.5, just as the probability of getting a tails is 0.5 (which is another example of mutually exclusive events, because the coin can't come up heads and tails in the same flip!). Once you flip the coin, one of two things has to happen. It must land either heads up or tails up, so the probability of heads or tails occurring is 1 (0.5 + 0.5). Conversely, we can think of the probability of heads as one minus the probability of tails (1 - 0.5 = 0.5), and vice versa.

Sometimes, it's easier to determine the probability of an event not occurring and then use that information to determine the probability that it will occur. The probability of no one sharing a birthday is a bit easier to figure out, and it depends only on how many people are in the group.

Imagine that our group contains only two people. What's the probability that they share a birthday? Well, the probability that they don't share a birthday is easy to figure: person #1 has some birthday, and there are 364 other birthdays person #2 might have that would result in them not sharing a birthday. So, mathematically, it's 364 divided by 365 (the total number of possible birthdays), or 0.997.

Since the probability of the two people not sharing a birthday is 0.997 (a very high probability), the probability of them actually sharing a birthday is equal to 1 - 0.997 (0.003, a very low probability). This means that only 3 out of every 1,000 randomly selected pairs of people will share a birthday. So far, this makes perfect logical sense. However, things change (and change quickly) once we start adding more people to our group!

Calculating the Probability of Independent Events

The other trick we need to solve our problem is applying the idea of independent events. Two (or more) events are said to be independent if the probability of their co-occurrence is equal to the product of their individual probabilities.

Once again, this is simple to understand with a nice, easy coin-flipping example. If you flip a coin twice, the probability of getting heads twice is equal to the probability of heads multiplied by the probability of heads (0.5x0.5 = 0.25), because the outcome of one coin flip has no influence on the outcome of the other (hence, they are independent events).

So, when you flip a coin twice, one out of every four times the results will be two heads in a row. If you wanted to know the probability of flipping three heads in a row, the answer is 0.125 (0.5x0.5x0.5), which means that three heads in a row happens only one time out of every eight.

In our birthday problem, every time we add another person to the group, we've added another independentevent (since one person's birthday doesn't influence anyone else's birthday), and thus we'll be able to figure out the probability of at least two of those people sharing a birthday, regardless of how many people we add; we'll just keep on multiplying probabilities together.

To review, no matter how many people are in our group, only one of two mutually exclusive events can occur: at least two people share a birthday or no one shares a birthday. Because of the Law of Total Probability, we know that we can determine the probability of no one sharing a birthday, and one minus that value will be equal to the probability that at least two share a birthday. Lastly, we also know that each person's birthday is independent of the other group members. Got all that? Good, let's proceed!

Solving the Birthday Problem

We've already determined that the probability of two people not sharing a birthday in a group of two is equal to 0.997. Let's say we add another person to the group. What is the probability of no one sharing a birthday? There are 363 other birthdays person #3 could have that would result in none of them sharing a birthday. The probability of person #3 not sharing a birthday with the other two is therefore 363/365, or 0.995 (slightly lower).

But remember, we're interested in the probability that no one shares a birthday, so we use the rule of independentevents and multiply the probability that the first two won't share a birthday by the probability that the third person won't share a birthday with the other two: 0.997x0.995 = 0.992. So, in a group of three people, the probability that none of them share a birthday is 0.992, which means that the probability that at least two of them share a birthday is 0.008 (1 - 0.992).

This means that only 8 out of every 1,000 randomly selected groups of 3 people will result in at least 2 of them sharing a birthday. This is still a pretty small chance, but note that the probability has more than doubled by moving from two people to three (0.003 compared to 0.008)!

Once we start adding more and more people to our group, the probability of at least two people sharing a birthday starts to increase very quickly. By the time our group of people is up to 10, the probability of at least 2 sharing a birthday is up to 0.117. How do we determine this in general? For every person added to the group, another fraction is multiplied by the previous product. Each additional fraction will have 365 as the denominator, and the numerator will be 365 minus the number of additional people beyond the first.

So, for our previously mentioned group of 10 people, the numerator for the last fraction is 356 (365 - 9), determined like so:

This tells us that the probability of no one sharing a birthday in a group of 10 people is equal to 0.883 (much lower than what we saw for 2 or 3 people), so the probability that at least 2 of them will share a birthday is 0.117 (1 - 0.883).

The first fraction is the probability that the second person won't share a birthday with the first person. The second fraction is the probability that the third person won't share a birthday with the first two. The third fraction is the probability that the fourth person won't share a birthday with the first three, and so on. The ninth and final fraction is the probability that the tenth person won't share a birthday with any of the other nine.

In order for no one to share a birthday, every single one of the events in the chain has to co-occur, so we determine the probability of all of them happening in the same group of people by multiplying all of the individual probabilities together. Every time we add another person, we include another fraction into the equation, which makes the final product get smaller and smaller.

Solving for Almost Any Group Size

As the group size increases, it becomes increasingly more likely that at least two people will share a birthday. This makes perfect sense, but what surprises most people is how quickly the probability increases as the group gets bigger. Figure 4-3 illustrates the rate at which the probability goes up when you add more and more people.

Figure 4-3. Chances of matching birthdays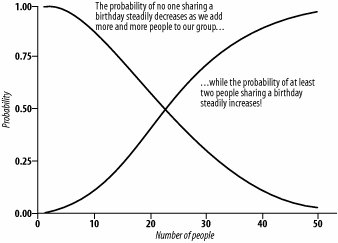

For 20 people, the probability is 0.411; for 30 people, it's 0.706 (meaning that 7 times out of 10 you will win money on your bet, which are pretty good odds). If you have 23 people in your group, the chances are just slightly better than 50/50 that at least 2 people will share a birthday (the probability is equal to 0.507).

When all is said and done, this is a pretty neat trick that never ceases to surprise people. But remember to make the bar bet only if you have at least 23 people in the room (and you're willing to accept 50/50 odds). It works even better with more people, because your chances of winning go up dramatically every time another person is added. To have a better than 90 percent chance of winning your bet, you'll need 41 people in the room (probability of at least 2 people sharing a birthday = 0.903). With 50 people, there's a 97 percent chance you'll win your money. Once you have 60 people or more, you are practically guaranteed to have at least 2 people in the room who share a birthday and, of course, if you have 366 people present, there is a 100 percent chance of at least 2 people sharing a birthday. Those are great odds if you can get someone to take the bet!

William Skorupski