7.3 Estimating parameters and distributions
|
| < Free Open Study > |
|
7.3 Estimating parameters and distributions
Now that we have discussed various aspects of queuing theory, we should review some of the ways that we can parameterize the models that we choose. In this section, we will discuss various methods that can be used to determine whether a certain statistic or distribution appropriately describes an observed process. Specifically, we will cover hypothesis testing, estimators for some statistics, and goodness of fit tests. We will start with hypothesis testing in general.
A hypothesis test is a technique used to determine whether or not to believe a certain statement about a real-world phenomenon and to give some measure as to what degree to believe the statement. A hypothesis is usually stated in two parts: the first concerning the statistic or characteristic that we are hypothesizing about and the second concerning the value that is postulated for the statistic. For example, we may hypothesize that the mean value of an observed process is less than 10 or that the observed process is Gaussian. The positive statement of a hypothesis is usually called the null hypothesis and is denoted as H0. Associated with the null hypothesis is an alternative, denoted H1. The idea here is to have the two hypotheses complement each other so that only one will be selected as probable. The two hypotheses, H0 and H1, form the basis for the hypothesis test methodology outlined in the following paragraph.
A hypothesis test is usually performed in four general steps, which lead to the acceptance or rejection of the initial hypothesis. The first step is to formulate the null hypothesis H0 and the alternative hypothesis H1. Next, decide upon a statistic to test against. The statistic is typically the sample mean or variance. Third, a set of outcomes for the test statistic is chosen so that the outcome of the test statistic will fall within the set with a specific probability, given that H0 is true. That is, if H0 is true, we say that the value of the test statistic will fall within the set selected (sometimes called the critical region) with probability P (also called the test's level of significance). The idea is to select a critical region so that the probability of the test statistic value falling within the region is small, typically between 0.01 and 0.05. An occurrence of this event, then, indicates that the hypothesis H0 is not a good choice and should be rejected. Conversely, we could select a large probability, say 0.9, in which case the occurrence of the event indicates that the null hypothesis should be accepted. The final step in the process is to collect some sample data and to calculate the test statistic.
The next immediate problem for performing a hypothesis test is to define the expressions that describe the sample statistics we are interested in. These are commonly referred to as estimators, because they estimate the statistic that could be derived from a distribution that exactly models the real process. The most commonly used estimators are the sample mean and the sample variance.
In order to calculate the sample statistics, we must first obtain a random sample from the experimental population. A random sample is defined here as a sequence of observations of the real-world process, where each value observed has an equal probability of being selected and where each observation is independent of the others in the sample. Thus, a random sample is a sequence of random variables that are independent and identically distributed.
For a random sample of size n, where n is the number of samples obtained, the sample mean is defined as:
| (7.85) |
The sample variance is defined as:
| (7.86) |  |
The sample standard deviation is defined as it was for the standard deviation of a distribution and is repeated here as:
| (7.87) |
In the above three expressions, the random variable Xi represents the ith observation in the random sample.
Now that we can calculate the statistics for a random sample of some phenomenon, how can we relate these estimates to the actual statistics of the underlying process? For this, we use a theorem known as the sampling theorem. It states that, for a random sample, as previously described, with a finite mean, the sample mean and expected value are equivalent and the sample variance and the variance are also equivalent. That is, the sample statistics are said to be consistent, unbiased estimators. The sampling theorem also states several other important relations, including the following expression relating the variance of the sample mean and the variance of the random variable describing the process. This expression:
| (7.88) |
states that as the sample size gets larger, the variance of the sample mean gets smaller, indicating that it is closer to the true mean of X.
These estimates lead to still another question: Given that we know (or think that we know) the type of distribution that our random sample comes from, how do we estimate the parameters of such a distribution from the random sample data? There are two widely used methods for doing just this: the method of moments and the method of maximum likelihood estimation.
The method of moments is useful when we think we know the distribution of the sample but do not know what the distribution parameters are. Suppose the distribution whose parameters we wish to estimate has n parameters. In this method, we first find the first n distribution moments, as described in Chapter 5. Next, we calculate the first n sample moments and equate the results to the moments found earlier. From this we get n equations in n unknowns, which can then be solved simultaneously for the desired parameters. We derive the kth sample moment for a sample size of m samples as:
| (7.89) |  |
where Xi is the i sample point in the random sample.
In maximum likelihood estimation, we try to pick the distribution parameters that maximize the probability of yielding the observed values in the random sample. To do this, we first form what is called the likelihood function. This consists of the values of the assumed probability distribution function at the points observed in the random sample. This function, for a continuous random variable whose distribution has only one parameter, is:
| (7.90) |
For a random variable whose distribution has n parameters, we will have n equations, similar to equation (7.90). We then find the maximum of each equation with respect to each parameter. Finally, the set of n equations in n unknowns can be solved for the necessary parameters.
Now that we have outlined several methods for estimating the statistics of a distribution that describes the real-world process, we turn our attention to the reliability of our estimates. One measure of this reliability is called the confidence interval. A confidence interval is defined as a range of values, centered at the estimate of the statistic of interest, where the actual value of the statistic will fall within a fixed probability. For example, a 90-percent confidence interval for the mean of a particular random variable based upon a given sample may be defined as the range of values within a distance, r, of the estimated mean. In this case, r is chosen so that the fraction of times that an actual mean lands within the interval is 90 percent. The general procedure for defining a confidence interval requires the construction of a known distribution, say C, from the estimates of the statistic being estimated. Next, we pick an interval so that:
| (7.91) |
where z is the desired confidence level. Finally, we evaluate C using the value Xi so that the relationship:
| (7.92) |
is maintained. We can alternatively solve C for the points Xa and Xb, where C(Xa) = a and C(Xb) = b. These are the end points of the 100-percent confidence interval.
This procedure assumes that we know the distribution of C before we find the confidence interval. If this is not the case, and the sample size is large, we can assume that the sample distribution is normal and can obtain a reliable confidence interval for the value of the mean. In this case, we first form the statistic:
| (7.93) |
Since X is assumed normal, T in this case is also normal with a mean of 0 and a standard deviation of 1. Again, we define a percent confidence interval and determine a and b so that:
| (7.94) |
The desired confidence interval for the mean is then given by:
| (7.95) |
Confidence intervals for the variance when the population distribution is unknown can be found using the previously described method, although the results will be poor if the actual population distribution is far from normal.
Now that we have explored several techniques for estimating the parameters of distributions, we will look at some methods for finding a distribution that fits the sampled data. Typically, we will have found the sample mean and standard deviation and now want to find a random variable that adequately represents the sample population. The tests employed here are usually called goodness of fit tests. We will discuss two tests, the chi-square test and the Kolmogorov-Smirnov test. These tests fall under the general heading of hypothesis testing, and, therefore, we use the same hypothesis-forming techniques described earlier. In both tests, we start with a null hypothesis that the population has a certain distribution, and then we obtain a statistic that indicates whether we should accept the null hypothesis.
In the chi-square test, we determine whether the distribution of the null hypothesis appropriately fits the population by comparing the categories of the collected sample value to what can be generated by the assumed distribution. The premise is that we can find k bins, B1, ..., Bk, so that each value in the random sample falls into one, and only one, bin. After finding an appropriate set of bins, we partition the samples into them and record the number of samples that land in each. Next, we take a corresponding number of samples from the hypothesized population distribution and allocate them to the same bins. If any of the second set of samples (those taken from the distribution) fail to fall in only one bin, we have not selected an appropriate set of bins and must choose another set. For whatever type of distribution that we are testing against, the appropriate distribution parameters can be found using one of the estimation techniques described earlier. Continuing with the test, we now calculate the following statistic:
| (7.96) |  |
where NSi denotes the number of elements in bin i due to the random sample, and NDi is the number in bin i due to the hypothesized distribution. The basis of this test is that the statistic of equation (7.96) has a chi-square distribution. The degree of freedom of the chi-square distribution is defined as one less than the number of sample bins minus the number of parameters in the hypothesized distribution:
| (7.97) |
Next, we decide on the level of significance that we wish to test for. Using the following expression, we can calculate the probability density function for a chi-square distribution with n degrees of freedom:
| (7.98) | 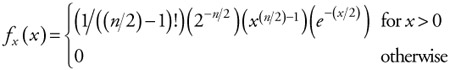 |
The final step is to find the value of X for which the integral with respect to x of equation (7.98), evaluated from x to infinity, is equal to the desired level of significance. The final test states that if the value of x just found is greater or equal to the chi-square statistic calculated in equation (7.96), the assumed distribution is not a good fit at the desired level of significance. That is, we reject the null hypothesis if:
| (7.99) |
An alternative approach for the chi-square test is to form the value C- ε, where ε is some small value. We then use the result to find the probability that x is greater than C- ε. The resultant probability gives us an indication as to the approximate level or significance that we may accept the null hypothesis. Several references give tables for the critical values of the chi-square distribution. These tables may be used in place of calculating the distribution values.
Another so-called goodness of fit test is the Kolmogorov-Smirnov test. The test is based upon the magnitude ordering of the sample, the calculation of the maximum difference between the sample points and the assumed distribution, and a determination of the level of fit of the assumed distribution. A formal description of this test appears in a number of statistics texts. Here we will describe a more intuitive approach, which is somewhat easier to experiment with.
As mentioned earlier, the first step of this test is to arrange the sample values in ascending order according to magnitude. For each point xi in the arranged sample, we find the fraction, fi, of the number of total samples that is less in magnitude than the given value. Next, for the assumed distribution, we find the value, Ki, that will yield the same fraction, fi, for a given number of samples. Finally, we plot Ki versus xi for all i. The resulting plot will indicate a good fit if the data form approximately a straight line with a slope of unity. If the fit is a straight line with a slope other than unity, the assumed distribution parameters may be tuned to achieve the desired results. Otherwise, we should try another assumed distribution.
|
| < Free Open Study > |
|
EAN: 2147483647
Pages: 136