9.4 Belief Revision and Conditional Logic

It is perhaps not surprising that there should be a connection between belief revision and the conditional logic considered in Section 8.6, given that both use plausibility measures as a basis for their semantics. Indeed, one approach to belief revision, called the Ramsey test (named after Frank Ramsey, who first proposed it; this is the same Ramsey who provided the first justification of the subjectivist view of probability, as mentioned in the notes to Chapter 2), basically defines belief revision in terms of conditional logic. The idea is that an agent should believe ψ after observing or learning φ iff he currently believes that ψ would be true if φ were true (i.e., if he currently believes φ → ψ). As the following theorem shows, this connection holds in reliable BCSs that satisfy REV1 and REV3:

Theorem 9.4.1

Suppose that 퓙 is a reliable BCS that satisfies REV1 and REV3. If r is a run in 퓙 such that o_{(r, m+1)} = φ, then (퓙, r, m) ⊨ φ → ψ iff (퓙, r, m + 1) ⊨ B ψ. Equivalently, if s_a φ is a local state in 퓙, then

Proof See Exercise 9.15.

A priori, it could be the case that Theorem 9.4.1 is an artifact of the semantics of BCSs. The next result, Theorem 9.4.2, shows that there is an even deeper connection between the AGM postulates and conditional logic, which goes beyond the use of BCSs to model belief revision. Roughly speaking, the theorem shows that a system satisfies the AGM postulates iff it satisfies all the properties of P as well as Rational Monotonicity. Theorem 9.4.2 can be viewed as strengthening and making precise the remarks that I made earlier about R6 being essentially LLE and R8 being Rational Monotonicity in disguise.

Theorem 9.4.2

Suppose that ⊢ (as used in R5) corresponds to provability in propositional logic.

Suppose that ∘ satisfies R1–8. Fix a belief set K, and define a relation → on formulas by taking φ → ψ to hold iff ψ ∊ 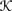∘ ψ . Then → satisfies all the properties of P as well as Rational Monotonicity: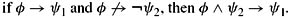

Moreover, φ → false iff φ is not satisfiable.
Conversely, suppose that → is a relation on formulas that satisfies the properties of P and Rational Monotonicity, and φ → false iff φ is not satisfiable. Let K ={ψ : true → ψ}. Then K is a belief set. Moreover, if ∘ is defined by taking K ∘ φ ={ψ : φ → ψ}, then R1–8 hold for K and ∘.

Proof For part (a), suppose that ∘ satisfies R1–8. Fix K and define φ → ψ as in the statement of the theorem. The fact that → satisfies REF follows immediately from R2. RW and AND both follow from the fact that K ∘ φ is a belief set (i.e., R1). LLE is immediate from R6. The fact that φ → false iff φ is not satisfiable is immediate from R5. It remains to prove OR, CM, and Rational Monotonicity.

For the OR rule, suppose that φ₁ → ψ and φ₂ → ψ. Thus, ψ ∈ K ∘ φ₁ ∩ K ∘ φ₂. By R2, φ₁ ∨ φ₂ ∈ K ∘ (φ₁ ∨ φ₂). Thus, it cannot be the case that both φ₁ ∈ K ∘ (φ₁ ∨ φ₂) and φ₂ ∈ K ∘ (φ₁ ∨ φ₂). Without loss of generality, suppose that φ₁ ∉ K ∘ (φ₁ ∨ φ₂). By R6, R7, and R8, it follows that

Since ψ ∈ K ∘ φ₁, it follows that ψ ∈ Cl(K ∘ (φ₁ ∨ φ₂) ∪{φ₁}), and so

There are now two subcases to consider. First suppose that φ₂ ∉ K ∘ (φ₁ ∨ φ₂). Then the same arguments used to prove (9.8) also show that K ∘ (φ₁ ∨ φ₂) ⊢ φ₂ ↠ ψ. It follows that K ∘ (φ₁ ∨ φ₂) ⊢ (φ₁ ∨ φ₂) ↠ ψ. Since K ∘ (φ₁ ∨ φ₂) is a belief set (and thus is closed), it follows that (φ₁ ∨ φ₂) ↠ ψ ∈ K ∘ (φ₁ ∨ φ₂). By R2, (φ₁ ∨ φ₂) ∈ K ∘ (φ₁ ∨ φ₂). Hence, ψ ∈ K ∘ (φ₁ ∨ φ₂). On the other hand, if φ₂ ∈ K ∘ (φ₁ ∨ φ₂), then since φ₁ ∨ φ₂ ∈ K ∘ (φ₁ ∨ φ₂), it follows that φ₁ ∈ K ∘ (φ₁ ∨ φ₂). It now again easily follows using (9.8) that ψ ∈ K ∘ (φ₁ ∨ φ₂). In either case, by definition, φ₁ ∨ φ₂ → ψ, so the OR rule holds.

For Rational Monotonicity, note that if φ ↛ ψ₂, by R7 and R8, K ∘ (φ ∧ ψ₂) = Cl(K ∘ φ ∪{ψ₂}). If, in addition, φ → ψ₁, then ψ₁ ∈ K ∘ φ, so ψ₁ ∈ Cl(K ∘ φ ∪{ψ₂}) = K ∘ (φ ∧ ψ₂). Thus, φ ∧ ψ₂ → ψ₁. The argument for CM is similar.

For part (b), suppose that → satisfies the properties of P and Rational Monotonicity, and K and ∘ are defined as in the theorem. It follows from AND and RW that K is a belief set. Moreover, for any fixed φ, the same argument shows that K ∘ φ is a belief set, so R1 holds. By REF, R2 holds. R5 holds since φ → false iff φ is not satisfiable. It remains to prove R3, R4, R7, and R8. I leave the proof of R7 and R8 to the reader (Exercise 9.16). The proof of R3 and R4 is similar (and simpler).