6.2 Probability Frames

6.2 Probability Frames

The analogue of an epistemic frame in the case where uncertainty is represented using probability is a probability frame. It has the form (W, ₁, …, _n), where, as before, W is a set of worlds, and _i is a probability assignment, a function that associates with each world w a probability space (W_w,i, _w,i, μ_w,i). Although it is possible to take W_{w, i} = W (by extending μ_w,i so that it is 0 on all sets in W − W_{w, i}), it is often more convenient to think of μ_{w, i} as being defined on only a subset of W, as the examples in this chapter show. The special case where n = 1 and ₁(w) = (W, , μ) for all w ∈ W can be identified with a standard probability space; this is called a simple probability frame.

Example 6.2.1

Consider the frame F described in Figure 6.2.

There are four worlds in this frame, w₁, …, w₄. ₁ and ₂ are defined as follows:

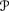
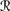• ₁(w₁) = 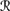₁(w₂) = ({w₁, w₂} μ₁), where μ₁ gives each world probability 1/2;

• ₁(w₃) = 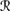₁(w₄) = ({w₃, w₄} μ₂), where μ₂ gives each world probability 1/2;

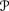
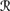• ₂(w₁) = 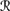₁(w₃) = ({w₁, w₃} μ₃), where μ₃(w₁) = 1/3 and μ₃(w₃) = 2/3;

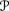
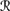• ₂(w₂) = ₁(w₄) = ({w₂, w₄} μ₄), where μ₄(w₂) = 2/3 and μ₄(w₄) = 1/3.

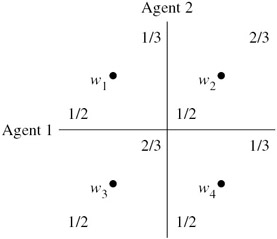
Figure 6.2: A probability frame.

In epistemic frames, conditions are typically placed on the accessibility relations. Analogously, in probability frames, it is often reasonable to consider probability assignments that satisfy certain natural constraints. One such constraint is called uniformity:

Recall that the Euclidean and transitive property together imply that if v ∈ _i(w), then _i(w) = _i(v); uniformity is the analogue of these properties in the context of probability frames.

Other natural constraints can be imposed if both knowledge and probability are represented. An epistemic probability frame has the form M = (W, ₁, …, _n, ₁, …, _n). Now it is possible to consider constraints on the relationship between _i and _i. The standard assumption, particularly in the economics literature (which typically assumes that the _is are equivalence relations) are that (1) an agent's probability assignment is the same at all worlds that she considers possible and (2) the agent assigns probability only to worlds that she considers possible. The first assumption is called SDP (state-determined probability). It is formalized as follows:

The reason for this name will become clearer later in this chapter, after I have presented a framework in which it makes sense to talk about an agent's state. SDP then says exactly that the agent's state determines her probability assignment. The second assumption can be viewed as a consistency assumption, so it is abbreviated as CONS.

In the presence of CONS (which I will always assume), SDP clearly implies UNIF, but the converse is not necessarily true. Examples later in this chapter show that there are times when UNIF is a more reasonable assumption than SDP.

One last assumption, which is particularly prevalent in the economics literature, is the common prior (CP) assumption. This assumption asserts that the agents have a common prior probability on the set of all worlds and each agent's probability assignment at world w is induced from this common prior by conditioning on his set of possible worlds. Thus, CP implies SDP and CONS (and hence UNIF), since it requires that _i(w) = W_w,i. There is one subtlety involved in making CP precise, which is to specify what happens if the agent's set of possible worlds has probability 0. One way to deal with this is just to insist that this does not happen. An alternative way (which is actually more common in the literature) is to make no requirements if the agent's set of possible worlds has probability 0; that is what I do here. However, I do make one technical requirement. Say that a world w′ is reachable from w if there exist worlds w₀,…, w_m with w₀ = w and w_m = w′ and agents i¹,…, i_m such that w_j ∈ _ij (w_j−1) for j = 1,…, m. Intuitively, w′ is reachable from w if, in world w, some agent considers it possible that some agent considers it possible that … w′ is the case. Let C(w) denote the worlds reachable from w. I require that C(w) have positive prior probability for all worlds w ∈ W. The reason for this technical requirement will become clearer in Section 7.6.

CP. There exists a probability space (W, _W, μ_W) such that _i(w), C(w) ∈ _W, μ_W(C(w)) > 0, and _i(w = (_i(w), _W|_i(w), μ_w,i) for all agents i and worlds w ∈ W, where _W|_i(w) consists of all sets of the form U ∩ _i(w) for U ∈ _W, and μ_w,i = μ_W|_i(w) if μ_W(_i(w)) > 0. (There are no constraints on μ_w,i if μ_W(_i(w)) = 0.)

Until quite recently, the common prior assumption was almost an article of faith among economists. It says that differences in beliefs among agents can be completely explained by differences in information. Essentially, the picture is that agents start out with identical prior beliefs (the common prior) and then condition on the information that they later receive. If their later beliefs differ, it must thus be due to the fact that they have received different information.

CP is a nontrivial requirement. For example, consider an epistemic probability frame F = ({w₁, w₂}, ₁, ₂, ₁, ₂) where both agents consider both worlds possible, that is, ₁(w₁) = ₁(w₂) = ₂(w₁ = ₂(w₂) = {w₁, w₂}. It is easy to see that the only way that this frame can be consistent with CP is if ₁(w₁) = ₂(w₁) = ₁(w₂) = ₂(w₂)(Exercise 6.3). But there are less trivial constraints placed by CP, as the following example shows:

Example 6.2.2

Extend the probability frame F from Example 6.2.1 to an epistemic probability frame by taking (w₁) = (w₂) = {w₁, w₂}, (w₃) = ₁(w₄) = {w₃, w₄}, ₂(w₁) = ₁(w₃) = {w₁, w₃}, and ₂(w₂) = ₁(w₄) = {w₂, w₄}. It is not hard to show that this frame does not satisfy CP (Exercise 6.4).

The assumptions CONS, SDP, UNIF, and CP can be characterized axiomatically. I defer this discussion to Section 7.6.