A.3 Summation

A.3 Summation

Summation of a series of numbers is frequently used in statistical and communication theory. A shorthand notation is used to represent a series of additions:

• Σ (Sigma), used to denote "the sum of."

where the general form is:

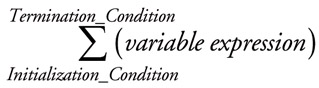
For example:

represents the sum of the series X₁ + X₂ + X₃ + ... X_n. To illustrate, if n = 4 and the series of numbers is {1, 2, 3, 4}, then this operation would produce the result 10. Note that the variable expression must be summed before any external operator can be applied; so for example:

This is clearly demonstrated using the previous example series {1, 2, 3, 4} and n = 4.

• 1² + 2² + 3² + 4² ≠ (1 + 2 + 3 + 4)²

• 30 ≠ 100

Summation is frequently used with more complex variable expressions, such as summation of a series of products:

It is important to recognize here that the first instance of x is multiplied by the first instance of y and so on through the series. There are a number of other basic rules applicable to summation operations, these include:

• Rule 1: The summation of the sum of two variables is equal to the sum of the two summations of those variables:

  

• Rule 2: The summation of the subtraction of two variables is equal to the difference between the two summations of those variables:

  

• Rule 3: The summation of a constant n times is equal to the product of n and that constant:

  

• Rule 4: The summation of the product of a constant and a variable is equal to the product of the constant and the summation of that variable: