Isometric 3D

Overview

After so much work with perspective in the scaling chapter, it may seem odd that in this chapter we're going to abandon perspective entirely. That's right, we're going to explore 3D without perspective. If you've grown up in a Western country, you may be thinking that the previous sentence is an oxymoron. Isn't 3D all about perspective? Well, not really.

As we mentioned in the earlier chapter on scaling, what we commonly call perspective (more precisely, linear perspective ) is not a natural phenomenon ”it was developed as part of the Renaissance movement in Europe. Linear perspective, based on a model relying on the existence of vanishing points where all lines in a scene converge and a single point of gaze for the user , was embraced, further developed, and grew ubiquitous in the West. In the East, however, the Chinese were using a very different method of pictorial representation. Their pictures were not snapshots in time like Western pictures were; instead, they were stories. Drawn on huge scrolls , "reading" them would be a journey in time through a narrative.

Jan krikke, in his excellent online essay "A Chinese Perspective for Cyberspace?" gives a wonderful example of such a scroll depicting life along a river: "Upon unrolling the opening sequence of the scroll, we may see people boarding a boat on a river. As we unroll the scroll further, we see the boat cross a lake, navigate rapids in the river , stop at a small harbour, and lastly arrive at its destination on the seashore. In other words, the scroll has taken the viewer through an experience in space and time." ( http://iias.leidenuniv.nl/iiasn/iiasn9/eastasia/krikke.html )

Instead of using vanishing points and relying on optical principles that would break the continuity of the story, the Chinese kept all lines along their "z-axis" parallel. In doing this, they developed axonometric projection. The term axonometric is the marriage of the Greek word axon , meaning axis, and the English word metric, meaning measure. Literally, it means measure from the axis, since you can calculate the true length of lines in an axonometric image by measuring them and applying the necessary transformations (something you cannot do with linear perspective).

Thiadmer Riemersma has written the definitive introduction to axonometric projections. You can read his whole paper at www.compuphase.com/axometr.htm .

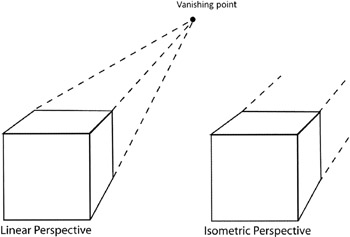
Isometric projection is one specific application of axonometric projection. If you break down the word isometric, you get iso , which means equal, and metric. This comes from the fact that if you were to draw a cube in an isometric universe, all of its sides would be the same length. Compare this to a cube drawn in linear perspective in the diagram below. Note how, as you travel from the front face to the back face of the cube with linear perspective, the diagonal lines converge and are foreshortened. However, as you can see below, all lines along the z-axis in an isometric projection are parallel. There is no foreshortening of diagonal lines and, if you know the angle of the projection used, you can calculate the actual length of a line by measuring it off the image and applying the correct calculation to it:

As mentioned earlier, isometric 3D refers to an axonometric projection where unit distances on the x-, y-, and z-axes are equal. There can also be different types of isometric projections, depending on the angle made between the z- and x-axes of the isometric world and the x-axis of the 2D Cartesian plane. The latter corresponds to the stage coordinates of Flash.

Camillo Trevisan has an amazing freeware program called Cartesio that you can download from www.iuav.it/dpa/ricerche/trevisan/intern02.htm to see the difference between many types of axonometric, isometric, and other types of projections.

The most common type of isometric projection uses a 30 angle. This angle of projection, first publicized by William Farish in 1822, is used extensively for architectural and technical drawings due to the fact that it is very easy to do calculations on it (since sin 30 = 0.5). However, another common version of isometric projection, especially with isometric computer games based on bitmap tiles, uses an angle of 25.56505 (approximately), or arctangent 0.5. This seemingly weird angle is used because it results in more aesthetically pleasing and proportional diagonal lines on a computer screen. This is a much bigger issue when graphics are not antialiased. In Flash, since both vectors and bitmaps can have antialiasing applied (where the edges are softened to remove jagged lines), you will see the 30 projection applied in isometric Flash games.

We're going to kick off this chapter with a look at the simplest type of parallel projection you can create in Flash: the 45 projection. It's especially easy to draw using this angle because Flash's Line Tool, when constrained using the SHIFT key, automatically snaps to 45 increments . Although this is an example of isometric projection, it is not what is commonly thought of when the term isometric is used in computer applications and games.