A.4 Lemma

---

A.4 Lemma

If g is stuck then .

Proof:	By induction on the structure of g.
Case:	g = true, false, or 0

Can't happen (we assumed that g is stuck).

Case:

g = if g₁ then g₂ else g₃

Since g is stuck, g₁ must be in normal form (or else E-IF would apply). Clearly, g₁ cannot be true or false (otherwise one of E-IFTRUE or E-IFFALSE would apply and g would not be stuck). Consider the remaining cases:

•  

  Subcase:

  g₁ = if g₁₁ then g₁₂ else g₁₃

• Since g₁ is in normal form and obviously not a value, it is stuck. The induction hypothesis tells us that 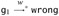. From this, we can construct a derivation of 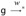if wrong then g₂ else g₃. Adding a final instance of rule E-IF-WRONG yields 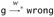, as required.

•  

  Subcase:

  g₁ = succ g₁₁

• If g₁₁ is a numeric value, then g₁ is a badbool and rule E-IF-WRONG immediately yields 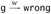. Otherwise, by definition g₁ is stuck, and the induction hypothesis tells us that 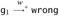. From this derivation, we construct a derivation of 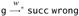. Adding a final instance of rule E-SUCC-WRONG yields .

• Other subcases:

• Similar.

Case:

g = succ g₁

Since g is stuck, we know (from the definition of values) that g₁ must be in normal form and not a numeric value. There are two possibilities: either g₁ is true or false, or else g₁ itself is not a value, hence stuck. In the first case, rule E-SUCC-WRONG immediately yields ; in the second case, the induction hypothesis gives us and we proceed as before.

Other cases:

Similar.

Lemmas A.3 and A.4 together give us the "only if" (Þ) half of Proposition A.2. For the other half, we need to show that a term that is "about to go wrong" in the augmented semantics is stuck in the original semantics.

---