35.

[Cover] [Contents] [Index]

Page 129

3.4.4 Issues relating to Hopfield networks

In order to use a Hopfield network for problem solving, one has to determine the number of processing units in the network, and define the energy function and weight matrix. The adequacy of the solution depends upon these choices. The energy function represents the problem to be solved. Careful construction of the energy function can reduce network search time, and help the network converge to an acceptable solution. Definition of a complete energy function generally involves the specification of two elements, called the objective function and the constraint function. The objective function gives a general measure of cost, such as the similarity between the features or the distance of travel. The constraint function describes limitations to the solution of the problem. For instance, in the travelling salesman problem, the objective function will be a measure of distance travelled by the salesman, while the constraint function addresses restrictions, such as the fact that each city may be visited only once, or that only one city can be visited per time period. More specifically, the constraint function acts as a penalty term that associates a high energy or cost with violations of the constraints. An example is presented in Section 3.4.5.

Two steps are required to determine the values of the elements of the weight matrix W. The first step is to define an energy function. The second step uses the specified energy function to obtain the weights w_ij in terms of Equation (3.32), which can be reduced to:

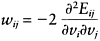(3.37)

The relationship between w_ij and energy E_ij is fully specified. Aiyer et al. (1990) give a theoretical analysis of the effect of the weight matrix W on the performance of Hopfield networks.

As in all optimisation problems, one has to consider the question of local and global minima. Since the energy function may contain many local minima, the network usually converges to a local minimum, as illustrated in Figure 3.13. Here, point c is the global minimum of the energy function, while points a and b are local minima. Thus, if the initial network state is located at point d, the network is very likely to converge at point a or b, but not c. If this situation arises then the optimisation procedure is said to have become trapped in a local minimum. To overcome this problem, a modified Hopfield network can be used, as described by Lee and Sheu (1991).

Another approach for attaining a global minimum is based on the technique of annealing, which can be explained by introducing a ‘temperature’ parameter to the system. The system convergence process will start at a

[Cover] [Contents] [Index]