A Pure Strategy
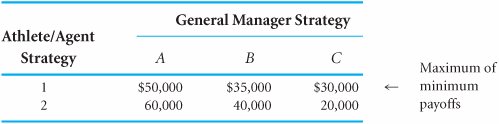
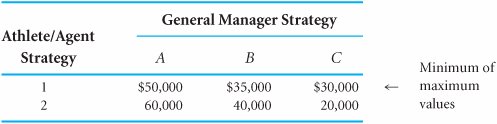
| When each player in a game adopts a single strategy as an optimal strategy, the game is a pure strategy game. The value of a pure strategy game is the same for both the offensive player and the defensive player. In contrast, in a mixed strategy game, the players adopt a mixture of strategies if the game is played many times. In a pure strategy game, each player adopts a single strategy as an optimal strategy . A pure strategy game can be solved according to the minimax decision criterion . According to this principle, each player plays the game to minimize the maximum possible losses. The offensive player selects the strategy with the largest of the minimum payoffs (called the maximin strategy), and the defensive player selects the strategy with the smallest of the maximum payoffs (called the minimax strategy). In our example involving the athlete's contract negotiation process, the athlete will select the maximin strategy from strategies 1 and 2, and the general manager will select the minimax strategy from strategies A, B, and C. We will first discuss the athlete's decision, although in game theory the decisions are actually made simultaneously . With the minimax decision criterion , each player seeks to minimize maximum possible losses; the offensive player selects the strategy with the largest of the minimum payoffs, and the defensive player selects the strategy with the smallest of the maximum payoffs . To determine the maximin strategy, the athlete first selects the minimum payoff for strategies 1 and 2, as shown in Table E.2. The maximum of these minimum values indicates the optimal strategy and the value of the game for the athlete. Table E.2. Payoff Table with Maximin Strategy The value $30,000 is the maximum of the minimum values for each of the athlete's strategies. Thus, the optimal strategy for the athlete is strategy 1. The logic behind this decision is as follows . If the athlete selected strategy 1, the general manager could be expected to select strategy C, which would minimize the possible loss (i.e., a $30,000 contract is better for the manager than a $50,000 or $35,000 contract). Alternatively, if the athlete selected strategy 2, the general manager could be expected to select strategy C for the same reason (i.e., a $20,000 contract is better for the manager than a $60,000 or $40,000 contract). Now, because the athlete has anticipated how the general manager will respond to each strategy, he realizes that he can negotiate either a $30,000 or a $20,000 contract. The athlete selects strategy 1 in order to get the larger possible contract of $30,000, given the actions of the general manager. Simultaneously, the general manager applies the minimax decision criterion to strategies A, B, and C. First, the general manager selects the maximum payoff for each strategy, as shown in Table E.3. The minimum of these maximum values determines the optimal strategy and the value of the game for the general manager. Table E.3. Payoff Table with Minimax Strategy The value $30,000 is the minimum of the maximum values for each of the strategies of the general manager. Thus, the optimal strategy for the general manager is C. The logic of this decision is similar to that of the athlete's decision. If the general manager selected strategy A, the athlete could be expected to select strategy 2 with a payoff of $60,000 (i.e., the athlete will choose the better of the $50,000 and $60,000 contracts). If the general manager selected strategy B, then the athlete could be expected to select strategy 2 for a payoff of $40,000. Finally, if the general manager selected strategy C, the athlete could be expected to select strategy 1 for a payoff of $30,000. Because the general manager has anticipated how the athlete will respond to each strategy, he realizes that either a $60,000, $40,000, or $30,000 contract could possibly be awarded. Thus, the general manager selects strategy C, which will result in the minimum contract of $30,000. In general, the manager considers the worst outcome that could result if a particular strategy were followed. Under the minimax criterion, the general manager will select the strategy that ensures that he loses only the minimum of the maximum amounts that could be lost. Solution of Game Theory Problems with QM for WindowsQM for Windows, which we use in the text to solve decision analysis problems, also has a module for solving game theory problems. The QM for Windows solution for our athlete/agent example is shown in Exhibit E.1. Notice that QM for Windows indicates the row minimums and column maximums, and it provides the maximin solution in the upper-right-hand corner of the solution table. Exhibit E.1.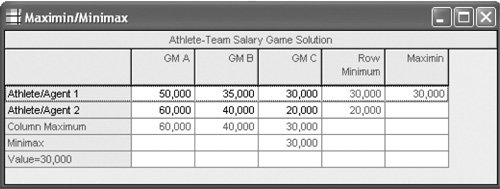 Dominant StrategiesWe could have reduced the choices of the general manager if we had noticed that strategy C dominates strategies A and B. Dominance occurs when all the payoffs for one strategy are better than the corresponding payoffs for another strategy. In Table E.3 the values $30,000 and $20,000 are both lower than the corresponding payoffs of $50,000 and $60,000 for strategy A and the corresponding payoffs of $35,000 and $40,000 for strategy B. Because strategy C dominates A and B, these two latter strategies can be eliminated from consideration altogether, as shown in Table E.4. If this had been done earlier, strategy C could have been selected automatically, without applying the minimax criterion. Thus, the most efficient approach is to first examine the payoff table for dominance in order to possibly reduce its size . A strategy is dominated, and can be eliminated, if all its payoffs are worse than the corresponding payoffs for another strategy . Table E.4. Payoff Table with Dominated Strategies Eliminated
The fact that the optimal strategy for each player in this game resulted in the same pay-off game value of $30,000 is what classifies it as a pure strategy game. In other words, because strategy 1 is optimal for the athlete and strategy C is optimal for the general manager, a contract for $30,000 will be awarded to the athlete. Because the outcome of $30,000 results from a pure strategy, it is referred to as an equilibrium point (or sometimes as a saddle point ). A point of equilibrium is a value that is simultaneously the minimum of a row and the maximum of a column , as is the payoff of $30,000 in Table E.3. In a pure strategy game, the optimal strategy for each player results in the same payoff, called an equilibrium , or saddle, point . It is important to realize that the minimax criterion results in the optimal strategy for each player as long as each player uses this criterion. If one of the players does not use this criterion, the solution of the game will not be optimal. If we assume that both players are logical and rational, however, we can assume that this criterion will be employed. The equilibrium point in a game is simultaneously the minimum of a row and the maximum of a column . If an equilibrium point exists, it makes the determination of optimal strategies relatively easy because no complex mathematical calculations are necessary. However, as mentioned earlier, if a game does not involve a pure strategy, it is a mixed strategy game. We will discuss mixed strategy games next . The minimax criterion will result in the optimal strategies only if both players use it . |
EAN: 2147483647
Pages: 358