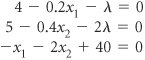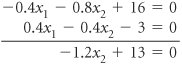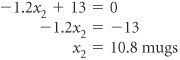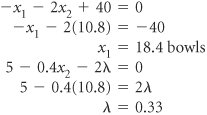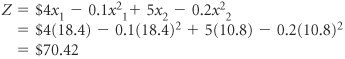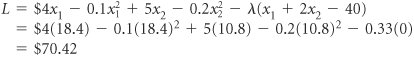The Method of Lagrange Multipliers

[Page D-4 ( continued )]

The method of Lagrange multipliers is a general mathematical technique that can be used for solving constrained optimization problems consisting of a nonlinear objective function and one or more linear or nonlinear constraint equations. In this method, the constraints as multiples of a Lagrange multiplier , l , are subtracted from the objective function.

In the method of Lagrange multipliers , constraints as multiples of a multiplier, l , are subtracted from the objective function, which is then differentiated with respect to each variable and solved .

To demonstrate this method, we will use our modified pottery company example developed in the preceding section. This model was formulated as

maximize Z = 4 x ₁ 0.1 x ² ₁ + 5 x ₂ 0.2 x ² ₂

subject to

x ₁ + 2 x ₂ = 40

The first step is to transform the nonlinear objective function into a Lagrangian function . This is accomplished by transforming the constraint equation as follows .

x ₁ + 2 x ₂ 40 = 0

Next, this expression is multiplied by l the Lagrangian multiplier , and subtracted from the objective function to form the Lagrangian function L.

L = 4 x ₁ 0.1 x ² ₁ + 5 x ₂ 0.2 x ² ₂ l ( x ₁ + 2 x ₂ 40)

---

[Page D-5]

Because the constraint equation now equals zero, the subtraction of the constraint, multiplied by l , from the objective function does not affect the value of the function. (We will explain the exact meaning of l after a solution has been determined.)

Now we must determine the partial derivatives of the Lagrangian function with respect to each of the three variables , x ₁ , x ₂ , and l .

The Lagrangian function is differentiated with respect to each variable, and the resulting equations are solved simultaneously .

These three equations are all set equal to zero and solved simultaneously to determine the values of x ₁ , x ₂ , and l .

To solve these equations simultaneously, we multiply the first equation by 2 and add it to the second equation, which eliminates l .

This new equation and the original preceding third equation represent two equations with two unknowns ( x ₁ and x ₂ ). We multiply the preceding third equation by 0.4 and add it to the new equation in order to eliminate x ₁ .

The resulting equation is solved for x ₂ as follows.

Substituting this value back into the previous equations gives the values of both x ₁ and l .

Substituting the values for x ₁ and x ₂ into the original objective function yields the total profit.

---

[Page D-6]

This result can also be obtained by using the Lagrangian function, L , and multiplier, l .

To summarize, we have x ₁ = 18.4 bowls, x ₂ = 10.8 mugs, Z = $70.42, and l = 0.33. This is the same answer obtained previously using the substitution method. However, unlike the substitution method, the Lagrange multiplier approach can be used to solve nonlinear programming problems with more complex constraint equations and inequality constraints . In addition, it can encompass problems with more than two variables. We will not pursue any examples, though, that demonstrate the complexities involved. The Lagrange multiplier method must be altered to compensate for inequality constraints and additional variables, and the resulting mathematics are very difficult. Even though the Lagrange multiplier method is more flexible than the substitution method, it is practical for solving only small problems. As the size of the problem increases , the mathematics become overwhelmingly difficult.

The Meaning of l

The Lagrange multiplier, l , in nonlinear programming problems is analogous to the dual variables in a linear programming problem. It reflects the approximate change in the objective function resulting from a unit change in the quantity (right-hand-side) value of the constraint equation. For our example, we will increase the quantity value in the constraint equation from 40 to 41 hours of labor. (You will recall from the preceding calculations that l = 0.33.)

The Lagrange multiplier, l , reflects a change in the objective function from a unit change in the right-hand-side value of a constraint .

x ₁ + 2 x ₂ = 41 or x ₁ + 2 x ₂ 41 = 0

This constraint equation will result in the following Lagrangian function.

L = 4 x ₁ 0.1 x ² ₁ + 5 x ₂ 0.2 x ² ₂ l ( x ₁ + 2 x ₂ 41)

Solving this problem the same way we solved the original model gives the following solution.

x ₁ = 18.7

x ₂ = 11.2

l = 0.27

Z = $70.75

This value for Z is $0.33 greater than the previous Z value of $70.42. Thus, a oneunit increase in the right-hand side of the constraint equation results in a l increase in the objective function. More specifically , a unit increase in a resource (labor) results in a $0.33 increase in profit. Thus, we would be willing to pay $0.33 for one additional hour of labor. This is the same interpretation as that given for a dual variable in linear programming.

In general, if l is positive, the optimal objective function value will increase if the quantity (absolute) value in the constraint equation is increased, and it will decrease if the quantity (absolute) value is decreased. On the other hand, if l is negative, the optimal objective function value will increase if the quantity (absolute) value is decreased, and it will decrease if the quantity (absolute) value is increased.