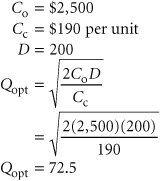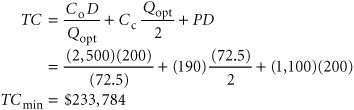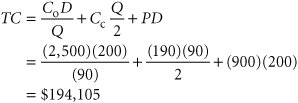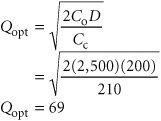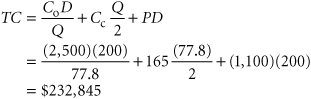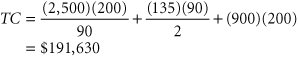Quantity Discounts
Quantity DiscountsIt is often possible for a customer to receive a price discount on an item if a predetermined number of units is ordered. For example, occasionally in the back of a magazine you might see an advertisement for a firm that will produce a coffee mug (or hat) with a company or organizational logo on it, and the price will be $5 per mug if you purchase 100, $4 per mug if you purchase 200, or $3 per mug if you purchase 500 or more. Many manufacturing companies receive price discounts for ordering materials and supplies in high volume, and retail stores receive price discounts for ordering merchandise in large quantities . The basic EOQ model can be used to determine the optimal order size with quantity discounts; however, the application of the model is slightly altered . The total inventory cost function must now include the purchase price for the order, as follows : where P = per unit price of the item D = annual demand Determining whether an order size with a discount is more cost-effective than optimal Q . Purchase price was not considered as part of our basic EOQ formulation earlier because it had no real impact on the optimal order size. PD in the foregoing formula is a constant value that would not alter the basic shape of the total cost curve (i.e., the minimum point on the cost curve would still be at the same location, corresponding to the same value of Q ). Thus, the optimal order size will be the same, no matter what the purchase price. However, when a discount price is available, it is associated with a specific order size that may be different from the optimal order size, and the customer must evaluate the trade-off between possibly higher carrying costs with the discount quantity versus EOQ cost. As a result, the purchase price does influence the order size decision when a discount is available. Quantity discounts can be evaluated using the basic EOQ model under two different scenarioswith constant carrying costs and with carrying costs as a percentage of the purchase price. It is not uncommon for carrying costs to be determined as a percentage of purchase price, although it was not considered as such in our previous basic EOQ model. Carrying cost very well could have been a percentage of purchase price, but it was reflected as a constant value, C c , in the basic EOQ model because the purchase price was not part of the EOQ formula. However, in the case of a quantity discount, carrying cost will vary with the change in price if it is computed as a percentage of purchase price. Quantity discounts are evaluated with constant C c and as a percentage of price . Quantity Discounts with Constant Carrying CostsIn the EOQ cost model with constant carrying costs, the optimal order size, Q opt , is the same, regardless of the discount price. Although total cost decreases with each discount in price because ordering and carrying cost are constant, the optimal order size, Q opt , does not change. The total cost with Q opt must be compared with any lower total cost with a discount price to see which is the minimum. The following example will illustrate the evaluation of an EOQ model with a quantity discount when the carrying cost is a constant value. Comptek Computers wants to reduce a large stock of personal computers it is discontinuing. It has offered the University Bookstore at Tech a quantity discount pricing schedule if the store will purchase the personal computers in volume, as follows:
The annual carrying cost for the bookstore for a computer is $190, the ordering cost is $2,500, and annual demand for this particular model is estimated to be 200 units. The bookstore wants to determine whether it should take advantage of this discount or order the basic EOQ order size. First, determine both the optimal order size and the total cost by using the basic EOQ model: This order size is eligible for the first discount of $1,100; therefore, this price is used to compute total cost, as follows: Because there is a discount for an order size larger than 72.5, this total cost of $233,784 must be compared with total cost with an order size of 90 and a price of $900, as follows: Because this total cost is lower ($194,105 < $233,784), the maximum discount price should be taken and 90 units ordered. Quantity Discounts with Constant Carrying Costs as a Percentage of PriceThe difference between the model in the previous section and the quantity discount model with carrying cost as a percentage of price is that there is a different optimal order size, Q opt , for each price discount. This requires that the optimal order size with a discount be determined a little differently from the case for a constant carrying cost. The optimal order size and total cost are determined by using the basic EOQ model for the case with no quantity discount. This total cost value is then compared with the various discount quantity order sizes to determine the minimum cost order size. However, once this minimum cost order size is determined, it must be compared with the EOQ-determined order size for the specific discount price because the EOQ order size, Q opt , will change for every discount level. Reconsider our previous example, except now assume that the annual carrying cost for a computer at the University Bookstore is 15% of the purchase price. Using the same discount pricing schedule, determine the optimal order size. The annual carrying cost is determined as follows:
C o = $2,500 D = 200 computers per year First, compute the optimal order size for the purchase price without a discount and with C c = $210, as follows: Because this order size exceeds 49 units, it is not feasible for this price, and a lower total cost will automatically be achieved with the first price discount of $1,100. However, the optimal order size will be different for this price discount because carrying cost is no longer constant. Thus, the new order size is computed as follows: This order size is the true optimum for this price discount instead of the 50 units required to receive the discount price; thus, it will result in the minimum total cost, computed as follows:
This cost must still be compared with the total cost for lowest discount price ($900) and order quantity (90 units), computed as follows: Because this total cost is lower ($191,630 < $232,845), the maximum discount price should be taken and 90 units ordered. However, as before, we still must check to see whether there is a new optimal order size for this discount that will result in an even lower cost. The optimal order size with C c = $135 is computed as follows: Because this order size is less than the 90 units required to receive the discount, it is not feasible; thus, the optimal order size is 90 units. Quantity Discount Model Solution with QM for WindowsQM for Windows has the capability to perform EOQ analysis with quantity discounts when carrying costs are constant. Exhibit 16.4 shows the solution summary for our University Bookstore example. Exhibit 16.4.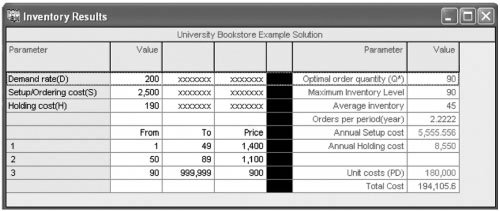 Quantity Discount Model Solution with ExcelIt is also possible to use Excel to solve the quantity discount model with constant carrying costs. Exhibit 16.5 shows the Excel solution screen for the University Bookstore example. Notice that the selection of the appropriate order size, Q , that results in the minimum total cost for each discount range is determined by the formulas embedded in cells E8, E9, and E10. For example, the formula for the first quantity discount range, 149, is embedded in cell E8 and shown on the formula bar at the top of the screen, = IF(D8>=B8,D8,B8) . This means that if the discount order size in cell D8 (i.e., Q = 72.55) is greater than or equal to the quantity in cell B8 (i.e., 1), the quantity in cell D8 (72.55) is selected; otherwise , the amount in cell B8 is selected. The formulas in cells E9 and E10 are constructed similarly. The result is that the order quantity for the final discount range, Q = 90, is selected. Exhibit 16.5.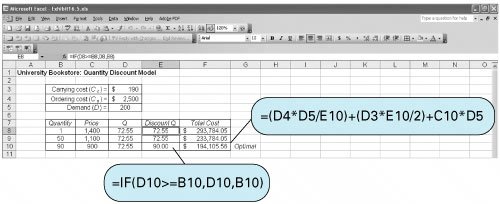 |
EAN: 2147483647
Pages: 358