12.6 Derivative pricing
12.6 Derivative pricing
Let us consider a cap on the forward LIBOR rate. Settlement is in arrears at times T j , j = 1, , n , with cash flows at time T j equal to ( L ( T j ˆ’ 1 , T j ˆ’ 1 ) ˆ’ ) + for each j = 1, , n , where is the strike price of the cap. Consider the cap price at time t , t ‰ T . By the risk-neutral valuation principle, the arbitrage-free price is given by:
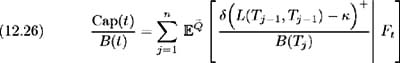
From (12.17) we have:
and so:
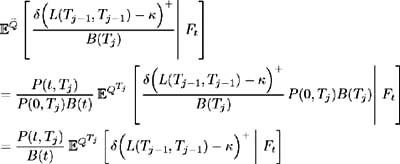
Substituting into (12.26) the cap price may be written as:
where each cash flow is valued under the forward measure corresponding to payment date T j . Here ![]() [ ·] denotes expectation under the time T j forward measure Q T j . This forward measure is defined, using (12.15), as:
[ ·] denotes expectation under the time T j forward measure Q T j . This forward measure is defined, using (12.15), as:
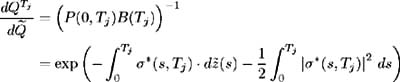
From (12.22) we know L ( t, T j ) may be represented as a lognormal martingale under the forward measure Q T j +1 ; hence:
and so given the time t forward value of the time T j LIBOR rate we have:
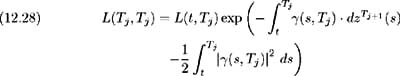
Now consider the process followed by ![]() . By Ito's Lemma we have:
. By Ito's Lemma we have:
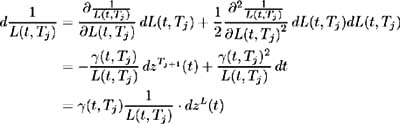
where
is the Brownian motion corresponding to probability measure Q L under which ![]() is a lognormal martingale. By the Girsanov Theorem, the Radon- Nikodym derivative defining this change of measure may be expressed as:
is a lognormal martingale. By the Girsanov Theorem, the Radon- Nikodym derivative defining this change of measure may be expressed as:
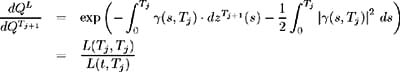
This change of measure affects the drift but not the volatility coefficient, hence as in (12.28) we may write:
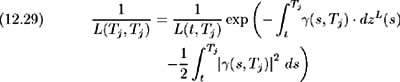
From (12.27) we see that the cap is made up of a series of n call options on LIBOR, or caplets, maturing at times T j , j = 1, , n respectively. Consider the value of a caplet with cash flow occurring at time T j +1 :
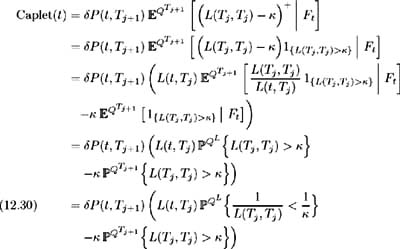
Hence, making use of (12.29) we have:

where
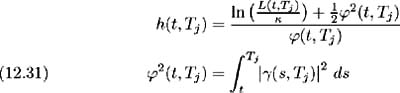
Similarly, making use of (12.28), we have:
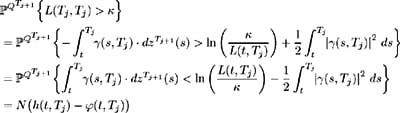
Substituting these results into (12.30), the time t value of a caplet with cash flow at time T j +1 may be written as:
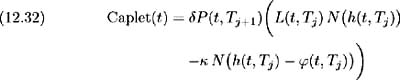
and so, by equation (12.27) the time t value of the entire cap is:
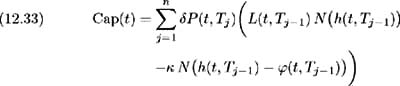
EAN: 2147483647
Pages: 132