12.5 Forward LIBOR rate with respect to the forward measure
12.5 Forward LIBOR rate with respect to the forward measure
Consider (12.10), the LIBOR rate process represented in terms of the ( T + )-maturity bond price volatility:
We may introduce a new n -dimensional process z T + ( t ) corresponding to time T + where
and a corresponding probability measure Q T + , equivalent to ![]() , under which z T + ( t ) is a Brownian motion. By (12.15), this new probability measure, called the forward measure, may be defined as:
, under which z T + ( t ) is a Brownian motion. By (12.15), this new probability measure, called the forward measure, may be defined as:
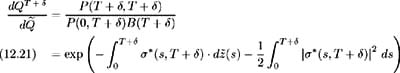
Now, considering (12.19) and making use of (12.20) we have:
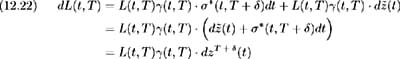
Hence each forward LIBOR rate L ( t, T ) follows a lognormal martingale process under the forward measure corresponding to its settlement date T + .
Using a forward measure for a date other than the settlement date, will require a drift adjustment. Consider (12.11), the LIBOR rate process expressed in terms of the T -maturity bond price volatility:
Making use of (12.20) and (12.21), we define the Brownian motion and forward probability measure corresponding to time T , the expiry date of the forward LIBOR rate, as:
and
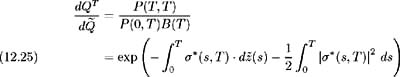
respectively, and so (12.23) becomes:
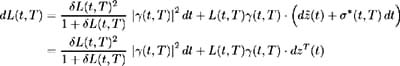
where ![]() ³ ( t, T ) 2 is the drift adjustment required when a forward measure corresponding to the expiry date of LIBOR is used. Making use of the recursive relationship of bond price volatilities shown in (12.9) and (12.12), the drift adjustment for any forward measure may be found. Equation (12.13) shows the drift adjustment when the spot measure is used. This corresponds to the money market account as numeraire and hence may be viewed as the time t measure. From this we may conclude that under this spot measure, no forward LIBOR rate follows a lognormal martingale.
³ ( t, T ) 2 is the drift adjustment required when a forward measure corresponding to the expiry date of LIBOR is used. Making use of the recursive relationship of bond price volatilities shown in (12.9) and (12.12), the drift adjustment for any forward measure may be found. Equation (12.13) shows the drift adjustment when the spot measure is used. This corresponds to the money market account as numeraire and hence may be viewed as the time t measure. From this we may conclude that under this spot measure, no forward LIBOR rate follows a lognormal martingale.
EAN: 2147483647
Pages: 132