Cryptography: Theory and Practice:Classical Cryptography | Modern Cryptography: Theory and Practice

Cryptography: Theory and Practice
by Douglas Stinson
CRC Press, CRC Press LLC
ISBN: 0849385210 Pub Date: 03/17/95

Table of Contents

1.2.3 Cryptanalysis of the Vigenere Cipher

In this section we describe some methods for cryptanalyzing the Vigenere Cipher. The first step is to determine the keyword length, which we denote by m. There are a couple of techniques that can be employed. The first of these is the so-called Kasiski test and the second uses the index of coincidence.

The Kasiski test was first described by Friedrich Kasiski in 1863. It is based on the observation that two identical segments of plaintext will be encrypted to the same ciphertext whenever their occurrence in the plaintext is x positions apart, where x ≡ 0 mod m. Conversely, if we observe two identical segments of ciphertext, each of length at least three, say, then there is a good chance that they do correspond to identical segments of plaintext.

The Kasiski test works as follows. We search the ciphertext for pairs of identical segments of length at least three, and record the distance between the starting positions of the two segments. If we obtain several such distances d₁, d₂, . . . , then we would conjecture that m divides the greatest common divisor of the d_i′s.

Further evidence for the value of m can be obtained by the index of coincidence. This concept was defined by Wolfe Friedman in 1920, as follows.

DEFINITION 1.7 Suppose x = x₁x₂ . . . x_n is a string of n alphabetic characters. The index of coincidence of x, denoted I_c(x), is defined to be the probability that two random elements of x are identical. Suppose we denote the frequencies of A, B, C, . . . , Z in x by f₀, f₁, . . . , f₂₅ (respectively). We can choose two elements of x in ways.² For each i, 0 ≤ i ≤ 25, there are 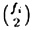ways of choosing both elements to be i. Hence, we have the formula

²The binomial coefficient = n!/(k!(n - k)!) denotes the number of ways of choosing a subset of k objects from a set of n objects.

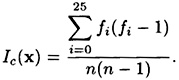
Now, suppose x is a string of English language text. Denote the expected probabilities of occurrence of the letters A, B, . . . , Z in Table 1.1 by p₀, . . . , p₂₅.

Then, we would expect that

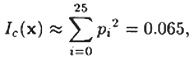
since the probability that two random elements both are A is p₀², the probability that both are B is p₁², etc. The same reasoning applies if x is a ciphertext obtained by means of any monoalphabetic cipher. In this case, the individual probabilities will be permuted, but the quantity

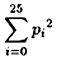
will be unchanged.

Now, suppose we start with a ciphertext y = y₁y₂ . . . y_n that has been constructed by using a Vigenere Cipher. Define m substrings y₁, y₂, . . . , y_m of y by writing out the ciphertext, by columns, in a rectangular array of dimensions m × (n/m). The rows of this matrix are the substrings y_i, 1 ≤ i ≤ m. If this is done, and m is indeed the keyword length, then each I_c(y_i) should be roughly equal to 0.065. On the other hand, if m is not the keyword length, then the substrings y_i will look much more random, since they will have been obtained by shift encryption with different keys. Observe that a completely random string will have

The two values 0.065 and 0.038 are sufficiently far apart that we will often be able to determine the correct keyword length (or confirm a guess that has already been made using the Kasiski test).

Let us illustrate these two techniques with an example.

Example 1.11

Ciphertext obtained from a Vigenere Cipher

               CHREEVOAHMAERATBIAXXWTNXBEEOPHBSBQMQEQERBW               RVXUOAKXAOSXXWEAHBWGJMMQMNKGRFVGXWTRZXWIAK               LXFPSKAUTEMNDCMGTSXMXBTUIADNGMGPSRELXNJELX               VRVPRTULHDNQWTWDTYGBPHXTFALJHASVBFXNGLLCHR               ZBWELEKMSJIKNBHWRJGNMGJSGLXFEYPHAGNRBIEQJT               AMRVLCRREMNDGLXRRIMGNSNRWCHRQHAEYEVTAQEBBI               PEEWEVKAKOEWADREMXMTBHHCHRTKDNVRZCHRCLQOHP               WQAIIWXNRMGWOIIFKEE

First, let’s try the Kasiski test. The ciphertext string CHR occurs in five places in the ciphertext, beginning at positions 1, 166, 236, 276 and 286. The distances from the first occurrence to the other three occurrences are (respectively) 165, 235, 275 and 285. The gcd of these four integers is 5, so that is very likely the keyword length.

Let’s see if computation of indices of coincidence gives the same conclusion. With m = 1, the index of coincidence is 0.045. With m = 2, the two indices are 0.046 and 0.041. With m = 3, we get 0.043, 0.050, 0.047. With m = 4, we have indices 0.042, 0.039, 0.046, 0.040. Then trying m = 5, we obtain the values 0.063, 0.068, 0.069, 0.061 and 0.072. This also provides strong evidence that the keyword length is five.

Proceeding under this assumption, how do we determine the keyword? It is useful to consider the mutual index of coincidence of two strings.

Table of Contents