GRAPHICAL PRESENTATIONS | Six Sigma and Beyond: Statistical Process Control, Volume IV

Where frequency distributions are constructed primarily to condense large sets of data and display them in an easy to digest form, it is usually advisable to present them graphically, that is, in a form that appeals to the human power of visualization. The most common among all graphical presentations of statistical data is the histogram. An example of our previous data in the form of a histogram is in Figure 3.3.

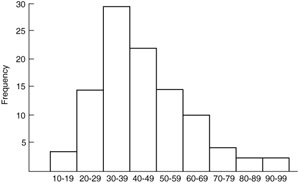
Figure 3.3: An example of a histogram showing the data of the starter motor.

A histogram is constructed by representing the measurements of observations that are grouped on the horizontal scale and the class frequency on the vertical scale.

Once the scales have been identified, then begins the drawing of the rectangles whose bases equal the class interval and whose heights are determined by the corresponding class frequencies. The markings on the horizontal scale can be the class limits, as in our example; the class boundaries; the class marks; or arbitrary key values. For easy readability, it is generally preferable to indicate the class limits, although the rectangles actually go from one class boundary to the next . Histograms cannot be used in connection with frequency distributions having open classes, and they must be used with extreme care if the classes are not all equal.

An alternative, though less widely used, form of graphical presentation is the frequency polygon. An example of a frequency polygon is shown in Figure 3.4.

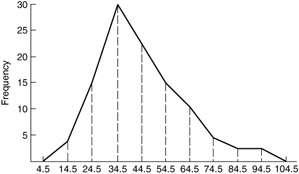
Figure 3.4: A frequency polygon.

Here, the class frequencies are plotted at the class marks, and the successive points are connected by means of straight lines. If we apply this same technique to a cumulative distribution, we obtain a so-called Ogive curve. The Ogive corresponds to the "or-less" principle, and an example based on our earlier data is shown in Figure 3.5.

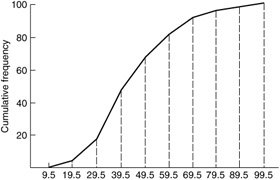
Figure 3.5: The Ogive curve.

DOT PLOTS

The dot diagram is a valuable device for displaying the distribution of a small body of data (up to about 20). In particular, it shows the general location of the observations and their spread.

A comparison with the histogram will identify the following characteristics of dot plots:

Whereas the histogram groups the data into just a few intervals, the dot plot groups the data as little as possible. Ideally, if we had wider paper or a printer with higher resolution, we would not group the data at all.
Whereas the histogram tends to be more useful with a large database, the dot plot is useful with a small database.
Whereas the histogram shows the shape of the distribution, the dot plot does not.

In the final analysis, dot plots are very useful if you want to compare two or more sets of data for location and spread. A typical dot plot is shown in Figure 3.6.

Figure 3.6: A typical dot plot.

To construct a dot plot, draw the x axis with the value scale of your choice, and then plot your observations.

STEM AND LEAF DISPLAYS

A stem and leaf display is a variation of the histogram and the check sheet. Although it was designed by J. Tukey in the late 1960s for variable data, it may be used with any set of numbers . A typical stem and leaf display is shown in Figure 3.7; this one uses the data from the starter motor in the discussion earlier in this chapter of the histogram.

Figure 3.7: A typical stem and leaf display.

The reader will notice that the shapes are very similar, with two major differences:

Whereas the histogram deals in intervals, the stem and leaf depends on the actual data to generate the distribution. The advantage of this is that the experimenter knows exactly where the data are coming from.
Whereas the scale for the intervals is on the x axis on the histogram, in the stem and leaf display, it is on the vertical side.

In evaluating Figure 3.7, we see that the numbers are to the left and to the right of a vertical line. The numbers to the left are called stems , and the numbers to the right are called leaves . To actually do the display, we must split the raw data into two parts (that is what the vertical line is all about). The split is usually between the tens digit, which becomes the stem, and the ones digit, which becomes the leaf. (If the data have more than two digits, you still split the numbers according to your requirements. For example, if you have three-digit numbers, say one of the numbers is 302, your stem may be 3 or 30, and the leaf may be 02 or 2, respectively. The reader will notice that if the stem in this case is identified as 3, the experimenter must be very cautious in the interpretation. We suggest that the stem be identified as the number that will cause the least confusion. In this case, we would recommend that the 30 be the stem and 2 be the leaf.)

The reader will also notice that the readings are the actual measurement and that the leaves always correspond to the individual stem from which they came. In our example, the stem that is one has three leaves. If you go back to the raw data, you will notice that indeed, the actual readings were 15, 16, and 19. We can do that for all the stems. In fact, Figure 3.7 gives the stem and leaf display for all 100 measurements of the data that we used to draw the histogram. The reader may want to compare the two.

BOX PLOTS

Yet another easy and effective way to summarize data is through a box plot. Box plots can be used in two different ways: either to describe a single variable in a data set or to compare two or more variables (see Figure 3.8). In Figure 3.8a, we show a box plot for a single variable, and in Figure 3.8b we show a box plot with three comparisons.

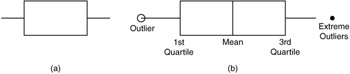
Figure 3.8: Typical box plots.

The keys to understanding a box plot are the following:

The right and left of the box are at the third and first quartiles. Therefore, the length of the box equals the interquartile range (IQR), and the box itself represents the middle 50% of the observations. The height of the box has no significance.
The vertical line inside the box indicates the location of the median. The point inside the box indicates the location of the mean.
Horizontal lines are drawn from each side of the box. They extend to the most extreme observations that are no further than 1.5 IQRs from the box. They are useful for indicating variability and skewness .
Observations farther than 1.5 IQRs from the box are shown as individual points. If they are between 1.5 IQRs and 3 IQRs from the box, they are called mild outliers and are hollow. Otherwise, they are called extreme outliers and are solid. (This convention was instituted by the statistician J. Tukey in the late 1960s and is still current.)

Box plots are not usually used as part of the basic SPC; however, they are used extensively in ANOVA and advanced SPC.

SCATTER DIAGRAMS

When one is interested in the relationship between the dependent variable and the independent variable, or merely between cause and effect, one may employ a scatter diagram. A scatter diagram is a grouping of plotted points on a two-axis graph. Usually, the two axes are the x axis and y axis. These plotted points form a pattern that indicates whether there is any connection between the two variables. The major objective in making a scatter diagram is to find out whether there is a relationship (correlation) between the variables under study and, if there is, how much one variable influences the other.

By finding out whether one variable influences another and the extent of that influence, one can infer that a cause and effect relationship exists and take appropriate measures to rectify the causal variable.

Scatter diagram construction involves the following steps:

Select two variables that seem to relate in a cause and effect relationship. This can be based on experiences or theory. For example, the grind bearing diameter seems to vary as different speeds are used in the grinders. Here, the cause would seem to be the speed, and the undesirable effect, to be a varying diameter.
Construct a vertical axis that will encompass all the values that you have obtained for the diameter. Similarly, construct a horizontal axis that represents all the measured values for the speeds (see Figure 3.9). Figure 3.9a shows the two axes for constructing the scatter diagram; Figure 3.9b shows the points plotted and their relationship to each other. Figure 3.9c shows a typical scatter diagram with positive correlation between two variables. Figure 3.9d shows a typical scatter diagram with no relationship between two variables. Figure 3.9e shows a typical scatter diagram with negative correlation between two variables. Finally, Figures 3.9f and 3.9g show a possible positive and a possible negative correlation between two variables, respectively.

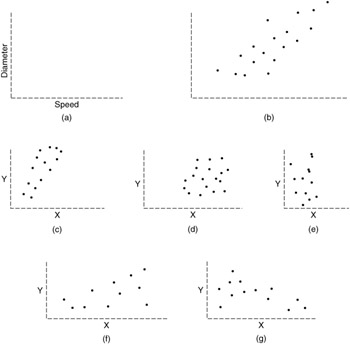
Figure 3.9: Scatter diagrams.
Plot all the measured values for the diameters and the speeds (Figure 3.9b).

Reading Scatter Diagrams

In Figure 3.9b, one can see that as the speed increases, the diameter also increases . In this case, the scatter diagram shows that a relationship exists between the two variables. In fact, one may be tempted to say that one causes the other to change. Knowing this, one can proceed to control the apparent causal variable ”grinder speed ”and be assured that the diameter will also be controlled to some extent the same way. (Even though it is tempting to think of the existence of a definite cause at this stage, the scatter diagram does not provide us with a strong and irrefutable answer as to any cause. The best it offers is a relationship. Period!)

Scatter diagrams can be varied. The way that the plotted points fall depends on the collected data. The shape and the direction of that shape, however, determines whether the two variables have a relation at all and, if so, what the relation is and how strong it is. The basic shapes of the scatter diagram are as follows .

Positive correlation: Figure 3.9c is a scatter diagram showing positive correlation between two variables. This diagram shows a distinct, positive relationship between X and Y as mentioned earlier; that means that as X increases, so does Y. Or, if one of these variables were controlled, the other one would also be controlled.

A comment about the scatter diagram is necessary here. That is, the closeness of the plotted points indicates the degree of the relationship between the variables. To facilitate this closeness, imagine a line that is drawn between all the points. Such a line will have half of the points on one side and half on the other side. As the points fall close to the line on either side, as in this case, we say that X will quite accurately predict the value of Y. As the points scatter about, then our prediction becomes less accurate. This line turns out to be the correlation line, or regression line; the method of calculation was shown in Volume III.

No relationship: In Figure 3.9d, the scatter diagram shows no relationship. That means that given our data, we cannot show a relationship.

Points that seem to fall all over the two-axes plot or to form a circular pattern indicate that the two variables do not influence one another. That means that as we move or change one variable, the change in the other is not predictable. We conclude in such a situation that the two chosen variables are independent of each other and that some other variable (cause) must be found that influences the variable Y (effect).

Negative relationship: In Figure 3.9e, the scatter diagram shows negative correlation. If the points form a tight pattern about an imaginary line and the direction of that line is from the upper left of the diagram to the lower right of the diagram, then we say that there is a definite relationship between X and Y, such that if one variable changes in one direction, the other one will change in the opposite direction. This kind of relationship between two variables is called a negative correlation, and it implies that, indeed, there exists a cause and effect relationship between the two variables.

Possible positive and negative correlation: When the points are dispersed about the imaginary line but that dispersion is in a pattern such that a direction is visible but a definite causation is not determined, then we say either that a possible positive relationship exists or that a possible negative relationship exists. This means that depending on the direction of the imaginary line, one can say that changes in X will produce changes in Y; however, these changes will not necessarily be equal. Of importance in these possible relationships is the fact that X does have some influence on how Y will change but that other factors are present that will also influence how Y changes.

In Figures 3.9f,g, the scatter diagrams show possible positive correlation and possible negative correlation, respectively. The reader will notice here that the slope (pitch) of the imaginary line is not as steep as that indicating the positive or the negative correlation in Figures 3.9c,e.

An alternative way to look for a correlation with the scatter plot is the following approach:

Plot the data in the normal way (as discussed earlier).
Count the total points ( N ).
Draw a vertical median line such that half of the points are on the left side of the line and half of the points are on the right side of the line.
Draw a horizontal median line such that half of the points are above the line and half of the points are below the line.
Count the number of points in each quadrant.
Add the number of points in diagonally opposite quadrants as follows:

Look up the total number of points, N, in Table 3.2. Compare the smaller of the two sums calculated in step 6 to the critical value in the table. A significant correlation exists if smaller sum ‰ critical value. The critical values for a 95% confidence interval are shown in Table 3.2.

Table 3.2: Critical Values at 95% Confidence That a Significant Correlation Exists
N	I + III OR II + IV
20	5
21	5
22	5
23	6
24	6
25	7
26	7
27	7
28	8
29	8
30	9
31	9
32	9
33	10
34	10
35	11
36	11
37	12
38	12
39	12
40	13
41	13
42	14
43	14
44	15
45	15
46	15
47	16
48	16
49	17
50	17
51	18
52	18
53	18
54	19
55	19
56	20
57	20
58	21
59	21
60	21
61	22
62	22
63	23
64	23
65	24
66	24
67	25
68	25
69	25
70	26
71	26
72	27
73	27
74	28
75	28
76	28
77	29
78	29
79	30
80	30

If we are interested in a more sophisticated way to identify the relationship, then we may use a correlation or even a multiple correlation analysis (see Volume III). We may want to consider correlation if any of the following conditions are present:

Many variables change simultaneously .
Variables have complicated effects:
- Nonlinear
- Interaction between variables
Unexplained or random variation is high.
Accurate predictions are necessary for optimization.
Need to know which variables are important and which are not.
Fortuitous variables are present.
No information on important variables.
Oddball results.

Even though correlation is indeed a very powerful tool, the truth of the matter is that in basic analysis, the scatter plot is just as good. For elementary analysis, if we were to experiment with "correlation" proper, we should also be aware of its pitfalls and difficulties. Some are identified below:

One has to deal with many variables.
Variables may change constantly.
Nonlinear effects must be accounted for.
Interaction effects must be accounted for.
Experimental error must be understood and accounted for.
Variable changes are small.
Fortuitous variables may be present.
No information may be available on important variables.

It is because of these difficulties that correlation analysis is usually done by specialists and that for a basic analysis, the scatter plot is preferred.