5. Biased Discriminant Analysis

Instead of confining ourselves to the traditional settings of the discriminant analysis, a better way is to use a new form of the discriminant analysis, namely, our proposed biased discriminant analysis (BDA).

5.1 (1+x)-Class Assumption

We first define the (1+ x)-class classification problem or biased classification problem as the learning problem in which there are an unknown number of classes but the user is only interested in one class, i.e., the user is biased toward one class. And the training samples are labeled by the user as only "positive" or "negative" as to whether they belong to the target class or not. Thus, the negative examples can come from an uncertain number of classes.

Much research has addressed this problem simply as a two-class classification problem with symmetric treatment on positive and negative examples, such as FDA. However the intuition is like "all good marriages are good in a similar way, while all bad marriages are bad in their own ways"; or we say "all positive examples are good in the same way, while negative examples are bad in their own ways." Therefore, it is desirable to distinguish a real two-class problem from a (1+x)-class problem. When the negative examples are far from representing their true distributions, which is certainly true in our case, this distinction becomes critical. (Tieu and Viola [25] used a random sampling strategy to increase the number of negative examples and thus their representative power. This is somewhat dangerous since unlabeled positive examples can be included in these "negative" samples.)

5.2 BDA

For a biased classification problem, we ask the following question instead: What is the optimal discriminating subspace in which the positive examples are "pulled" closer to one another while the negative examples are "pushed" away from the positive ones?

Or mathematically: What is the optimal transformation such that the ratio of "the negative scatter with respect to positive centroid" over "the positive within class scatter" is maximized? We call this biased discriminant analysis (BDA) due to the biased treatment of the positive examples. We define the biased criterion function

(30.8)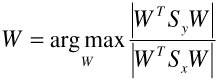

where

(30.9)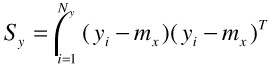

(30.10)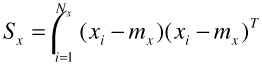

The optimal solution and transformations are of the same formats as those of FDA or MDA, subject to the differences defined by Equations (30.9) and (30.10).

Note that the discriminating subspace of BDA has an effective dimension of min{N_x, N_y}, the same as MDA and higher than that of FDA.

5.3 Regularization and Discounting Factors

It is well known that the sample-based plug-in estimates of the scatter matrices based on Equations (30.2)–(30.5), (30.9), and (30.10) will be severely biased for a small number of training examples, in which case regularization is necessary to avoid singularity in the matrices. This is done by adding small quantities to the diagonal of the scatter matrices. For detailed analysis see [44]. The regularized version of S_x, with n being the dimension of the original space and I being the identity matrix, is

(30.11)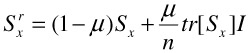

The parameter μ controls shrinkage toward a multiple of the identity matrix.

The influence of the negative examples can be tuned down by a discounting factor γ, and the discounted version of S_y is

(30.12)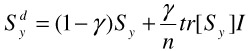

With different combinations of the (μ, γ) values, regularized BDA provides a fairly rich set of alternatives. The combination (μ = 0, γ = 1) gives a subspace that is mainly defined by minimizing the scatters among the positive examples, resembling the effect of a whitening transform. The combination (μ = 1, γ = 0) gives a subspace that mainly separates the negative from the positive centroid, with minimal effort on clustering the positive examples. The combination (μ = 0, γ = 0) is the full BDA and (μ = 1, γ = 1) represents the extreme of discounting all configurations of the training examples and keeping the original feature space unchanged.

BDA captures the essential nature of the problem with minimal assumption. In fact, even the Gaussian assumption on the positive examples can be further relaxed by incorporating kernels.

5.4 Discriminating Transform

Similar to FDA and MDA, we first solve for the generalized eigenanalysis problem with generalized square eigenvector matrix V associated with the eigenvalue matrix ʌ, satisfying

(30.13)

However, instead of using the traditional discriminating dimensionality reduction matrix in the form of Equation (30.7), we propose the discriminating transform matrix as

(30.14)

As for the transformation A, the weighting of different eigenvectors by the square roots of their corresponding eigenvalues in fact has no effect on the value of the objective function in Equation (30.8). But it will make a difference when a k-nearest neighbor classifier is to be applied in the transformed space.

5.5 Generalizing BDA

One generalization of BDA is to take in multiple positive clusters instead of one [45]. For example, the training set may be labeled as red horse, white horse, black horse, and non horse, then we shall formulate BDA such that red horses, white horses, and black horses all cluster within their own color, plus all non-horses are pushed away from these three. The definition of this generalized BDA will be similar to above, but we need to change equation (30.9) and (30.10) into equation (30.15) and (30.16) below.

(30.15)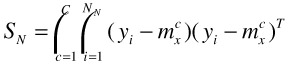

(30.16)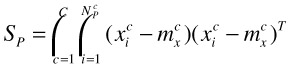

where C is the total number of clusters in positive examples, {}, i = 1,2,…, are the positive examples in cluster c, and is the mean vector of positive cluster c.

If the separation of different colored horses is important to the user, we can add the corresponding scatters into equation (30.15). Note this is not MDA since again it is "biased" toward horses: the scatter of non horses are not minimized.

This generalization is applicable if the user is willing to give clustering information on the positive examples, which might not be realistic in many applications.