5.4 Densities

---

5.4 Densities

A density function defines the derivative of the distribution function, indicating the rate of change of the probability distribution:

(5.46) 

This definition holds for continuous random variables. For discrete random variables, the density function is defined as the discrete probabilities that the random variable equals a specific value for its range of possible values. That is:

(5.47) 

where δ(x - X) is a delta function that is 1 when x = X and 0 elsewhere.

From the previous relationships, we can see how the distribution function is formed. For each value of the random variable, we can integrate (for a continuous function) up to that point to find the cumulative probability to that point. The probabilities are summed for discrete functions:

(5.48)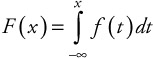 

(5.49)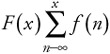 

We know from the previous discussions that F(∞) = 1, so that:

(5.50)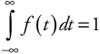 

and

(5.51)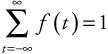 

In a manner similar to that shown previously for finding the distribution function from the density function for a single random variable, we can find the joint distribution from the joint density. The relationship is given by:

(5.52)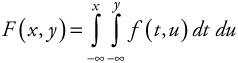 

Similarly, a discrete distribution can be found from the discrete density:

(5.53)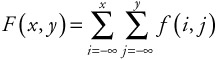 

As with singularly distributed densities, the total area under the probability density function is given by:

(5.54)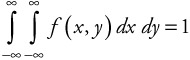 

Obtaining the density function from the distribution function for a continuous case is given by:

(5.55) 

We define the marginal density of a jointly distributed random variable as:

(5.56)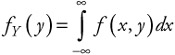 

The independence property is defined on joint distributions as:

(5.57) 

and for joint densities as:

(5.58) 

In some cases, it is necessary to define combined joint distributions in which one of the variables is discrete and the other continuous. The joint density, where y represents the continuous variable and i represents the discrete one, is written as:

(5.59) 

This expression introduces another important point: conditional distributions. For discrete random variables, the conditional function can be defined as the following:

(5.60) 

Similarly, we can define the conditional density of y given x from equation (5.60). The following results:

(5.61) 

This is a convenient way to relate the conditional densities for the two random variables. If the random variables X and Y are independent, equation (5.60) becomes:

(5.62) 

and the following results:

(5.63) 

From equations (5.56) and (5.60), we can substitute to get:

(5.64) 

and also (for the marginal density of X):

(5.65) 

Combining equations (5.60), (5.61), and (5.64), we obtain Bayes's rule for continuous random variables:

(5.66)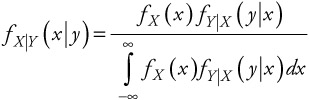 

This concludes our discussion about the properties of probability distributions and densities. In the next section, we will explore some methods for obtaining often used statistics about random variables by using their distributions and densities.

---