Back to the Tic-Tac-Toe Game

The Tic-Tac-Toe game presented at the beginning of the chapter is your most ambitious chapter project yet. You certainly have all the skills you need to create the game, but instead of jumping straight into the code, I'm going to go through a planning section to help you get the bigger picture and understand how to create a larger program.

Planning the Tic-Tac-Toe Game

If you haven't figured this out by now, I'll bore you with it again: the most important part of programming is planning to program. Without a roadmap, you'll never get to where you want to go (or it'll take you a lot longer as you travel the scenic route).

Writing the Pseudocode

It's back to your favorite language that's not really a language: pseudocode. Since I'll be using functions for most of the tasks in the program, I can afford to think about the program at a pretty abstract level. Each line of pseudocode should feel like one function call. Then, later, I'll just have to write the functions that the plan implies. Here's the pseudocode:

 display the game instructions determine who goes first create an empty tic-tac-toe board display the board while nobody's won and it's not a tie   if it's the human's turn       get the human's move       update the board with the move   otherwise     calculate the computer's move     update the board with the move   display the board   switch turns congratulate the winner or declare a tie 

Representing the Data

Alright, I have a good plan, but it is pretty abstract and talks about throwing around different elements that aren't really defined in my mind yet. I see the idea of making a move as placing a piece on a game board. But how exactly am I going to represent the game board? Or a piece? Or a move?

Since I'm going to print the game board on the screen, why not just represent a piece as one character, an "X" or an "O"? An empty piece could just be a space. The board itself should be a list since it's going to change as each player makes a move. There are nine squares on a tic-tac-toe board, so the list should be nine elements long. Each square on the board will correspond to a position in the list that represents the board. Figure 6.9 illustrates what I mean.

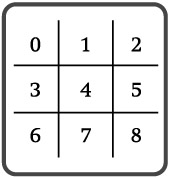
Figure 6.9: Each square number corresponds to a position in a list that represents the board.

So, each square or position on the board is represented by a number, 0–8. That means the list will be nine elements long and have position numbers 0–8. Since each move indicates a square in which to put a piece, a move is also just a number, 0–8.

The sides the player and computer play could also be represented by "X" and "O", just like a game piece. And a variable to represent the side of the current turn would be either an "X" or an "O".

Creating a List of Functions

The pseudocode inspires the different functions I'll need. I created a list of them, thinking about what they would do, what parameters they would have, and what values they would return. Table 6.1 shows the results of my efforts.

Table 6.1: TIC-TAC-TOE FUNCTIONS

Function	Description
display_instruct()	Displays the game instructions.
def ask_yes_no(question)	Asks a yes or no question. Receives a question. Returns either a "y" or a "n".
def ask_number(question, low, high)	Asks for a number within a range. Receives a question, a low number, and a high number. Returns a number in the range from low to high.
pieces()	Determines who goes first. Returns the computer's piece and human's piece.
new_board()	Creates a new, empty game board. Returns a board.
display_board(board)	Displays the board on the screen. Receives a board.
legal_moves(board)	Creates a list of legal moves. Receives a board. Returns a list of legal moves.
winner(board)	Determines the game winner. Receives a board. Returns a piece, "TIE" or None.
human_move(board, human)	Gets the human's move from the player. Receives a board and the human's piece. Returns the human's move.
computer_move(board, computer, human)	Calculates the computer's move. Receives a board, the computer piece, and the human piece. Returns the computer's move.
next_turn(turn)	Switches turns based on the current turn. Receives a piece. Returns a piece.
congrat_winner(the_winner, computer, human)	Congratulates the winner or declares a tie. Receives the winning piece, the computer's piece, and the human's piece.

Setting Up the Program

The first thing I did in writing the program was set up some global constants. These are values that more than one function will use. Creating them will make the functions clearer and any changes involving these values easier.

 # Tic-Tac-Toe # Plays the game of tic-tac-toe against a human opponent # Michael Dawson - 2/21/03 # global constants X = "X" O = "O" EMPTY = "" TIE = "TIE" NUM_SQUARES = 9 

X is just shorthand for "X", one of the two pieces in the game. O represents "O", the other piece in the game. EMPTY represents an empty square on the board. It's a space because when it's printed, it will look like an empty square. TIE represents a tie game. And NUM_SQUARES is the number of squares on the tic-tac-toe board.

The display_instruct() Function

This function displays the game instructions. You've seen it before:

 def display_instruct():     """ Display game instructions."""     print \     """     Welcome to the greatest intellectual challenge of all time: Tic-Tac-Toe.     This will be a showdown between your human brain and my silicon processor.     You will make your move known by entering a number, 0 - 8. The number     will correspond to the board position as illustrated:                      0 | 1 | 2                     -----------                      3 | 4 | 5                     -----------                      6 | 7 | 8     Prepare yourself, human. The ultimate battle is about to begin. \n     """ 

The only thing I did was change the function name for the sake of consistency in the program.

The ask_yes_no() Function

This function asks a yes or no question. It receives a question and returns either a "y" or a "n". You've seen this function before too.

 def ask_yes_no(question):     """ Ask a yes or no question."""     response = None     while response not in ("y", "n"):         response = raw_input(question).lower()     return response 

The ask_number() Function

This function asks for a number within a range. It receives a question, a low number, and a high number. It returns a number within the range specified.

 def ask_number(question, low, high):     """ Ask for a number within a range."""     response = None     while response not in range(low, high):         response = int(raw_input(question))     return response 

The pieces() Function

This function asks the player if he or she wants to go first and returns the computer's piece and human's piece, based on that choice. As the great tradition of tic-tac-toe dictates, the X's go first.

 def pieces():     """ Determine if player or computer goes first."""     go_first = ask_yes_no("Do you require the first move? (y/n): ")     if go_first == "y":         print "\nThen take the first move. You will need it."         human = X         computer = O     else:         print "\nYour bravery will be your undoing... I will go first."         computer = X         human = O     return computer, human 

Notice that this function calls another one of my functions, ask_yes_no(). This is perfectly fine. One function can call another.

The new_board() Function

This function creates a new board (a list) with all nine elements set to EMPTY and returns it:

 def new_board():     """ Create new game board."""     board = []     for square in range(NUM_SQUARES):         board.append(EMPTY)     return board 

The display_board() Function

This function displays the board passed to it. Since each element in the board is either a space, the character "X", or the character "O", the function can print each one. A few other characters on my keyboard are used to draw a decent-looking tic-tac-toe board.

 def display_board(board):     """ Display game board on screen."""     print "\n\t", board[0], "|", board[1], "|", board[2]     print "\t", "————-"     print "\t", board[3], "|", board[4], "|", board[5]     print "\t", "————-"     print "\t", board[6], "|", board[7], "|", board[8], "\n" 

The legal_moves() Function

This function receives a board and returns a list of legal moves. This function is used by other functions. It's used by the human_move() function to make sure that the player chooses a valid move. It's also used by the computer_move() function so that the computer can consider only valid moves in its decision making.

A legal move is represented by the number of an empty square. For example, if the center square were open, then 4 would be a legal move. If only the corner squares were open, the list of legal moves would be [0, 2, 6, 8]. (Take a look at Figure 6.9 if you're unclear about this.)

So, this function just loops over the list representing the board. Each time it finds an empty square, it adds that square number to the list of legal moves. Then it returns the list of legal moves.

 def legal_moves(board):     """ Create list of legal moves."""     moves = []     for square in range(NUM_SQUARES):         if board[square] == EMPTY:             moves.append(square)     return moves 

The winner() Function

This function receives a board and returns the winner. There are four possible values for a winner. The function will return either X or O if one of the players has won. If every square is filled and no one has won, it returns TIE. Finally, if no one has won and there is at least one empty square, the function returns None.

The very first thing I do in this function is define a constant called WAYS_TO_WIN, which represents all eight ways to get three in a row. Each way to win is represented by a tuple. Each tuple is a sequence of the three board positions that form a winning three in a row. Take the first tuple in the sequence, (0, 1, 2). This represents the top row: board positions 0, 1, and 2. The next tuple (3, 4, 5) represents the middle row. And so on.

 def winner(board):     """ Determine the game winner."""     WAYS_TO_WIN = ((0, 1, 2),                     (3, 4, 5),                     (6, 7, 8),                     (0, 3, 6),                     (1, 4, 7),                     (2, 5, 8),                     (0, 4, 8),                     (2, 4, 6)) 

Next, I use a for loop to go through each possible way a player can win, to see if either player has three in a row. The if statement checks to see if the three squares in question all contain the same value and are not empty. If so, that means that the row has either three X's or O's in it and somebody has won. The computer assigns one of the pieces in this winning row to winner, returns winner, and ends.

     for row in WAYS_TO_WIN:         if board[row[0]] == board[row[1]] == board[row[2]] != EMPTY:             winner = board[row[0]]             return winner 

If neither player has won, then the function continues. Next, it checks to see if there are any empty squares left on the board. If there aren't any, the game is a tie (because the function has already determined that there is no winner, back in the for loop) and TIE is returned.

     if EMPTY not in board:         return TIE 

If the game isn't a tie, the function continues. Finally, if neither player has won and the game isn't a tie, there is no winner yet. So, the function returns None.

     return None 

The human_move() Function

This next function receives a board and the human's piece. It returns the square number where the player wants to move.

First, the function gets a list of all the legal moves for this board. Then, it continues to ask the user for the square number to which he or she wants to move until that response is in this list of legal moves. Once that happens, the function returns the move.

 def human_move(board, human):     """ Get human move."""     legal = legal_moves(board)     move = None     while move not in legal:         move = ask_number("Where will you move? (0 - 8): ", 0, NUM_SQUARES)         if move not in legal:             print "\nThat square is already occupied, foolish human. Choose another.\n"     print "Fine.."     return move 

The computer_move() Function

The computer_move() function receives the board, the computer's piece, and the human's piece. It returns the computer's move.

TRICK

This is definitely the meatiest function in the program. Knowing it would be, I initially created a short, temporary function that chooses a random but legal move. I wanted time to think about this function, but didn't want to slow the progress of the entire project. So, I dropped in the temporary function and got the game up and running. Later, I came back and plugged in a better function that actually picks moves for a reason.

I had this flexibility because of the modular design afforded by writing with functions. I knew that computer_move() was a totally independent component and could be substituted later, without a problem. In fact, I could even drop a new function in right now, one that chooses even better moves. (Sounds an awful lot like a challenge, now doesn't it?)

I have to be careful here because the board (a list) is mutable and I change it in this function as I search for the best computer move. The problem with this is that any change I make to the board will be reflected in the part of the program that called this function. This is the result of shared references, which you learned about in Chapter 5 section "Understanding Shared References." Basically, there's only one copy of the list, and any change I make here changes that single copy. So, the very first thing I do is make my own, local copy to work with:

 def computer_move(board, computer, human):     """ Make computer move."""     # make a copy to work with since function will be changing list     board = board[:] 

HINT

Any time you get a mutable value passed to a function, you have to be careful. If you know you're going to change the value as you work with it, make a copy and use that instead.

TRAP

You might think that changing the board would be a good thing. You could change it so that it contains the new computer move. This way, you don't need to send the board back as a return value.

Changing a mutable parameter directly like this is considered creating a side effect. Not all side effects are bad, but this type is generally frowned upon (I'm frowning right now, just thinking about it). It's best to communicate with the rest of your program through return values; that way, it's clear exactly what information you're giving back.

Okay, here's the basic strategy I came up with for the computer:

1. If there's a move that allows the computer to win this turn, the computer should choose that move.

2. If there's a move that allows the human to win next turn, the computer should choose that move.

3. Otherwise, the computer should choose the best empty square as its move. The best square is the center. The next best squares are the corners. And the next best squares are the rest.

So next in the code, I define a tuple to represent the best squares, in order:

     # the best positions to have, in order     BEST_MOVES = (4, 0, 2, 6, 8, 1, 3, 5, 7)     print "I shall take square number", 

Next, I create a list of all the legal moves. In a loop, I try the computer's piece in each empty square number I got from the legal moves list and check for a win. If the computer can win, then that's the move to make. If that's the case, the function returns that move and ends. Otherwise, I undo the move I just tried and try the next one in the list.

     # if computer can win, take that move     for move in legal_moves(board):         board[move] = computer         if winner(board) == computer:             print move             return move         # done checking this move, undo it         board[move] = EMPTY 

If I get to this point in the function, it means the computer can't win on its next move. So, I check to see if the player can win on his or her next move. The code loops through the list of the legal moves, putting the human's piece in each empty square, checking for a win. If the human can win, then that's the move to take for a block. If this is the case, the function returns the move and ends. Otherwise, I undo the move and try the next legal move in the list.

    # if human can win, block that move    for move in legal_moves(board):        board[move] = human        if winner(board) == human:            print move            return move        # done checking this move, undo it        board[move] = EMPTY 

If I get to this point in the function, then neither side can win on its next move. So, I look through the list of best moves and take the first legal one. The computer loops through BEST_MOVES, and as soon as it finds one that's legal, it returns that move.

    # since no one can win on next move, pick best open square    for move in BEST_MOVES:        if move in legal_moves(board):            print move            return move 

IN THE REAL WORLD

The Tic-Tac-Toe program considers only the next possible move in the game. Programs that play serious games of strategy, like chess, look far deeper into the consequences of individual moves, considering many levels of moves and countermoves. And today's computers can examine a huge number of game positions. Specialized machines, like IBM's chess-playing Deep Blue computer, which beat world champion Garry Kasparov, can examine far more. Deep Blue is able to explore over 200,000,000 board positions per second. That sounds quite impressive, until you realize that the total number of board positions in a complete search for chess is estimated to be over 100,000, 000,000,000,000,000,000,000,000,000,000,000,000,000,000,000, which means it would take Deep Blue more than 1,585,489,599,188,229 years to look at all those possible positions. (The universe, by the way, is estimated to be only 15,000,000,000 years old.)

The next_turn() Function

This function receives the current turn and returns the next turn. A turn represents whose turn it is and is either X or O.

 def next_turn(turn):     """ Switch turns."""     if turn == X:         return O     else:         return X 

The function is used to switch turns after one player has made a move.

The congrat_winner() Function

This function receives the winner of the game, the computer's piece, and the human's piece. This function is called only when the game is over, so the_winner will be passed either X or O if one of the player's has won the game, or TIE if the game ended in a tie.

 def congrat_winner(the_winner, computer, human):     """ Congratulate the winner."""     if the_winner != TIE:         print the_winner, "won!\n"     else:         print "It's a tie!\n"     if the_winner == computer:         print "As I predicted, human, I am triumphant once more. \n" \               "Proof that computers are superior to humans in all regards."     elif the_winner == human:         print "No, no! It cannot be! Somehow you tricked me, human. \n" \               "But never again! I, the computer, so swears it!"     elif the_winner == TIE:         print "You were most lucky, human, and somehow managed to tie me. \n" \               "Celebrate today... for this is the best you will ever achieve." 

The main() Function

I put the main part of the program into its own function, instead of leaving it at the global level. This encapsulates the main code too. Unless you're writing a short, simple program, it's usually a good idea to encapsulate even the main part of it. If you do put your main code into a function like this, you don't have to call it main(). There's no magic to the name. But it's a pretty common practice, so it's a good idea to use it.

Okay, here's the code for the main part of the program. As you can see, it's almost exactly, line for line, the pseudocode I wrote earlier:

 def main():     display_instruct()     computer, human = pieces()     turn = X     board = new_board()     display_board(board)     while not winner(board):         if turn == human:             move = human_move(board, human)             board[move] = human         else:             move = computer_move(board, computer, human)             board[move] = computer         display_board(board)         turn = next_turn(turn)     the_winner = winner(board)     congrat_winner(the_winner, computer, human) 

Starting the Program

The next line calls the main function (which in turn calls the other functions) from the global level:

 # start the program main() raw_input("\n\nPress the enter key to quit.")