A.17 Lemma

< Free Open Study >

For any two μ-types S, T, if (S, T) Î vS_d, then (S,T) Î S_m(vS_d).

Proof sketch: By lexicographic induction on (n,k), where k = μ-height(S) and n = μ-height(T). This induction verifies the informal idea that any derivation of (S, T) Î vS_d can be transformed into another derivation of the same fact, that also happens to be a derivation of (S, T) Î vS_m. The restrictions in the rule of left μ-folding dictate that the transformed derivation has the property that every sequence of applications of μ-folding rules starts with a sequence of left μ-foldings, which are then followed by a sequence of right μ-foldings.

21.9.2 Solution

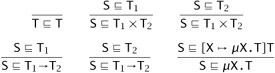
(Note, as a point of interest, that the generating function TD differs from the generating functions we have considered throughout this chapter: it is not invertible. For example, B ⊑ A×B→B × C is supported by the two sets {B ⊑ A × B} and {B ⊑ B × C}, neither of which is a subset of the other.)

21.9.7 Solution

All the rules for BU are the same as the rules for TD given in the solution of Exercise 21.9.2, except the rule for types starting with a μ binder:

21.11.1 Solution

There are lots. A trivial example is μX.T and [X ↦ μX.T]T for just about any T. A more interesting one is μX. Nat × (Nat × X) and μX. Nat × X.

22.3.9 Solution

Here are the main algorithmic constraint generation rules:

The remaining rules are similar. The equivalence of the original rules and the algorithmic presentation can be stated as follows:

(SOUNDNESS) If Г ⊢_F t : T |_F′ C and the variables mentioned in Г and t do not appear in F, then Г ⊢ t : T |_F\F′ C.
(COMPLETENESS) If Г ⊢ t : T |_X C, then there is some permutation F of the names in X such that Г ⊢_F t : T |_ C.

Both parts are proved by straightforward induction on derivations. For the application case in part 1, the following lemma is useful:

If the type variables mentioned in Г and t do not appear in F and if Г ⊢_F t : T |_F′ C, then the type variables mentioned in T and C do not appear in F \ F′.

For the corresponding case in part 2, the following lemma is used:

If Г⊢_F t : T |_F′ C, then Г ⊢_F,G t : T |_F′,G C, where G is any sequence of fresh variable names.

22.3.10 Solution

Representing constraint sets as lists of pairs of types, the constraint generation algorithm is a direct transcription of the inference rules given in the solution to 22.3.9.

   let rec recon ctx nextuvar t = match t with         TmVar(fi,i,_) →           let tyT = getTypeFromContext fi ctx i in           (tyT, nextuvar, [])       | TmAbs(fi, x, tyT1, t2) →           let ctx' = addbinding ctx x (VarBind(tyT1)) in           let (tyT2,nextuvar2,constr2) = recon ctx' nextuvar t2 in           (TyArr(tyT1, tyT2), nextuvar2, constr2)       | TmApp(fi,t1,t2) →           let (tyT1,nextuvar1,constr1) = recon ctx nextuvar t1 in           let (tyT2,nextuvar2,constr2) = recon ctx nextuvar1 t2 in           let NextUVar(tyX,nextuvar') = nextuvar2() in           let newconstr = [(tyT1,TyArr(tyT2,TyId(tyX)))] in           ((TyId(tyX)), nextuvar',            List.concat [newconstr; constr1; constr2])       | TmZero(fi) → (TyNat, nextuvar, [])       | TmSucc(fi,t1) →           let (tyT1,nextuvar1,constr1) = recon ctx nextuvar t1 in           (TyNat, nextuvar1, (tyT1,TyNat)::constr1)       | TmPred(fi,t1) →           let (tyT1,nextuvar1,constr1) = recon ctx nextuvar t1 in           (TyNat, nextuvar1, (tyT1,TyNat)::constr1)       | TmIsZero(fi,t1) →           let (tyT1,nextuvar1,constr1) = recon ctx nextuvar t1 in           (TyBool, nextuvar1, (tyT1,TyNat)::constr1)       | TmTrue(fi) → (TyBool, nextuvar, [])       | TmFalse(fi) → (TyBool, nextuvar, [])       | TmIf(fi,t1,t2,t3) →           let (tyT1,nextuvar1,constr1) = recon ctx nextuvar t1 in           let (tyT2,nextuvar2,constr2) = recon ctx nextuvar1 t2 in           let (tyT3,nextuvar3,constr3) = recon ctx nextuvar2 t3 in           let newconstr = [(tyT1,TyBool); (tyT2,tyT3)] in           (tyT3, nextuvar3,            List.concat [newconstr; constr1; constr2; constr3])

22.3.11 Solution

A constraint generation rule for fix expressions can be derived straightforwardly from the typing rule T-FIX in Figure 11-12.

This rule reconstructs t₁'s type (calling it T₁), makes sure that T₁ has the form X→X for some fresh X, and yields X as the type of fix t₁.

A constraint generation rule for letrec expressions can in turn be derived from this one, together with the definition of letrec as a derived form.

22.4.3 Solution

   {X = Nat, Y = X→X}      [X ↦ Nat, Y ↦ Nat→Nat]   {Nat→Nat = X→Y}            [X ↦ Nat, Y ↦ Nat]   {X→Y = Y→Z, Z = U→W}  [X ↦ U↦W, Y ↦ U↦W, Z ↦ U↦W]   {Nat = Nat→Y}                Not unifiable   {Y = Nat→Y}                    Not unifiable   {}                                      []

22.4.6 Solution

The main data structure needed for this exercise is a representation of substitutions. There are many alternatives; a simple one is to reuse the constr datatype from Exercise 22.3.10: a substitution is just a constraint set, all of whose left-hand sides are unification variables. If we define a function substinty that performs substitution of a type for a single type variable

   let substinty tyX tyT tyS =     let rec f tyS = match tyS with         TyArr(tyS1,tyS2) → TyArr(f tyS1, f tyS2)       | TyNat → TyNat       | TyBool → TyBool       | TyId(s) → if s=tyX then tyT else TyId(s)     in f tyS

then application of a whole substitution to a type can be defined as follows:

   let applysubst constr tyT =     List.fold_left       (fun tyS (TyId(tyX),tyC2) → substinty tyX tyC2 tyS)       tyT (List.rev constr)

The unification function also needs to be able to apply a substitution to all the types in some constraint set:

   let substinconstr tyX tyT constr =     List.map       (fun (tyS1,tyS2) →          (substinty tyX tyT tyS1, substinty tyX tyT tyS2))       constr

Also crucial is the "occur-check" that detects circular dependencies:

   let occursin tyX tyT =     let rec o tyT = match tyT with         TyArr(tyT1,tyT2) → o tyT1 || o tyT2       | TyNat → false       | TyBool → false       | TyId(s) → (s=tyX)     in o tyT

The unification function is now a direct transcription of the pseudocode given in Figure 22-2. As usual, it takes a file position and string as extra arguments to be used in printing error messages when unification fails.

   let unify fi ctx msg constr =     let rec u constr = match constr with         [] → []       | (tyS,TyId(tyX)) :: rest →           if tyS = TyId(tyX) then u rest           else if occursin tyX tyS then             error fi (msg ^ ": circular constraints")           else             List.append (u (substinconstr tyX tyS rest))                         [(TyId(tyX),tyS)]       | (TyId(tyX),tyT) :: rest →           if tyT = TyId(tyX) then u rest           else if occursin tyX tyT then             error fi (msg ^ ": circular constraints")           else             List.append (u (substinconstr tyX tyT rest))                         [(TyId(tyX),tyT)]       | (TyNat,TyNat) :: rest → u rest       | (TyBool,TyBool) :: rest → u rest       | (TyArr(tyS1,tyS2),TyArr(tyT1,tyT2)) :: rest →           u ((tyS1,tyT1) :: (tyS2,tyT2) :: rest)       | (tyS,tyT)::rest →           error fi "Unsolvable constraints"     in       u constr

This pedagogical version of the unifier does not work very hard to print useful error messages. In practice, "explaining" type errors can be one of the hardest parts of engineering a production compiler for a language with type reconstruction. See Wand (1986).

22.5.6 Solution

Extending the type reconstruction algorithm to handle records is not straightforward, though it can be done. The main difficulty is that it is not clear what constraints should be generated for a record projection. A naive first attempt would be

but this is not satisfactory, since this rule says, in effect, that the field l_i can be projected only from a record containing just the field l_i and no others.

An elegant solution was proposed by Wand (1987) and further developed by Wand (1988, 1989b), Remy (1989, 1990), and others. We introduce a new kind of variable, called a row variable, ranging not over types but over "rows" of field labels and associated types. Using row variables, the constraint generation rule for field projection can be written

where σ and ρ are row variables and the operator ⊕ combines two rows (assuming that their fields are disjoint). That is, the term t.l_i has type X if t has a record type with fields ρ, where ρ contains the field l_i:X and some other fields σ.

The constraints generated by this refined algorithm are more complicated than the simple sets of equations between types with unification variables of the original reconstruction algorithm, since the new constraint sets also involve the associative and commutative operator ⊕. A simple form of equational unification is needed to find solutions to such constraint sets.

23.4.3 Solution

Here is the standard solution using an auxiliary append

   append = λX. (fix (λapp:(List X) → (List X) → (List X).                    λl1:List X. λl2:List X.                      if isnil [X] l1 then l2                      else cons [X] (head [X] l1)                                    (app (tail [X] l1) l2))); ▸ append : "X. List X → List X → List X   reverse =     λX.      (fix (λrev:(List X) → (List X).             λl: (List X).              if isnil [X] l              then nil [X]              else append [X] (rev (tail [X] l))                              (cons [X] (head [X] l) (nil [X])))); ▸ reverse : "X. List X → List X

23.4.5 Solution

   and = λb:CBool. λc:CBool.           λX. λt:X. λf:X. b [X] (c [X] t f) f;

23.4.6 Solution

   iszro = λn:CNat. n [Bool] (λb:Bool. false) true;

23.4.8 Solution

   pairNat = λn1:CNat. λn2:CNat.               λX. λf:CNat→CNat→X. f n1 n2;   fstNat = λp:PairNat. p [CNat] (λn1:CNat. λn2:CNat. n1);   sndNat = λp:PairNat. p [CNat] (λn1:CNat. λn2:CNat. n2);

23.4.9 Solution

   zz = pairNat c₀ c₀;   f = λp:PairNat. pairNat (sndNat p) (cplus c₁ (sndNat p));   prd = λm:CNat. fstNat (m [PairNat] f zz);

23.4.10 Solution

   vpred = λn:CNat. λX. λs:X→X.                 λz:X.                   (n [(X→X)→X]                      (λp:(X→X)→X. λq:(X→X). q (p s))                      (λx:X→X. z))                     (λx:X. x); ▸ vpred : CNat → CNat

I'm grateful to Michael Levin for making me aware of this example.

23.4.11 Solution

   head = λX. λdefault:X. λl:List X.             l [X] (λhd:X. λtl:X. hd) default;

23.4.12 Solution

The insertion function is the trickiest part of this exercise. This solution works by applying the given list l to a function that constructs two new lists, one identical to the original and the other including e. For each element hd of l (working from right to left), this function is passed hd and the pair of lists already constructed for the elements to the right of hd. The new pair of lists is built by comparing e with hd: if it is smaller or equal, then it belongs at the beginning of the second resulting list; we therefore build the second resulting list by adding e to the front of the first list we were passed (the one that does not yet contain e). On the other hand, if e is greater than hd, then it belongs somewhere in the middle of the second list, and we construct a new second list by simply appending hd to the already-constructed second list that we were passed.

   insert =     λX. λleq:X→X→Bool. λl:List X. λe:X.       let res =         l [Pair (List X) (List X)]           (λhd:X. λacc: Pair (List X) (List X).              lets rest = fst [List X] [List X] acc in              let newrest = cons [X] hd rest in              let restwithe = snd [List X] [List X] acc in              let newrestwithe =                 if leq e hd                   then cons [X] e (cons [X] hd rest)                   else cons [X] hd restwithe in              pair [List X] [List X] newrest newrestwithe)           (pair [List X] [List X] (nil [X]) (cons [X] e (nil [X])))       in snd [List X] [List X] res; ▸ insert : "X. (X→X→Bool) → List X → X → List X

Next we need a comparison function for numbers. Since we're using primitive numbers, we need to use fix to write it. (We could avoid fix altogether by using CNat here instead of Nat.)

   leqnat =     fix (λf:Nat→Nat→Bool. λm:Nat. λn:Nat.            if iszero m then true            else if iszero n then false            else f (pred m) (pred n)); ▸ leqnat : Nat → Nat → Bool

Finally, we construct a sorting function by inserting each element of the list, in turn, into a new list:

   sort = λX. λleq:X→X→Bool. λl:List X.             l [List X]               (λhd:X. λrest:List X. insert [X] leq rest hd)               (nil [X]); ▸ sort : "X. (X→X→Bool) → List X → List X

To test that sort is working correctly, we construct an out-of-order list,

   l = cons [Nat] 9         (cons [Nat] 2 (cons [Nat] 6 (cons [Nat] 4 (nil [Nat]))));

sort it,

   l = sort [Nat] leqnat l;

and read out the contents:

   nth =     λX. λdefault:X.       fix (λf:(List X)→Nat→X. λl:List X. λn:Nat.              if iszero n                then head [X] default l                else f (tail [X] l) (pred n)); ▸ nth : "X. X → List X → Nat → X   nth [Nat] 0 l 0; ▸ 2 : Nat   nth [Nat] 0 l 1; ▸ 4 : Nat   nth [Nat] 0 l 2; ▸ 6 : Nat   nth [Nat] 0 l 3; ▸ 9 : Nat   nth [Nat] 0 l 4; ▸ 0 : Nat

The demonstration that a well-typed sorting algorithm could be implemented in System F was a tour de force by Reynolds (1985). His algorithm was a little different from the one presented here.

23.5.1 Solution

The structure of the proof is almost exactly the same as for 9.3.9 (see page 107). For the type application rule E-TAPPTABS, we need one additional substitution lemma, paralleling Lemma 9.3.8 (see page 106).

If Г, X, Δ ⊢ t : T, then Г, [X ↦ S]Δ ⊢ [X ↦ S]t : [X ↦ S]T.

The extra context Δ here is needed to obtain a strong enough induction hypothesis; if it is omitted, the T-ABS case will fail.

23.5.2 Solution

Again, the structure of this proof is very similar to the proof of progress for λ_→, Theorem 9.3.5. The canonical forms lemma (9.3.4) is extended with one additional case

If v is a value of type "X.T₁₂, then v = λX.t₁₂.

which is used in the type application case of the main proof.

23.6.3 Solution

All of the parts are relatively straightforward inductive and/or calculational arguments, except the last, where a bit more insight is needed to see how to piece things together and obtain a contradiction. Pawel Urzyczyn suggested the structure of this argument.

Straightforward induction on t, using the inversion lemma for typing.
We show, by induction on the number of outer type abstractions and applications, that
- If t has the form 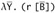for some , , 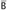and r (where r is not necessarily exposed), and if erase(t) = m and Г ⊢ t : T, then there is some type s of the form 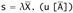, with erase(s) = m and Г ⊢ s : T, where furthermore u is exposed.
In the base case, there are no outer type abstractions or applications—i.e., r itself is exposed and we are finished.

In the induction case, the outer constructor of r is either a type abstraction or a type application. If it is a type application, say r₁ [R], we add R to the sequence 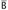and apply the induction hypothesis. If it is a type abstraction, say λZ. r₁, then there are two subcases to consider:
1. If the sequence of applications 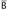is empty, then we can add Z to the sequence of abstractions and apply the induction hypothesis.
2. If 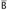is nonempty, then we may write t as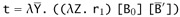
  
  where 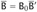. But this term contains an R-BETA2 redex; reducing this redex leaves us with the term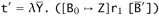
  
  where [B₀ ↦ Z]r₁ contains strictly fewer outer type abstractions and applications than r. Furthermore, the subject reduction theorem tells us that t′ has the same type as t. The desired result now follows by applying the induction hypothesis.
Immediate from the inversion lemma.
Straightforward calculation from parts (1), (3), and (2) [twice].
Immediate from part (2) and the inversion lemma.
By induction on the size of T₁. In the base case, where T₁ is a variable, this variable must come from 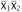, since otherwise we would have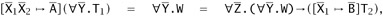

which cannot be the case (there are no arrows on the left and at least one on the right). The other cases follow directly from the induction hypothesis.
Suppose, for a contradiction, that omega is typable. Then, by parts (1) and (3), there is some exposed term ∘ = s u where
- erase(s) = λx. x x
  
  erase(u) = λy. y y
  
  Г ⊢ s : U→V
  
  Г ⊢ u : U.
By part (2), there exist terms 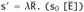and 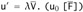with s₀ and u₀ exposed and
- erase(s₀) = λx. x x
  
  erase(u₀) = λy. y y
  
  Г ⊢ s′ : U→V
  
  Г ⊢ u′ : U.
Since s′ has an arrow type, 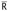must be empty. Similarly, since s₀ and u₀ are exposed, they must both begin with abstractions, so 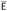and 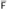are also empty, and we have
- ∘′
  
  =
  
  s′ u′
  
  =
  
  =
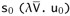
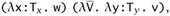
where erase(w) = x x and erase(v) = y y. By the inversion lemma, U = T_x and
- Г, x:T_x ⊢ w : W
  
  Г, 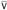, y:T_y ⊢ v : P.
Applying part (4) to the first of these, either
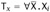1. , or
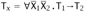2. , and, for some 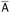and ,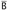
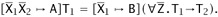
By part (5), T_x must have the second form, so, by part (6), the leftmost leaf of T₁ is .

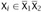Now, applying part (4) to the typing Г, 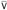, y:T_y ⊢ v : P, we have either
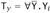1. , or
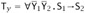2. , and, for some 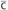and ,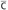
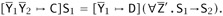
In the former case, we have immediately that the leftmost leaf of T_y is . In the latter case, we can use (6) to see that that, again, the leftmost leaf of T_y is .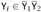

But, from the shape of ∘′ and the inversion lemma, we have

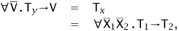
so, in particular, T_y = T₁. In other words, the leftmost leaf of T₁ is the same as that of T_y. In summary, then, we have 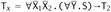, with both 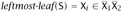and 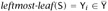. Since the variables 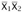and 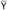are bound at different places, we have derived a contradiction: our original assumption that omega is typable must be false.

23.7.1 Solution

   let r = λX. ref (λx:X. x) in   (r[Nat] := (λx:Nat. succ x);    (!(r[Bool])) true);

24.1.1 Solution

The package p6 provides a constant a and a function f, but the only operation permitted by the types of these components is applying f to a some number of times and then throwing away the result. The package p7 allows us to use f to create values of type X, but we can't do anything with these values. In p8, both components can be used, but now there is nothing hidden—we might as well drop the existential packaging altogether.

24.2.1 Solution

   stackADT =      {*List Nat,       {new = nil [Nat],        push = λn:Nat. λs:List Nat. cons [Nat] n s,        top = λs:List Nat. head [Nat] s,        pop = λs:List Nat. tail [Nat] s,        isempty = isnil [Nat]}}    as {$Stack, {new: Stack, push: Nat→Stack→Stack, top: Stack→Nat,                  pop: Stack→Stack, isempty: Stack→Bool}}; ▸ stackADT : {$Stack,                {new:Stack,push:Nat→Stack→Stack,top:Stack→Nat,                 pop:Stack→Stack,isempty:Stack→Bool}}   let {Stack,stack} = stackADT in   stack.top (stack.push 5 (stack.push 3 stack.new)); ▸ 5 : Nat

24.2.2 Solution

   counterADT =      {*Ref Nat,       {new = λ_:Unit. ref 1,        get = λr:Ref Nat. !r,        inc = λr:Ref Nat. r := succ(!r)}}      as {$Counter,          {new: Unit→Counter, get: Counter→Nat, inc: Counter→Unit}}; ▸ counterADT : {$Counter,                  {new:Unit→Counter,get:Counter→Nat,                   inc:Counter→Unit}}

24.2.3 Solution

   FlipFlop = {$X, {state:X, methods: {read: X→Bool, toggle: X→X,                                       reset: X→X}}};   f = {*Counter,        {state = zeroCounter,         methods = {read = λs:Counter. iseven (sendget s),                    toggle = λs:Counter. sendinc s,                    reset = λs:Counter. zeroCounter}}}       as FlipFlop; ▸ f : FlipFlop

24.2.4 Solution

   c = {*Ref Nat,        {state = ref 5,         methods = {get = λx:Ref Nat. !x,                    inc = λx:Ref Nat. (x := succ(!x); x)}}}       as Counter;

24.2.5 Solution

This type would allow us to implement set objects with union methods, but it would prevent us from using them. To invoke the union method of such an object, we need to pass it two values of the very same representation type X. But these cannot come from two different set objects, since to obtain the two states we would need to open each object, and this would bind two distinct type variables; the state of the second set could not be passed to the union operation of the first. (This is not just stubbornness on the part of the typechecker: it is easy to see that it would be unsound to pass the concrete representation of one set to the union operation of another, since the representation of the second set may in general be arbitrarily different from the first.) So this version of the NatSet type only allows us to take the union of a set with itself!

24.3.2 Solution

At a minimum, we need to show that the typing and computation rules of existentials are preserved by the translation—i.e., that if we write 〚—〛 for the function that performs all of these translations, then Г ⊢ t: T implies 〚Г〛 ⊢ 〚t〛 : 〚T〛 and t →* t′ implies 〚t〛 →* 〚t′〛. These properties are easy to check. We might also hope to find that the converses are true—i.e., that an ill-typed term in the language with existentials is always mapped to an ill-typed term by the translation, and a stuck term to a stuck term; these properties, unfortunately, fail: for example, the translation maps the ill-typed (and stuck) term ({*Nat, 0} as {$X.X}) [Bool] to a well-typed (and not stuck) one.

24.3.3 Solution

I am not aware of any place where this is written out. It seems that it should be possible, but that the transformation will not be local syntactic sugar—it will need to be applied to a whole program all at once.

25.2.1 Solution

The d-place shift of a type T above cutoff c, written , is defined as follows:

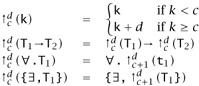
Write for the d-place shift of all the variables in a type T, i.e., ↑^d(T).

25.4.1 Solution

It makes space for the type variable X. The result of substituting v₁₂ into t₂ is supposed to be well-scoped in a context of the form Г, X, whereas the original v₁₂ is defined relative to just Г.

26.2.3 Solution

One place where the full F_<: rule is required is in the object encoding of Abadi, Cardelli, and Viswanathan (1996), also described in Abadi and Cardelli (1996).

26.3.4 Solution

   spluszz = λn:SZero. λm:SZero.                λX. λS<:X. λZ<:X. λs:X→S. λz:Z.                  n [X] [S] [Z] s (m [X] [S] [Z] s z);   spluspn = λn:SPos. λm:SNat.                λX. λS<:X. λZ<:X. λs:X→S. λz:Z.                  n [X] [S] [X] s (m [X] [S] [Z] s z); ▸ spluspn : SPos → SNat → SPos

26.3.5 Solution

   SBool  = "X. "T<:X. "F<:X. T→F→X;   STrue  = "X. "T<:X. "F<:X. T→F→T;   SFalse = "X. "T<:X. "F<:X. T→F→F;   tru = λX. λT<:X. λF<:X. λt:T. λf:F. t; ▸ tru : STrue   fls = λX. λT<:X. λF<:X. λt:T. λf:F. f; ▸ fls : SFalse   notft = λb:SFalse. λX. λT<:X. λF<:X. λt:T. λf:F. b[X][F][T] f t; ▸ notft : SFalse → STrue   nottf = λb:STrue. λX. λT<:X. λF<:X. λt:T.  λf:F. b[X][F][T] f t; ▸ nottf : STrue → SFalse

26.4.3 Solution

In the abstraction and type abstraction cases in parts (1) and (2), and the quantifier case in (3) and (4).

26.4.5 Solution

Part (1) proceeds induction on subtyping derivations. All of the cases are either immediate (S-REFL, S-TOP) or straightforward applications of the induction hypothesis (S-TRANS, S-ARROW, S-ALL) except S-TVAR, which is more interesting. Suppose the final rule of the derivation of Г, X<:Q, Δ ⊢ S <: T is an instance of S-TVAR, i.e., S is some variable Y and T is the upper bound of Y in the context. There are two possibilities to consider. If X and Y are different variables, then the assumption Y<:T can also be found in the context Г, X<:P, Δ, and the result is immediate. On the other hand, if X = Y, then T = Q; to complete the argument, we need to show that Г, X<:P, Δ ⊢ X <: Q. We have by S-TVAR that Г, X<:P, Δ X <: P. Moreover, by assumption, Г, ⊢ P <: Q, so by weakening (Lemma 26.4.2), Г, X<:P, Δ ⊢ P <: Q. Pasting these two new derivations together with S-TRANS yields the desired result.

Part (2) is a routine induction on typing derivations, using part (1) for the subtyping premise of the type application case.

26.4.11 Solution

All the proofs are by straightforward induction on subtyping derivations. We show just the first, proceeding by case analysis on the final rule in the derivation. The cases for S-REFL and S-TOP are immediate. S-TVAR cannot happen (the left-hand side of the conclusion of S-TVAR can only be a variable, not an arrow); similarly, S-ALL cannot happen. If the final rule is an instance of S-ARROW, the subderivations are the desired results. Finally, suppose the last rule is an instance of S-TRANS—i.e., we have Г ⊢ S₁ → S₂ <: U and Г ⊢ U <: T for some U. By the induction hypothesis, either U is Top (in which case T is also Top by part (4) of the exercise and we are done) or else U has the form U₁ → U₂ with Г ⊢ U₁ <: S₁ and Г ⊢ S₂ <: U₂. In the latter case, we apply the induction hypothesis again to the second subderivation of the original S-TRANS to learn that either T = Top (and we are done) or else T has the form T₁ → T₂ with Г ⊢ T₁ <: U₁ and Г ⊢ U₂ <: T₂. Two uses of transitivity tell us that Г ⊢ T₁ <: S₁ and Г ⊢ S₂ <: T₂, from which the desired result follows by S-ARROW.

26.5.1 Solution

26.5.2 Solution

Without subtyping, there are just four:

   {*Nat, {a=5,b=7}} as {$X, {a:Nat,b:Nat}};   {*Nat, {a=5,b=7}} as {$X, {a:X,b:Nat}};   {*Nat, {a=5,b=7}} as {$X, {a:Nat,b:X}};   {*Nat, {a=5,b=7}} as {$X, {a:X,b:X}};

With subtyping and bounded quantification, there are quite a few more—for example:

   {*Nat, {a=5,b=7}} as {$X, {a:Nat}};   {*Nat, {a=5,b=7}} as {$X, {b:X}};   {*Nat, {a=5,b=7}} as {$X, {a:Top,b:X}};   {*Nat, {a=5,b=7}} as {$X, Top};   {*Nat, {a=5,b=7}} as {$X<:Nat, {a:X,b:X}};   {*Nat, {a=5,b=7}} as {$X<:Nat, {a:Top,b:X}};

26.5.3 Solution

One way to accomplish this is to nest the reset counter ADT inside of the counter ADT:

   counterADT =      {*Nat,       {new = 1, get = λi:Nat. i, inc = λi:Nat. succ(i),        rcADT =          {*Nat,           {new = 1, get = λi:Nat. i, inc = λi:Nat. succ(i),            reset = λi:Nat. 1}}          as {$ResetCounter<:Nat,              {new: ResetCounter, get: ResetCounter→Nat,               inc: ResetCounter→ResetCounter,               reset: ResetCounter→ResetCounter}} }}      as {$Counter,          {new: Counter, get: Counter→Nat, inc: Counter→Counter,           rcADT:             {$ResetCounter<:Counter,              {new: ResetCounter, get: ResetCounter→Nat,               inc: ResetCounter→ResetCounter,               reset: ResetCounter→ResetCounter}}}}; ▸ counterADT : {$Counter,                  {new:Counter,get:Counter→Nat,inc:Counter→Counter,                   rcADT:{$ResetCounter<:Counter,                           {new:ResetCounter,get:ResetCounter→Nat,                            inc:ResetCounter→ResetCounter,                            reset:ResetCounter→ResetCounter}}}}

When these packages are opened, the result is that the context in which the remainder of the program is checked will contain type variable bindings of the form Counter<:Top, counter:{...}, ResetCounter<:Counter, resetCounter:{...}:

   let {Counter,counter} = counterADT in   let {ResetCounter,resetCounter} = counter.rcADT in   counter.get     (counter.inc        (resetCounter.reset (resetCounter.inc resetCounter.new))); ▸ 2 : Nat

26.5.4 Solution

All we need to do is to add bounds in the obvious places to the encoding from §24.3. At the level of types, we get:

The changes at the level of terms follow directly from this.

27.1 Solution

Here is one way:

   setCounterClass =     λM<:SetCounter. λR<:CounterRep.     λself: Ref(R→M).       λr: R.          {get = λ_:Unit. !(r.x),           set = λi:Nat.  r.x:=i,           inc = λ_:Unit. (!self r).set (succ((!self r).get unit))}; ▸ setCounterClass : "M<:SetCounter.                       "R<:CounterRep.                        (Ref (R→M)) → R → SetCounter   instrCounterClass =     λM<:InstrCounter.     λR<:InstrCounterRep.     λself: Ref(R→M).       λr: R.         let super = setCounterClass [M] [R] self in            {get = (super r).get,             set = λi:Nat. (r.a:=succ(!(r.a)); (super r).set i),             inc = (super r).inc,             accesses = λ_:Unit. !(r.a)}; ▸ instrCounterClass : "M<:InstrCounter.                         "R<:InstrCounterRep.                          (Ref (R→M)) → R → InstrCounter   newInstrCounter =     let m = ref (λr:InstrCounterRep. error as InstrCounter) in     let m' =       instrCounterClass [InstrCounter] [InstrCounterRep] m in     (m := m';      λ_:Unit. let r = {x=ref 1, a=ref 0} in m' r); ▸ newInstrCounter : Unit → InstrCounter

28.2.3 Solution

In the T-TABS case, we add a trivial use of S-REFL to supply the extra premise for S-ALL. In the T-TAPP case, the subtype inversion lemma (for full F_<:) tells us that N₁ = "X<:N₁₁.N₁₂, with Г ⊢ T₁₁ <: N₁₁ and Г, X<:T₁₁ ⊢ N₁₂ <: T₁₂. Using transitivity, we see that Г ⊢ T₂ <: T₁₁, which justifies using TA-TAPP to obtain . We finish, as before, using the preservation of subtyping under substitution (Lemma 26.4.8) to obtain Г ⊢ [X ↦ T₂]N₁₂ <: [X ↦ T₂]T₁₂ = T.

28.5.1 Solution

Theorem 28.3.5 (in particular, the case for S-ALL) fails for full F_<:.

28.5.6 Solution

Note, first, that bounded and unbounded quantifiers should not be allowed to mix: there should be a subtyping rule for comparing two bounded quantifiers and another for two unbounded quantifiers, but no rule for comparing a bounded to an unbounded quantifier. Otherwise we'd be right back where we started!

For parts (1) and (2), see Katiyar and Sankar (1992) for details. For part (3), the answer is no: adding record types with width subtyping to the restricted system makes it undecidable again. The problem is that the empty record type is a kind of maximal type (among record types), and it can be used to cause divergence in the subtype checker using a modified version of Ghelli's example. If T = "X<:{}. ¬{a: "Y<:X. ¬Y}, then the input X₀<:{a:T} ⊢ X₀ <: {a: "X₁ <:X₀. ¬X₁} will cause the subtype checker to diverge.

Martin Hofmann helped me work out this example. The same observation was made by Katiyar and Sankar (1992).

28.6.3 Solution

I count 9 common subtypes:

   "X<:Y′→Z. Y→Z′      "X<:Y′→Z. Top→Z′      "X<:Y′→Z. X   "X<:Y′→Top. Y→Z′    "X<:Y′→Top. Top→Z′    "X<:Y′→Top. X   "X<:Top. Y→Z′       "X<:Top. Top→Z′       "X<:Top. X.

Both "X<:Y′→Z. Y→Z′ and "X<:Y′→Z. X are lower bounds for S and T, but these two types have no common supertype that is also a subtype of S and T.
Consider S→Top and T→Top. (Or "X<:Y′→Z. Y→Z′ and "X<:Y′→Z. X.)

28.7.1 Solution

The functions R_X,Г and L_X,Г, mapping types to their least X-free supertype and their largest X-free subtype, respectively, are defined in Figure A-2. (To avoid clutter, we elide the subscripts X and Г.) The two definitions have different side-conditions, since, whenever L appears, we have to check whether it is defined (written L(T) ≠ fail), while R is always defined, thanks to the presence of the Top type. The correctness of these definitions is proved in Ghelli and Pierce (1998).

Figure A-2: Minimal X-Free Supertype and Maximal X-Free Subtype of a Given Type

28.7.2 Solution

One easy way to show the undecidability of full bounded existentials (due to Ghelli and Pierce, 1998) is to give a translation 〚—〛 from subtyping problems in full F_<: into subtyping problems in the system with only existentials such that Г ⊢ S <: T is provable in F_<: iff 〚Г ⊢ S <: T〛 is provable in the system with existentials. This encoding can be defined on types by

   〚X〛          =  X                 〚Top〛    =  Top   〚"X<:T₁.T₂〛  =  ¬{$X<:T₁,¬〚T₂〛}    〚T₁→T₂〛  =  〚T₁〛→〚T₂〛

where ¬S = "X<:S.X. We extend it to contexts by 〚X₁<:T₁, ,..., X_n<:T_n〛 = X₁<:〚T₁〛, ..., X_n<:〚T〛, and to subtyping statements by 〚Г ⊢ S <: T〛 = 〚Г〛 ⊢ 〚S〛 <: 〚T〛.

29.1.1 Solution

"X.X→X is a proper type, with elements like λX.λx:X.x. These terms are polymorphic functions that, when instantiated with a type T, yield a function from T to T. By contrast, λX.X→X is a type operator—a function that, when applied to a type T, yields the proper type T→T of functions from T to T.

In other words, "X.X→X is a type whose elements are term-level functions from types to terms; instantiating one of these (by applying it to a type, written t [T]) yields an element of the arrow type T→T. On the other hand, λX.X→X is itself a function (from types to types); instantiating it with a type T (written (λX.X→X) T) yields the type T→T itself, not one of its elements.

For example, if fn has type "X.X→X and Op = λX.X→X, then fn [T] : T→T = Op T.

29.1.2 Solution

Nat→Nat is a (proper) type of functions, not a function at the level of types.

30.3 Solution

Lemma 30.3.1 is used in the T-ABS, T-TAPP, and T-EQ cases. Lemma 30.3.2 is used in the T-VAR case.

30.3.8 Solution

By induction on the total sizes of the given derivations, with a case analysis on the final rules of both. If either derivation ends with QR-REFL, then the other derivation is the desired result. If either derivation ends with QR-ABS, QR-ARROW, or QR-ALL, then by the form of the rules, both derivations must end with the same rule, and the result follows by straightforward use of the induction hypothesis. If both derivations end with QR-APP, then the result again follows by straightforward use of the induction hypothesis. The remaining cases are more interesting.

If both derivations end with QR-APPABS, then we have

S = (λX::K₁₁ .S₁₂) S₂

T = [X ↦ T₂]T₁₂

U = [X ↦ U₂]U₁₂,

with

S₁₂ ⇛ T₁₂

S₂ ⇛ T₂

S₁₂ ⇛ U₁₂

S₂ ⇛ U₂.

By the induction hypothesis, there are V₁₂ and V₂ such that

T₁₂ ⇛ V₁₂

T₂ ⇛ V₂

U₁₂ ⇛ V₁₂

U₂ ⇛ V₂.

Applying Lemma 30.3.7 twice, we obtain [X ↦ T₂]T₁₂ ⇛ [X ↦ V₂]V₁₂ and [X ↦ U₂]U₁₂ ⇛ [X ↦ V₂]V₁₂—that is, T ⇛ V and U ⇛ V.

Finally, suppose one derivation (say, the first one) ends with QR-APP and the other with QR-APPABS. In this case, we have

S = (λX::K₁₁.S₁₂) S₂

U = [X → U₂]U₁₂,

where again S₁₂ ⇛ T₁₂, S₂ ⇛ T₂, S₁₂ ⇛ U₁₂, and S₂ ⇛ U₂. Again, by the induction hypothesis, there are V₁₂ and V₂ such that T₁₂ ⇛ V₁₂, T₂ ⇛ V₂, U₁₂ ⇛ V₁₂, and U₂ ⇛ V₂. Applying rule QR-APPABS to the first and second of these and Lemma 30.3.7 to the third and fourth gives us T ⇛ V and U ⇛ V.

30.3.10 Solution

We first observe that we can reorganize any derivation of so that neither symmetry nor transitivity is used in a subderivation of an instance of the symmetry rule—that is, we can get from S to T by a sequence of steps pasted together with QR-TRANS, where each step consists of a single-step reduction optionally followed by a single instance of symmetry. This sequence can be visualized as follows.

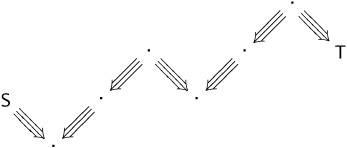
(arrows pointing from right to left are reductions ending with symmetry, while left to right arrows are un-symmetrized reductions). We now use Lemma 30.3.8 repeatedly to add small diamonds to the bottom of this picture until we reach a common reduct of S and T.

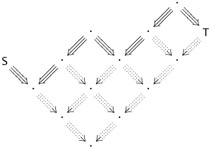
The same argument can also be presented in a standard inductive form, without appealing to pictures, but this will probably just make it harder to understand without making it any more convincing.

30.3.17 Solution

If we add the first weird rule, the progress property will fail; preservation, though, is fine. If we add the second rule, both progress and preservation will fail.

30.3.20 Solution

Compare your solution with the sources for the fomega checker.

30.5.1 Solution

Instead of the type family FloatList n, we now have the parametric type family List T n, with the following operations:

   nil   :  "X. FloatList X 0   cons  :  "X. Πn:Nat. X → FloatList X (succ n)   hd    :  "X. Πn:Nat. List X (succ n) → X   tl    :  "X. Πn:Nat. List X (succ n) → List X n

31.2.1 Solution

   Г  ⊢  A                     <:  Id B                      Yes   Г  ⊢  Id A                  <:  B                         Yes   Г  ⊢  λX.X                  <:  λX.Top                    Yes   Г  ⊢  λX. "Y<:X. Y          <:  λX. "Y<:Top. Y            No   Г  ⊢  λX. "Y<:X. Y          <:  λX. "Y<:X. X              Yes   Г  ⊢  F B                   <:  B                           Yes   Г  ⊢  B                     <:  F B                       No   Г  ⊢  F B                   <:  F B                       Yes   Г  ⊢  "F<:(λY.Top→Y). F A  <:  "F<:(λY.Top→Y). Top→ B  Yes   Г  ⊢  "F<:(λY.Top→Y). F A  <:  "F<:(λY.Top→Y). F B      No   Г  ⊢  Top[*⇒*]             <:  Top[*⇒*⇒*]              No

32.5.1 Solution

The key observation is that Object M is an existential type: Object is an abbreviation for the operator

   λM::*⇒*. {$X, {state:X, methods:M X}}

When we apply this to M we obtain a redex, which reduces to the existential type

   {$X, {state:X, methods:M X}}.

Note that no subsumption—hence no information loss—is involved in this transformation.

32.7.2 Solution

The minimal typing property fails for the calculus the way we have defined it. Consider the term

   {#x={a=5,b=7}}.

This can be given both of the types {#x:{a:Nat}} and {#x:{a:Nat,b:Nat}}, but these types are incomparable. One reasonable fix for this is to explicitly annotate each invariant field in a record term with its intended type. This effectively gives the programmer the responsibility of choosing between the two types above.

32.5.2 Solution

   sendget =     λM<<:CounterM. λo:Object M.       let {X, b} = o in b.methods.get(b.state);   sendreset =     λM<:ResetCounterM. λo:Object M.       let {X, b} = o in         {*X,          {state = b.methods.reset(b.state),           methods = b.methods}}  as Object M;

32.9.1 Solution

   MyCounterM =     λR. {get: R→Nat, set:R→Nat→R, inc:R→R, accesses:R→Nat,              backup:R→R, reset:R→R};   MyCounterR = {#x:Nat,#count:Nat,#old:Nat};   myCounterClass =     λR<:MyCounterR.     λself: Unit→MyCounterM R.     λ_:Unit.        let super = instrCounterClass [R] self unit in        {get = super.get,         set = super.set,         inc = super.inc,         accesses = super.accesses,         reset = λs:R. s→x=s.old,         backup = λs:R. s→old=s.x}    as MyCounterM R; mc = {*MyCounterR,        {state = {#x=0,#count=0,#old=0},         methods = fix (myCounterClass [MyCounterR]) unit}}       as Object MyCounterM; sendget [MyCounterM]   (sendreset [MyCounterM] (sendinc [MyCounterM] mc));

"My dear Watson, try a little analysis yourself," said he, with a touch of impatience. "You know my methods. Apply them, and it will be instructive to compare results." —A. Conan Doyle, The Sign of the Four (1890)

How to put it impeccably may be left as an exercise for the reader. I avail myself here of a favorite ploy by which mathematicians spare themselves sticky patches of exposition. —W. v. O. Quine (1987)

< Free Open Study >

erase(s) = λx. x x	erase(u) = λy. y y
Г ⊢ s : U→V	Г ⊢ u : U.

erase(s₀) = λx. x x	erase(u₀) = λy. y y
Г ⊢ s′ : U→V	Г ⊢ u′ : U.