Risk-Adjusted Financial Management

Overview

Value increases when the satisfaction of the customer augments and the expenditure of resources diminishes.

Robert Tassinari
Le Rapport Qualite/Prix, 1985

In Chapter 1, we discussed the idea of the balanced scorecard as one of the business scoring models driving the selection and funding of projects. On every scorecard there are quantitative financial measures that set the bar for project selection and for project success or failure. It is inescapable that project managers will be involved in financial measures and in the financial success of projects. Financial performance in projects, like every other aspect of project performance, is subject to uncertainty: uncertainty of performance by the project team; uncertainty of performance by vendors, suppliers, and partners; and ultimately, uncertainty of financial performance by project deliverables in the marketplace. Uncertainty, we know, is risk. In this chapter, we introduce the financial concepts most important to the project manager, but we introduce them in the context of risk adjustments that are made to provide a more realistic context for measurement and evaluation.

Financial Statements

Finance officers have long-established standards for reporting the numbers. The general body of knowledge for accounting standards is contained in the Generally Accepted Accounting Principles (GAAP), published and maintained by the accounting industry. Within your business, the controller (comptroller, if you are in the government) is the chief accountant. The controller interprets and applies the GAAP to the specifics of your company.

Financial information is more often than not presented on a set of "financial statements." We will discuss three of those statements that are of most use to the project manager. The statements are:

• The expense statement: Often called the "profit and loss" or "P&L" statement, the expense statement is where project financial expenses are "recognized" by the controller and recorded each period. We will learn that not all expenses on the expense statement are cash expenses, so to keep the books on the expense statement means keeping track of more than just the checks that are written. A common refrain is: "Cash is a fact, but profit is an opinion." [1] This reflects the thought that the expense statement is subject to much interpretation of the GAAP, whereas cash is tangible and well understood without ambiguity.
• The balance sheet: The balance sheet is a two-sided ledger that we studied in Chapter 3. It is a recording of a snapshot in time of the dollar value of all the assets, liabilities, and capital employed on the project.
• The cash flow statement: Actual cash going into or out of the company or project is recorded on the cash flow statement. It is on the cash flow statement that we actually see "sources and uses" of cash in the project.

The neat thing about these statements is that they actually all play together, something engineers and project professionals would call system integration, but accountants would call "balance" or "reconciliation." Even though one statement may measure flow and another may measure a value at a point in time, over the life of the project an entry on any one of these statements has a corresponding response on another statement. Collectively, and with their risk-adjusted partners, net present value and economic value add, the project financial statements provide a rich source of information about the performance of projects.

The chart of accounts was discussed in the chapter on the work breakdown structure (WBS). The chart of accounts is the controller's WBS of the business. The WBS of the project is just an extension of the WBS of the business, i.e., the chart of accounts. In this chapter, we will discuss the "trial balance" as a reporting tool for financial and project managers that is closely tied to the chart of accounts and the financial statements.

The Expense Statement

The expense statement, sometimes known as the income or P&L (profit and loss) statement, is an ordered list of the revenue and expense items for the project. The item categories and ordering of the categories is by account from the chart of accounts. Typically, there are accounts listed and expense entries for labor and labor benefits, purchased materials, travel, training, facility supplies and consumables, information services for data processing, networks and computer environments, vendor charges, facility rent and utilities, freight and fuel, capital depreciation expenses, general and administrative (G&A) expenses, sales and marketing expenses, legal and contract management expenses, taxes, and perhaps others, but not deliverables. It is very unlikely that you will see a project deliverable on the controller's expense statement for the project. The expense statement is therefore a "view" of the expenses from the controller's point of view.

Table 5-1 illustrates a project P&L.

Table 5-1: P&L Statement for Project

Statement Item	$0.00
Revenue from operations (Special note: project deliverables not operational)	$0.00
Direct expenses
Fixed expenses
Rent of project facilities	$2,000.00
Utilities of project facilities	$250.00
Project management staff labor compensation	$80,000.00
Project management staff compensation benefits	$16,000.00
Network and communications chargeback	$350.00
Total fixed expenses	$98,600.00
Variable expenses
Work package labor compensation	$850,000.00
Work package compensation benefits	$170,000.00
Office supplies	$500.00
Work package purchased materials	$45,000.00
Travel and subsistence	$10,000.00
Training for staff	$5,000.00
Rental and operating leases	$3,500.00
Total variable expenses	$1,084,000.00
Total direct expenses	$1,182,600.00
Indirect expenses
Indirect allocation of direct support expenses @ 100% of labor compensation	$930,000.00
G&A expenses (% direct)
Independent R&D @ 2%	$23,652.00
General executive management @ 15%	$177,390.00
Legal, HR, finance, contracts, IT @ 12%	$141,912.00
Selling expenses @ 3%	$35,478.00
Total indirect expenses	$1,308,432.00
Indirect rate (indirect/direct)	111%
Depreciation of capital assets
Special tools and facilities for project	$30,000.00
Software over $25,000	$525.00
Capital leases for special vehicles	$1,200.00
Total depreciation	$31,725.00
Total operating income (expense)	($1,340,157.00)

The Expense Statement and the Work Breakdown Structure

From the discussion in Chapter 2, we know that the project expenses on the WBS are typically presented from a "deliverables point of view" since the mission of the project manager is to provide the deliverables for not more than the resources committed to the project. Therefore, at the project level, the expense statement may have to be "mapped" to the project WBS. For example, there may be an expense item for travel and subsistence on the expense statement provided by the controller. The travel and subsistence within each WBS element should roll up to the figures in the expense statement for the same things, in this case travel and subsistence. If expenses within the project WBS are coded and identified according to the expense statement, it can be a simple matter for the project administrator to extract and add together these elements to "balance" or "reconcile" the expense statement with the WBS. Figure 5-1 shows a simple case of relating the expense statement to the WBS.

Figure 5-1: Expense Statement Mapping to the WBS.

Most large companies run their business accounting on an "accrual basis," rather than on a cash basis. The consequence of the accrual method is that expenses can be reserved or recognized before any cash changes hands. Accrual accounting thus leads us to the fact that not all expenses are actually cash; they may only be an accrual that is being "recognized" in a particular period. For example, taxes are typically accrued each month as a recognized expense on the expense statement, but they are paid each April. The cash flow will be seen on the April cash flow statement even though "expenses" have been seen each period on the expense statement. In April, the cash flow will reconcile or balance with the cumulative expense statement insofar as taxes are concerned. Similarly, benefits, like vacation, are accrued as expenses each period. Sometimes the project manager sets up an accrual for a vendor or subcontractor's expenses so that their expenses are "smoothed" into each period. Then, when the vendor invoice is paid, the cumulative expense statement and the cash flow statements will reconcile and balance. Figure 5-2 shows an example of the process described.

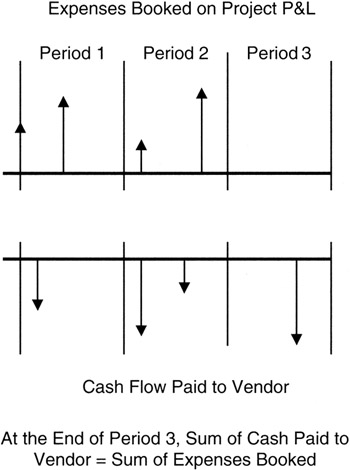
Figure 5-2: Cash Flow and Expense Reconciliation.

The Balance Sheet

In Chapter 3 we discussed the connection between the balance sheet and the expense statement. Expenses are logged on the "T" charts and totals moved to the balance sheet at the next "snapshot in time." The most important aspect of the balance sheet insofar as the project manager is concerned is the "capitalized expense" that is shown on the balance sheet. Large material purchases, and in some cases labor expenses, both internal and supplier provided, as allowed by the GAAP, are often "capitalized." "Capitalized" is a verb that has been coined to capture the idea that certain cash expenses should not be recognized on the expense statement until the item that was purchased is put into use. The GAAP idea is to align use and cost of use in the same accounting period. The balance sheet is where the unrecognized expense is maintained until the time comes to "expense" it to the expense statement. The process of expensing the balance sheet is called "depreciating," and the expense is called "depreciation expense." For example, if a truck is bought for the project in June and depreciation begins in September, when the truck goes into use on the project, there is no actual cash expense in September. The cash went out of the business in June when the truck was purchased. Depreciation is one of the prominent "noncash" expenses on the expense statement. Accruals, already discussed, are the other prominent noncash expenses.

The Balance Sheet and the Work Breakdown Structure

How would the project team handle the truck example: purchase a truck for cash in June and then put the truck into service in September when depreciation begins? Obviously the work package schedule would show the purchase activity in June and the service activity beginning in September. Regarding the financial part of the transaction, a common practice is for the project manager to maintain a capital budget for the capital items, like a truck, that are to be purchased for the project and for the work package manager to maintain an expense budget. (We will discuss some of the special factors in capital budgeting in subsequent paragraphs of this chapter.) The capital budget would have the schedule and record of the cash purchase; the expense budget would begin in September for the truck and show the depreciation expense in the work package. Each period, the balance sheet would be reduced by the amount depreciated onto the expense statement. When depreciation is completed, the sum of the depreciation expenses should equal the initial cash purchase.

The Cash Flow Statement

Now we come to the cash and to the flow of cash. As described by Robert Higgins in his book, Analysis for Financial Management, [2] the cash flow statement is commonly thought of as the place to put down the sources of cash and uses of cash in the project. Viewed this way as a double entry system, the sources ought to balance the uses. Flow refers to a change over time. As such, a cash flow statement is not a statement of cash on hand, but rather the change in cash over the reporting period.

There are only two ways a company can generate cash: decrease an asset or increase a liability. Decreasing the accounts receivable asset account brings cash into the company that is recorded on the P&L as revenue; selling a building or a truck brings cash into a business. Taking cash out of a checking account brings cash into a company. This last example is often confusing. How can reducing the cash balance of a company's checking account be a source of cash for the company? Think of it this way: reducing the balance in the asset account puts cash in the hands of the company's management just as if you had cashed a check on your personal account at a bank. The cash value of the checking account is no more actual cash than the cash value of the truck.

Correspondingly, the only two uses of cash are to increase an asset or decrease a liability. Paying vendors reduces the accounts payable liability account, as does paying off a loan. Adding to the cash balance of a checking account or acquiring a capital asset, like a truck, increases assets and is a use of cash.

Table 5-2 shows an example of a cash flow statement presented as sources and uses. Another form of the cash flow statement arranges the items into three categories: cash from operations; cash from investments in property, plant, and equipment; and cash from financing activities like stock sales. Even so, the sum of the total uses must balance the sum of the total sources.

Table 5-2: Sources and Uses

Sources of Project Cash	$000
Reductions in checking cash	$38.5
Increase notes (debt) from project investor	$5
Increase current accounts payable for project purchases	$4
Increase accrued benefits on project staff	$35
TOTAL sources of CASH	$82.5

Uses of Project Cash	$000
Increase short-term notes to project supplier	$15
Increase prepaid licenses	$10
Increase capital assets for project	$20
Reductions in accrued labor for staff	$37.5
TOTAL uses of CASH	$82.5

Unfortunately, there is no single definition of cash or cash flow, but there are several in common use, some of which will be important to project managers:

• Net cash flow is defined as "net income from the expense statement plus or minus noncash adjustments." [3]
• Net cash flow from operations is defined as net cash flow plus or minus the changes in current liabilities and assets.
• Free cash flow is defined as the cash available to distribute to shareholders or owners.
• Discounted cash flow is taken to be the present value of net cash flow or net cash flow from operations.

For projects, we will be concerned with the present value of the net cash flow from operations for net present value calculations and net cash flow for economic value add calculations.

The Cash Flow Statement and the Work Breakdown Structure

The WBS is not usually reconciled directly with the cash flow statement. Ordinarily the project manager manages the capital budget, whereas the WBS reflects the expense budget. The project manager's practice may be to reconcile the capital budget with the WBS work packages for the reporting period. However, if the project WBS is on a cash-accounting basis, then the WBS provides the sources and uses of cash in the project.

The Trial Balance for Project Managers

The controller will undoubtedly provide a "trial balance" to the project manager each month. The trial balance is a report of debits and credits by account, typically summed for each account so that at report time a specific account will show a net value in the debit column or a net value in the credit column, but not in both columns at once. Recall that there is no such thing as a "negative debit" because a "negative debit" is recorded as a positive credit. The debit or the credit amount is a report of the value of the account on the report date. The trial balance follows the same protocol as the balance sheet: asset accounts are debited to increase their value and credited to decrease their value; just the opposite is done for liability and capital accounts.

Naturally, the debits and credits of the trial balance should balance. The project manager is often called on to reconcile and correct the account values shown on the trial balance. Table 5-3 illustrates an example.

Table 5-3: Trial Balance for Project

Expense Account	Equity Account	Capital Account	Debit	Credit
Prepaid expenses			$500,000
Accrued compensation				$250,000
Travel and subsistence			$300,000
Checking			$300,000
Communications			$50,000
Rent and utilities			$550,000
	Paid in stock			$1,000,000
	Long-term debt			$250,000
		Accumulated depreciation Capital equipment		$200,000
			$300,000
	Total debits and credits		$1,700,000	$1,700,000

The Trial Balance and the Work Breakdown Structure

Everything on the WBS must roll up to some account on the chart of accounts. Assuming that the project administrator has a mapping of the WBS accounts to the chart of accounts, the WBS can be reconciled to the trial balance using pivot queries in a spreadsheet.

[1]Pike, Tom, Retool, Rethink, Results, Simon & Schuster, New York, 1999.

[2]Higgins, Robert C., Analysis for Financial Management, Irwin McGraw-Hill, Boston, MA, 1998, chap. 1, pp. 16–21.

[3]Higgins, Robert C., Analysis for Financial Management, Irwin McGraw-Hill, Boston, MA, 1998, chap. 1, p. 19.

Capital Budgeting

Capital budgeting is about how to budget and spend cash for the big-ticket items on the project. Spending cash creates cash flow. The cash flow statement is one of the important tracking tools for the capital budget. Capital budgeting is closely related to the concept of discounted cash flow (DCF), a methodology to assign risk (that is, a discount) to cash flows that will occur in the future. In this section we address the capital budgeting per se and address its close cousin, DCF, in the next section.

Capital Budgeting for Projects

Capital budgets refer to those project budgets for which cash is paid out now, in the present during the project execution, but for which the expense will be recognized in the future when the item is put into use. The principle at work is "alignment": use and the cost of use should align in the same period. Expensing could begin during project execution if the capital purchase is to be used for the project itself, or expensing could be deferred until the capital item is to be used for operations after project completion. Expensing the capital item "relieves" the balance sheet amount for the item each time an expense is recorded on the expense statement. When the balance sheet amount is fully relieved (that is, the amount on the balance sheet is $0), then expensing ends. Table 5-4 provides an example. The controller will make the decision about what project items to make capital purchases and when the expensing of those items will begin.

Table 5-4: Expensing the Balance Sheet

Item	Year 0	Year 1	Year 2	Year 3	Year 4
Balance sheet capital employed, crane with truck	$500,000	$375,000	$250,000	$125,000	$0
Depreciation to the P&L statement, straight line method*	$0	$125,000 = $500,000/4	$125,000 = $500,000/4	$125,000 = $500,000/4	$125,000 $500,000/4
Balance sheet capital employed, software license	$500,000	$300,000	$150,000	$50,000	$0
Depreciation to the P&L statement, sum of years method (4 + 3 + 2 + 1 = 10) [*]	$0	$200,000 = (4/10) * $500,000	$150,000 = (3/10) * $500,000	$100,000 = (2/10) * $500,000	$50,000 = (1/10) * $500,000
[*]Notes: In the straight line method, an equal amount is expensed to the P&L each period, In the sum of years method, the number of years is added cumulatively to find the denominator; the numerator is the "year number."

So far, our discussion has been about paying cash for a capital item. It is possible to lease a capital item and thereby create a "capital lease." A capital lease shows up on the balance sheet as a liability, just like a purchased item would show as an asset. The lease payments are expensed, thereby relieving the balance sheet liability. There are several tests the controller applies to determine if a lease is a capital lease or an "operating lease." The latter is expensed just like a rental item or an item bought on credit. The controller is the ultimate decision maker on whether a lease is a capital lease or an operating lease.

Capital Structure and Projects

Going back to the discussion of the balance sheet in Chapter 3, we know that assets on the left side are "paid for" or "financed" by liabilities on the right side. Owners, shareholders, debt holders, and suppliers are the creditors of the business. The relative weight of debt and owner capital paid in is called the "capital structure" of the company. Generally speaking, the long-term debt (like capital leases, notes and bonds, and capital paid in for stock or partnership) finances the long-term capital purchases; short-term debt (such as accounts payable to suppliers) finances the short-term assets (like accounts receivables).

For project managers, the importance of the capital structure is this: there is a "cost of capital" that is passed along to the project. For the most part, the cost of capital is not a real expense that shows up on an expense statement, but it is an "opportunity cost" that creates competition for capital. If the project loses out in the capital competition, the project is starved of the resources it needs or the project is never approved in the first place.

Opportunity Cost for Projects

The opportunity cost works as follows for projects: If a company has investment dollars that can be made available to projects, which projects should get what amounts? The decision is usually made on the basis of benefit returns to the company. The ratios in play are the ROI (return on investment), the net present value (NPV), and the economic value add (EVA). We will define these for the project manager and demonstrate their application to projects in subsequent paragraphs.

Suffice it to say, benefit returns are risky because they are earned in the future. Therefore, benefit returns must be risk adjusted before they are plugged into the formula. The opportunity cost is then the difference in returns, after risk adjustment, between one project opportunity and the next most favorable opportunity that is competing for the same capital.

The role of project managers in the capital competition is twofold: provide risk management so that the returns are maximized to the extent possible, and manage capital budgets to minimize capital expenditures. Those two activities will maximize the returns and minimize the opportunity cost of the project.

Consider an example project situation as shown in Table 5-5. There we see two projects, each with different demands on capital and expense, but each with an equal face-value opportunity for net benefits, $175,000. If not for considering the confidence of obtaining the returns, there is no opportunity cost between these two projects. However, our confidence in one project's return is higher than the other. On a risk-adjusted basis, there is a "cost" of selecting the more risky project. The cost we speak of is an opportunity cost of picking one over the other. To ensure the selection of the more favorable project, the decision policy must embrace the concept of opportunity cost. The objective of the project team is to make the risk factors as favorable as possible in order to create the greatest competitive advantage for the project.

Table 5-5: Opportunity Cost for Projects

Project Manager's Responsibility			Project Sponsor's Responsibility
Capital Employed	Expenses	Confidence in Capital and Expense	Benefits Over Three Years	Confidence in Benefits	Net Risk Adjusted Return
Project A
$350,000 (depreciate over three years)	$125,000 (one year)	80%	$650,000 cumulative	75%	Compared to B higher cost risk, same benefit risk
Project B
$50,000	$300,000	90%	$525,000	75%	Compared to A lower cost risk, same benefit risk
Project A Benefit - Cost = $650 - $475 = $175 Project B Benefit - Cost = $525 - $350 = $175
Opportunity Cost A = Project A - Project B higher risk Opportunity Cost B = -Project A + Project B lower risk
Without considering risk, the opportunity cost of Project A vs. Project B is $0.

Discounted Cash Flow

The concept of DCF for projects often governs whether or not a project will be selected to go forward, or whether or not a change in scope requiring new resources will be approved. Those are two good reasons why project managers should be familiar with the concept. The controller's office usually makes the DCF calculations for the project manager. However, the project manager often influences the risk factors that go into determining the discount rate. Thus, the project manager is not entirely a passive partner in the DCF deliberations.

The Discount Rate

The discount rate, sometimes called an interest rate, but also called the cost of capital rate or factor, is the discount applied to future cash flows to account for the risk that those flows may not happen as planned or to create "equivalence" with another investment opportunity. [4] Discounting gives us a present-time feel for the value of future flows, having taken risk and alternate opportunities into account.

Many things can be considered in determining the discount rate: real interest that could be earned on an alternate opportunity, the risk of inflation, the risk that the market will not be accepting of the project deliverables, the risk that customers will not have the capacity to pay in the future because of some mishap in the economy, the risk that the project will not be completed on time in order to exploit a market opportunity, or that the project will consume more capital than planned.

It is not uncommon for different discount rates to be applied to different projects in the same company because of the different risk factors faced by each project. Ordinarily, to make discounting practical, all projects of similar type are given the same discount factor, such as all pharmaceutical projects discounted at one rate and all real estate projects discounted at another rate.

Net Present Value and Net Future Value

You may recognize that discounting is the inverse of the familiar idea of compounding. Compounding begins with a present value and forecasts a future value based on an interest rate or capital factor rate. Discounting begins with a forecasted future value to which a discount factor is applied to obtain a present value of the amount. In the same project, the compounding factor and the discount rate are the same rate. Therefore, it is relatively easy to work from the present to the future or from the future back to the present.

Most of us who have had a savings or investment account are familiar with the compounding formula, so let's begin with compounding as a lead-in to discounting. Let's use "k" as the compounding (or discounting factor) and compute the values at the end of the compounding period:

Future value (FV) = Present value (PV) * (1 + k)N

where N is the number of periods to be compounded. N takes on values from N = 0 to some value "m".

To take a simple numerical example, if "k" = 8% and "N" = 3, then we can calculate the future value:

FV = PV * (1 + 0.08)3

FV = PV * 1.2597

Thus, if we had an opportunity to invest $10,000 for three years, we have an expectation that $12,597 will be returned to us at the end of three years, given that the compounding factor is 8%. The return on our investment is the net of the investment and the total return: $12,597 - $10,000 = $2,597.

If we had other opportunities to evaluate, the opportunity costs would be the difference in returns between each opportunity. The factor 1.2597 is called the future value factor. Future value factors are distinguished by always being a number equal to or larger than 1. Future value factors are easily calculated in Excel using the "power" function or they can be found in future value tables in finance books. Table 5-6 is an abridged collection of future value factors.

Table 5-6: Future Value Factors

Discount Rate	Year 0	Year 1	Year 2	Year 3	Year 4
5%	1	1.05	1.1025	1.157625	1.215506
7%	1	1.07	1.1449	1.225043	1.310796
9%	1	1.09	1.1881	1.295029	1.411582
These factors are easily calculated using a spreadsheet. The formula in any particular cell is: Factor = (1 + discount rate)N where N is the number of the year, 0 to 4.
In Excel, the "power" function can be used to calculate the Factor equation. There are two arguments in "power": the first is (1 + discount rate), and the second is N.

Now, about discounting: discounting begins in the future with forecasted flows; the DCF factor "k" is used to find the present value. We solve for present value using the future value formula given above:

PV = FV/(1 + k)N

where N is the number of periods to be compounded.

The present value factors are the inverse of the future value factors. For instance, for m = 3, the present value factor using 8% is 1/1.2597, or 0.7938. All present value factors will be numbers less than or equal to 1. Table 5-7 is an abridged example of present values.

Table 5-7: Present Value Factors

Discount Rate	Year 0	Year 1	Year 2	Year 3	Year 4
5%	1	0.952381	0.907029	0.863838	0.822702
7%	1	0.934579	0.873439	0.816298	0.762895
9%	1	0.917431	0.84168	0.772183	0.708425
These factors are easily calculated using a spreadsheet. The formula in any particular cell is: Factor = 1/(1 + discount rate)N where N is the number of the year, 0 to 4.
In Excel, the "power" function can be used to calculate the denominator in the Factor equation. There are two arguments in "power": the first is (1 + discount rate), and the second is N.

Using the 8% factors and m = 3, suppose we had a forecast for future flows due to a present investment of $10,000 as follows:

N = 0, $10,000 present-time investment outflow

and future forecasted inflows:

N = 1, $3,000, k = 1.08, 1/k = 0.9259

N = 2, $6,000, k2 = 1.082, 1/k2 = 0.8573

N = 3, $7,000, k3 = 1.083, 1/k3 = 0.7938

The present value of these flows given a discount of 8% is given by:

PV(inflows) = $3,000 * 0.9259 + $6,000 * 0.8573 + $7,000 * 0.7938 = $13,478

NPV of return = -$10,000 + $13,478 = $3,478 at the end of three periods.

Figure 5-3 provides a graphical presentation of the cash flows. It is usually simpler to calculate the NPV directly by entering all "outflows" as negative numbers and all "inflows" as positive numbers. In the figure, outflows are arrows pointing down and the inflows are arrows pointing up. With this convention, the above would be written as:

NPV = PV (all inflows) - PV (all outflows)

NPV = PV (all inflows - all outflows)

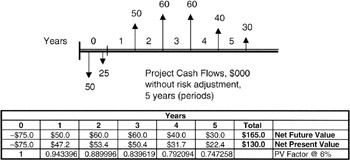
Figure 5-3: NPV Example.

At 8% discount rate:

NPV	=	-$10,000 + $3,000 * 0.9259 + $6,000 * 0.8573 + $7,000 * 0.7938
	=	$3,478

NPV is our first risk-adjusted measure of project financial performance. If the outflows are the cash expended on the project and the inflows are the cash received because of the project, then in the case illustrated above it makes sense to do the project because the NPV ≥ $0. If the NPV is negative, then more money is going out of the business than is coming into the business on a risk-adjusted basis; it makes no financial sense to do projects of negative NPV:

Decision policy: Only projects with NPV ≥ $0 will be selected for execution.

Internal Rate of Return

Now what about this question: Given that the future flows are forecasted, as they were in the example we have just studied, what is the discount factor that makes the NPV exactly $0? We are interested in that factor, which we will call the IRR (internal rate of return), because any discount factor that might be imposed by the controller that is higher than the IRR would cause the NPV to be negative and the project would not be approved.

IRR = Discount rate for which NPV = 0

We cannot solve for the IRR directly. The IRR can only be solved iteratively. For instance, for the project just discussed, using the present value factor tables, we find that at a discount of 24%, the NPV is slightly negative. At 23%, the NPV is slightly positive, meaning the IRR is between 23 and 24%. IRR can be solved in Excel using the IRR function that solves iterative equations. The exact solution is 23.598%.

In some companies, the IRR is called the "hurdle rate." No project can be approved with a discount above the hurdle rate. The IRR is the upper bound of the discount factor for a positive NPV.

Decision policy: The project is acceptable if k < IRR.

When k = IRR, the project is usually not accepted.

Benefit Cost Ratio

The benefit/cost ratio (BCR) is a figure of merit that is often used to evaluate projects. Project managers may be asked to participate in calculating the BCR by evaluating the risks in the project that affect cash flows. The BCR is defined as:

BCR = (PV of all cash inflows)/(PV of all cash outflows)

Defined as above, if BCR > 1, then the project has greater inflow than outflow, the NPV will be positive, and, all other things being equal, the project should be on a list of good candidates:

Decision policy: The project is acceptable if BCR > 1.

Break Even Point

Using the DCFs, the break-even point is when the cumulative project DCFs go from cash negative to cash positive. In equation form, the break-even point occurs when:

Σ PV of discounted cash outflows = Σ PV of discounted cash inflows

Economic Value Add

EVA is a risk-adjusted quantitative measure of project performance. Unlike the previous measures, EVA is focused on earnings. [5] The idea of EVA is that a project should earn more in profits than the cost of the project's capital employed. Remember that capital employed is the liability or equity (resources "owned" by creditors and owners) that finances the expenses of the project. If the project were less profitable than the cost paid for its capital employed, then the creditors and owners would do better to employ their capital elsewhere. Such a competitive rationale should be a component of any rational decision policy.

When working with EVA we use the same risk factors and notation as already developed. The cost of capital factor (CCF) is the discount rate, "k":

The cost of capital employed ($CCE) = k * $Capital employed

Thus, if a project absorbs $100,000 in capital for a year, and the risk factor, CCF, is 8%, then the CCE is $8,000. The project's earnings must exceed $8,000 or else more is being spent on capital than is being earned on the same capital. A special note: the time frame for comparison of earnings and CCE should be identical or else each is subject to different risks. It is common practice to discount all figures to present time for a common comparison.

The first step in looking at EVA is to get a handle on earnings. Earnings are profits and they are portrayed on the P&L. Typically, the P&L would show:

(Revenues - Cash expenses - Noncash expenses) * (1 - Tax rate) = Earnings after tax (EAT)

Immediately we see that noncash expenses save real cash outlays on taxes by subtracting from taxable revenue. For our purposes, we will assume the noncash expense is depreciation of capital assets and that the revenue is from the deliverables of the project. [8]

If we then sum up the EAT for each period and compare the summed EAT to the CCE, we have the EVA for the project.

EVA = EAT - k * CCE

To put EVA in a project context, consider Table 5-8. We assume a $500,000 capital investment in the project and a five-year straight-line depreciation of $100,000 per year. [9] Our capital investment on the balance sheet is relieved ("relieved" is accounting terminology for "reduced") by a depreciation expense each year; each year the capital employed in the project goes down accordingly, and the CCE is less each year as well. Each year we multiply the investment balance on the balance sheet by the cost of capital factor, k, to calculate the cost of capital for that year. Discounting by 1/(1 + k)N each year provides the present value of the cost of capital employed (PV CCE).

Table 5-8: Depreciation in EVA Example

Present	1	2	3	4	5	Total
$0.00	$100,000.00	$100,000.00	$100,000.00	$100,000.00	$100,000.00	$500,000.00	Depreciation
$500,000.00	$400,000.00	$300,000.00	$200,000.00	$100,000.00	$0.00		Capital employed
	0.08	0.08	0.08	0.08	0.08		Discount rate, "k"
	$40,000.00	$32,000.00	$24,000.00	$16,000.00	$8,000.00	$120,000.00	CCE
	$37,037.04	$27,434.84	$19,051.97	$11,760.48	$5,444.67	$100,729.00	PV of CCE
Present = Period 0. Capital employed = nondepreciated value of asset remaining. PV ot CCE = present value of the cost of capital employed.

Now in Table 5-9 we calculate the EVA. For purposes of this example, let's assume the project business case proposes an earnings figure, before noncash additions, of $50,000 per year. That $50,000 is the earnings figure before any risk adjustments. To find the EVA, we simply make the risk adjustments by finding the present value of the EAT and subtracting the PV CCE, and that provides the PV EVA.

Table 5-9: EVA of Project

Present	1	2	3	4	5	Total
	$50,000	$50,000	$50,000	$50,000	$50,000	$250,000	Business case EAT
	$46,296.30	$42,866.94	$39,691.61	$36,751.49	$34,029.16	$199,635.50	PV of EAT
$0.00	$37,037.04	$27,434.84	$19,051.97	$11,760.48	$5,444.67	$100,729.00	PV of CCE
	$9,259.26	$15,432.10	$20,639.64	$24,991.01	$28,584.49	$98,906.50	PV of EVA
	0.08	0.08	0.08	0.08	0.08		Discount rate, "k"
PV of EAT = present value of earnings after tax. PV of CCE = present value of the cost of capital employed. PV of EVA = present value of economic value add.

We see in this example that the EVA is comfortably positive, so this project earns more than it costs to employ the capital.

Economic Value Add and Net Present Value Equivalence

Fortunately for project managers, NPV and EVA are exactly equivalent. NPV is computationally much more straightforward, so EVA-NPV equivalence is a very big convenience indeed. Let's see how this equivalence works in the example project. Table 5-10 shows the calculations.

Table 5-10: EVA-NPV of Project

Present	1	2	3	4	5	Total
EVA of Project
	$50,000.00	$50,000.00	$50,000.00	$50,000.00	$50,000.00	$250,000.00	Business case EAT
	$46,296.30	$42,866.94	$39,691.61	$36,751.49	$34,029.16	$199,635.50	PV of EAT
$0.00	$37,037.04	$27,434.84	$19,051.97	$11,760.48	$5,444.67	$100,729.00	PV of CCE
	$9,259.26	$15,432.10	$20,639.64	$24,991.01	$28,584.49	$98,906.50	PV of EVA
	0.08	0.08	0.08	0.08	0.08		Discount rate, "k"
PV of EAT = present value of earnings after tax. PV of CCE = present value of the cost of capital employed. PV of EVA = present value of economic value add.

NPV of Project
	$50,000.00	$50,000.00	$50,000.00	$50,000.00	$50,000.00	$250,000.00	Business case EAT
$0.00	$100,000.00	$100,000.00	$100,000.00	$100,000.00	$100,000.00	$500,000.00	Depreciation
	$150,000.00	$150,000.00	$150,000.00	$150,000.00	$150,000.00		NCF
	0.08	0.08	0.08	0.08	0.08		Discount rate, "k"
	$138,888.88	$128,600.82	$119,074.84	$110,254.48	$102,087.48	$598,906.50	PV of NCF
						-$500,000.00	PV of investment
						$98,906.50	NPV
PV of NCF = present value of net cash flow.

First, we must reorient ourselves to cash flow rather than earnings. Tom Pike's ditty — "Cash is a fact but profit is an opinion" — jumps to mind. To show equivalence between NPV and EVA, we must find the cash flow from cash earnings. Remember that we define cash earnings as net cash flow (NCF). Also recall the definition previously given of net cash flow: the after-tax earnings with the noncash expenses on the expense statement added back in:

NCF = EAT + Noncash expense

NCF = EAT + Depreciation

From this point the calculations are straightforward: add the EAT and the depreciation together to obtain NCF, calculate NCF present value, and the result is the present value of the cash inflows from earnings. Then subtract the present value of the outflows. The result is the NPV. We see that, to the penny, the EVA and the NPV are the same, though the calculations for NPV are usually much simpler since cash is much easier to measure and track than EAT.

NPV (NCF from operations) = EVA (EAT)

[4]Higgins, Robert C., Analysis for Financial Management, Irwin McGraw-Hill, Boston, MA, 1998, chap. 1, p. 238.

[5]P.T. Finegan first wrote about EVA in the publication Corporate Cashflow. [6] Shawn Tully [7] made EVA popular in a Fortune magazine article after Finegan wrote about EVA.

[5]Finegan, P.T., Financial incentives resolve the shareholder-value puzzle, Corporate Cashflow, pp. 27–32, October 1989.

[5]Tully, S., The real key to creating wealth, Fortune, pp. 38–50, September 1993.

[8]If the project does not generate revenue, but generates cost savings instead, the cost savings can be plugged in since they also create increased earnings.

[9]Depreciation is not always uniformly the same figure each year. There are "accelerated" depreciation methods that take more expense in the early years and less in the later years. The controller will make the decision about which depreciation formula to follow.

Summary of Important Points

Table 5-11 provides the highlights of this chapter.

Table 5-11: Summary of Important Points

Point of Discussion	Summary of Ideas Presented
Financial statements	The general body of knowledge for accounting standards is contained in the Generally Accepted Accounting Principles. Four statements for project managers are: the P&L expense statement, the cash flow statement, the balance sheet, and the trial balance.
P&L statement	The expense statement, sometimes known as the income or P&L statement, is an ordered list of the revenue and expense items for the project. Expenses within the project WBS are coded and identified according to the expense statement.
Balance sheet	The balance sheet is where the unrecognized expense is maintained until the time comes to "expense" it to the expense statement.
Cash flow statement	The cash flow statement is commonly thought of as the place to put down the sources of cash and uses of cash in the project. There are only two ways a company generates cash: (1) decrease an asset or (2) increase a liability.
Discounted cash flow	DCF is taken to be the present value of net cash flow or net cash flow from operations. The discount rate, sometimes called an interest rate, but also called the cost of capital rate or factor, is the discount applied to future cash flows to account for the risk that those flows may not happen as planned. IRR = discount rate for which NPV = 0.
Trial balance	The trial balance is a report of debits and credits by account.
Capital budgeting	Capital budgeting is about how to budget and spend cash for the big-ticket items on the project. Capital budgets refer to those project budgets for which cash is paid out now, in the present during the project execution, but for which the expense will be recognized in the future when the item is put into use.
Opportunity cost	The opportunity cost of the difference in returns, after risk adjust ment, between one project opportunity and the next most favorable opportunity that is competing for the same capital.
Net present value	Present value (PV) = Future value/(1 + k)N. NPV = PV (all inflows) - PV (all outflows). Decision policy: Only projects with NPV ≥ $0 will be selected for execution.
Economic value add	EVA is a risk-adjusted quantitative measure of project performance. A project should earn more in profits than the cost of the project's capital employed. EVA = EAT - k * CCE. NPV (net cash flow from operations) = EVA (after-tax earnings).

References

1. Pike, Tom, Retool, Rethink, Results, Simon & Schuster, New York, 1999.

2. Higgins, Robert C., Analysis for Financial Management, Irwin McGraw-Hill, Boston, MA, 1998, chap. 1, pp. 16–21.

3. Higgins, Robert C., Analysis for Financial Management, Irwin McGraw-Hill, Boston, MA, 1998, chap. 1, p. 19.

4. Higgins, Robert C., Analysis for Financial Management, Irwin McGraw-Hill, Boston, MA, 1998, chap. 1, p. 238.

5. Finegan, P.T., Financial incentives resolve the shareholder-value puzzle, Corporate Cashflow, pp. 27–32, October 1989.

6. Tully, S., The real key to creating wealth, Fortune, pp. 38–50, September 1993.