Cryptography: Theory and Practice:Classical Cryptography | Modern Cryptography: Theory and Practice

Cryptography: Theory and Practice
by Douglas Stinson
CRC Press, CRC Press LLC
ISBN: 0849385210 Pub Date: 03/17/95

Table of Contents

A real matrix K has an inverse if and only if its determinant is non-zero. However, it is important to remember that we are working over 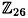. The relevant result for our purposes is that a matrix K has an inverse modulo 26 if and only if gcd (det K, 26) = 1.

We briefly sketch the proof of this fact. First suppose that gcd(det K, 26) = 1. Then det K has an inverse in 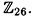Now, for ≤ i ≤ m, 1 ≤ j ≤ m, define K_ij to be the matrix obtained from K by deleting the ith row and the jth column. Define a matrix K* to have as its (i, j)-entry the value (-1)^i+j det K_ji. (K* is called the adjoint matrix of K.) Then it can be shown that

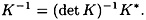
Hence, K is invertible.

Conversely, suppose K has an inverse, K^-1. By the multiplication rule for determinants, we have

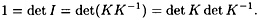
Hence, det K is invertible in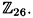

REMARK The above formula for K^-1 is not very efficient computationally, except for small values of m (say m = 2, 3). For larger m, the preferred method of computing inverse matrices would involve elementary row operations.

In the 2 × 2 case, we have the following formula:

THEOREM 1.3

Suppose A = (a_i,j) is a 2 × 2 matrix over 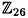such that det A = a_1,1a_2,2 - a_1,2a_2,1 is invertible. Then

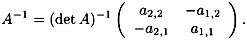
Let’s look again at the example considered earlier. First, we have

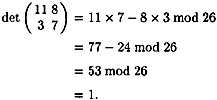
Now, 1^-1 mod 26 = 1, so the inverse matrix is

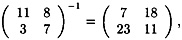
as we verified earlier.

We now give a precise description of the Hill Cipher over 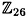in Figure 1.6.

1.1.6 The Permutation Cipher

All of the cryptosystems we have discussed so far involve substitution: plaintext characters are replaced by different ciphertext characters. The idea of a permutation cipher is to keep the plaintext characters unchanged, but to alter their positions by rearranging them. The Permutation Cipher (also known as the Transposition Cipher) has been in use for hundreds of years. In fact, the distinction between the Permutation Cipher and the Substitution Cipher was pointed out as early as 1563 by Giovanni Porta. A formal definition is given in Figure 1.7.

As with the Substitution Cipher, it is more convenient to use alphabetic characters as opposed to residues modulo 26, since there are no algebraic operations being performed in encryption or decryption.

Here is an example to illustrate:

Figure 1.6 Hill Cipher

Figure 1.7 Permutation Cipher

Example 1.6

Suppose m = 6 and the key is the following permutation π:

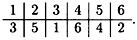
Then the inverse permutation π^-1 is the following:

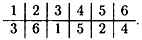
Now, suppose we are given the plaintext

                       shesellsseashellsbytheseashore.

We first group the plaintext into groups of six letters:

                  shesel | lsseas | hellsb | ythese | ashore

Now each group of six letters is rearranged according to the permutation π, yielding the following:

                  EESLSH | SALSES | LSHBLE | HSYEET | HRAEOS

So, the ciphertext is:

                        EESLSHSALSESLSHBLEHSYEETHRAEOS.

The ciphertext can be decrypted in a similar fashion, using the inverse permutation π^-1.

In fact, the Permutation Cipher is a special case of the Hill Cipher. Given a permutation of π of the set {1, . . . , m}, we can define an associated m × m permutation matrix K_π = (k_i,j) according to the formula

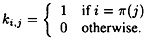
(A permutation matrix is a matrix in which every row and column contains exactly one “1,” and all other values are “0.” A permutation matrix can be obtained from an identity matrix by permuting rows or columns.)

It is not difficult to see that Hill encryption using the matrix K_π is, in fact, equivalent to permutation encryption using the permutation π. Moreover, 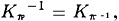, i.e., the inverse matrix to K_π is the permutation matrix defined by the permutation π^-1. Thus, Hill decryption is equivalent to permutation decryption.

For the permutation π used in the example above, the associated permutation matrices are

and

The reader can verify that the product of these two matrices is the identity.

1.1.7 Stream Ciphers

In the cryptosystems we have studied to this point, successive plaintext elements are encrypted using the same key, K. That is, the ciphertext string y is obtained as follows:

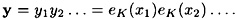
Cryptosystems of this type are often called block ciphers.

An alternative approach is to use what are called stream ciphers. The basic idea is to generate a keystream z = z₁z₂ . . . , and use it to encrypt a plaintext string x = x₁x₂ . . . according to the rule

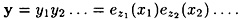
A stream cipher operates as follows. Suppose 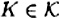is the key and x₁x₂ . . . is the plaintext string. The function f_i is used to generate z_i (the ith element of the keystream), where f_i is a function of the key, K, and the first i - 1 plaintext characters:

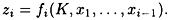
The keystream element z_i is used to encrypt x_i, yielding 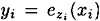. So, to encrypt the plaintext string x₁x₂, . . . , we would successively compute

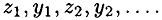
Decrypting the ciphertext string y₁y₂ . . . can be accomplished by successively computing

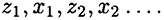
Here is a formal mathematical definition:

Table of Contents