5.3 The Old World of DNA Computing

5.3 The Old World of DNA Computing

The rich diversity of computational models for DNA shows that nucleic acids are extraordinary flexible media for storing and manipulating information. Perhaps this should come as no surprise in that DNA has been used to store and manipulate information for more than 3 billion years. Adleman has helped to open our eyes to the computational riches that have lain hidden all around us for millennia. This has provoked some researchers to look for computation in the natural dynamics in the interior of cells. It has provoked others to try to engineer those dynamics into cells so as to implement human-crafted cellular computers.

Natural Computation in a Cell

Laura Landweber and Lila Kari have led the effort to identify and understand computational processes in natural organisms, though they are certainly not the only ones who have considered life as the processing of information (e.g., G nti 1987; Kampis and Cs nyi 1991; Dawkins 1995). They have focused on gene scrambling in ciliates and the more general phenomenon of RNA editing (Landweber and Kari 2000; Kari and Landweber 2000).

There are more than eight thousand species of ciliates (a form of unicellular eukaryote). Genes in species of the Osytricha genus are often broken into many fragments and coded in the genome in permuted order. For example, the gene encoding DNA polymerase α in O. trifallax seems to be a scrambled sequence of at least 50 sequences. The process of unscrambling closely resembles Adleman's method of generating paths through his graph (1994). The process of constructing the unscrambled genes involves massive copying of the genome along with annealing and recombination to splice together necessary pieces. Each fragment of a gene ends with a sequence that complements the start of the next fragment in the correctly unscrambled gene; however, there are false matches of these sequences to incorrect positions in a genome. These false matches would likely prevent the construction of an unscrambled gene if the process of annealing were random in these ciliates. Apparently, evolution has developed mechanisms for solving this Hamiltonian path problem, but the details of this have yet to be illuminated (Landweber and Kari 2000). Landweber and Kari (2000), however, have developed a formal description of this process and have shown that it is computationally complete.

RNA editing is found in many eukaryotes, including both protozoa and humans. After a sequence of DNA is transcribed into RNA, the sequence or RNA can undergo significant alterations before it is translated into a sequence of amino acids. These editing operations include insertions, deletions, and substitutions. Such editing operations have already been shown to have the power of a universal Turing Machine (Kari 1996; Beaver 1996). This process is apparently carried out by small "guide RNA" (gRNA) molecules that anneal to the target sequence and catalyze an editing operation. In some cases, the results of one editing operation can trigger the next in a cascade somewhat reminiscent of Khodor and Gifford's programmed mutagenesis (2000). In the case of Trypanosoma brucei (a parasite that causes African sleeping sickness), RNA editing creates more than 90 percent of the codons that are translated into amino acids (Landweber and Kari 2000). This technique allows a single sequence in the genome to code for a combinatorial set of amino acid sequences.

Finally, it is interesting to note that information in the cell can be maintained in media beyond just the sequences of nucleic acids in the DNA or RNA. The heritable silencing of genes near the telomeres, which produce mosaic colorings like those of the calico cat, are another form of information storage (Lustig 1998). Unfortunately, we do not yet understand this dynamic enough to harness it for our computing needs.

Artificial Computation in a Cell

There is only a small conceptual jump between recognizing the computational properties of a cell and attempting to harness them (Smith 1995; Knight and Sussman 1997; Eng 2000; Ji 2000; Gardner, Cantor, and Collins 2000; Elowitz and Leibler 2000). There are many desirable properties of cells for the endeavors of DNA computation. Smith (1995) argues that polymerization takes place at least an order of magnitude faster in cells than in vitro. Also, sequences that would be impractically long for in vitro manipulation due to hydrolysis or mechanical shear are protected in the cell by the supercoiling of the DNA.

Knight and Sussman (1997) view the cell as a nice homeostatic environment with its own built-in power source. Their goal is to engineer logic gates into the dynamics of a cell (in this case, E. coli). Although in silicon we encode a low voltage as a 0 and a high voltage as a 1, Knight and Sussman have chosen to encode high and low concentrations of gene products as 1 and 0, respectively. Their first step in this en deavor is the construction of an inverter. All inverters have the general property that when the input is low, the output is high, and vice versa. A good quality inverter has a wide range of low inputs that will make its output high and a wide range of high inputs that will make its output low, with a steep transition between these states, as depicted in figure 5.14. The wide ranges give us a margin for noise and allow the output to be more pure than the input.

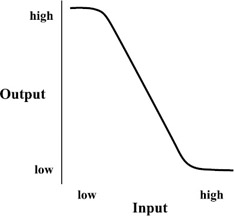
Figure 5.14: The function describing an idealized inverter's mapping of input values to output values. Note that a wide range of low input values maps to a narrow range of high output values. This allows a digital circuit to incrementally remove noise from the system.

An inverter can be implemented by a constitutive gene with a repressor site. A constitutive gene is a gene that is always active in the absence of a repressor. In addition, to make the gene produce a predictable amount of product, we can add negative feedback by making that gene product a repressor of the gene. Knight and Sussman (1997) explored the dynamics of such a system through simulation. Their simulation included the processes of repressor binding and disassociation for two different repressors (the input and the negative feedback of the output), translation of the gene, and gene product degradations. They found that the desired sigmoidal response of the inverter was surprisingly robust to changes in parameters. They have gone on to simulate a closed circuit of three inverters that should produce oscillations in the gene product concentrations (Knight and Sussman 1997). Elowitz and Leibler (2000) scooped them by not only simulating a three-inverter oscillator, but by actually constructing one in E. coli. One surprising result was that the period of oscillations was longer than the period of cell division. This shows that E. coli can maintain their state across cell divisions. Similarly, Gardner and coworkers (Gardner, Cantor, and Collins 2000) constructed a flip-flop (bistable state toggle switch) in E. coli by inserting two genes whose products mutually repress each other. The repression of either product may be inhibited by external signals so as to change the state of the cell.

Eng (2000) takes a more familiar approach by describing an algorithm for solving 3CNF-SAT (or just 3SAT) in a cell. Let the truth and falsehood of a literal be encoded by the presence of one of two distinct gene products (e.g., gene product x_i and gene product x_i). Then create the sequence <reverse of gene x_i> <promotor> <gene x_i>, where the <promotor> sequence is invertible. On the one hand, if the promoter is in the state where transcription is initiated from right to left, gene product x_i will be produced, making the x_i literal true. On the other hand, if the promoter is in the state where transcription is initiated from left to right, gene product x_i will be produced, making the x_i literal false. Note that these states are mutually exclusive. Catalyzing the inversion of the promoter changes the truth value of the literal.

Alternatively, one might use the flip-flop of Gardner and coworkers (Gardner, Cantor, and Collins 2000). A disjunction clause of n variables can be represented by a single unique gene with n alternative promoters, one for each literal gene product. A conjunction can be implemented in a variety of ways: through multiple repressor sites (although the maximum number of repressor sites for any one gene is probably fairly small); through a cascade of reactions, each step requiring one of the input gene products, eventually producing an output product; and finally, we might encode the truth of a disjunction clause as the absence of a gene product. In this last case, a disjunction can be implemented by a constitutive (always on) gene with repressor literals. If any disjunction clause is false, it will produce a promoter protein to turn on the gene for the conjunction. If we make this final conjunction gene code for some reporter protein that is easily observed, then we can observe the truth of the encoded Boolean formula given the state of the literals. The entire process begins by randomly inverting the promoters for the literal genes in a large population of transgenic E. coli carrying our carefully constructed DNA encoding of the formula. Assuming that host cells can tolerate 1Mbase of foreign DNA and it takes 1Kbase per gene with 2n + m + 1 genes (for n literals and m disjunction), we could conceivably solve formulas with 2n + m + 1 = 1000. One liter of solution can hold about 10¹² cells, and thus we might be able to handle up to n = 40 literals (we may have to reset the literals a time or two to generate a truth assignment that satisfies the formula). Of course, in reality both m and n would probably have to be less than 10 due to difficulties in designing the control of the computation. We also have to worry about interfering with the survival of the E. coli when we introduce hundreds of gene products to the cells (Eng 2000). Selection will likely excise the foreign DNA unless it is made necessary to the survival of the cells.