5.2 The New World of DNA Computing

5.2 The New World of DNA Computing

Adleman (1994) demonstrated one particular type of algorithm in DNA called "generate and test". To do this, he had to utilize a handful of techniques from molecular biology, including the construction of sequences of DNA, their hybridization, ligation, polymerase chain reaction, sequence separation, and gel electrophoresis (each of which is described below). But there are many other tools for manipulating DNA and these can be used to implement algorithms beyond the simple brute force approach of generate and test. Which tools and algorithms will turn out to be best for DNA computing is still an open question.

Tools of the Trade

Researchers in DNA computation have plundered molecular biology for tools with which to manipulate and analyze DNA. Luckily, both natural and artificial resources in this new world are abundant. Over the last few billion years, Nature has invented a vast diversity of molecules designed to interact with DNA. Furthermore, the last few decades have witnessed dramatic advances in the technology of molecular biology. There are probably many natural manipulations of DNA that have yet to be discovered. Similarly, there are probably many enzymes and other tools that are known to biologists but have yet to be applied to the endeavor of DNA computation. What follows is a description of those tools and techniques that have been discussed within, and in some cases applied to, DNA computation.

Anneal. This is probably the most basic operation used in DNA computing. Singlestranded complementary DNA will spontaneously form a double strand of DNA when suspended in solution. This occurs through the hydrogen bonds that arise when complementary base pairs are brought into proximity. This is also called "hybridization".

Melt. The inverse of annealing is "melting". That is, the separation of doublestranded DNA (dsDNA) into single-stranded DNA (ssDNA). As the name implies, this can be done by raising the temperature beyond the point where the longest double strands of DNA are stable. Because the hydrogen bonds between the strands are significantly weaker than the covalent bonds between adjacent nucleotides, heating separates the two strands without breaking apart any of the sequences of nucleotides. "Melting" is a bit of a misnomer because the same effect can be achieved by washing the double-stranded DNA in doubly distilled water. The low salt content also destabilizes the hydrogen bonds between the strands of DNA and thereby separates the two strands. Heating to an intermediate temperature can be selectively used to melt apart short double-stranded sequences while leaving longer double-stranded sequences intact.

Ligate. Often invoked after an annealing operation, ligation concatenates strands of DNA. Although it is possible to use some ligase enzymes to concatenate freefloating double-stranded DNA, it is dramatically more efficient to allow single strands to anneal together, connecting up a series of single-strand fragments, and then use ligase to seal the covalent bonds between adjacent fragments, as in figure 5.1.

Polymerase extension. Polymerase enzymes attach to the 3′ end^[3] of a short strand that is annealed to a longer strand. It then extends the 3′ side of the shorter strand so as to build the complementary sequence to the longer strand. This is shown in figure 5.2.

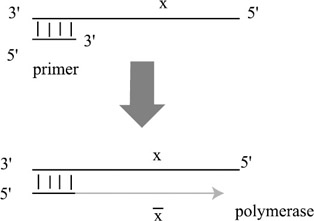
Figure 5.2: Polymerase extension. A polymerase enzyme attaches to the 3′ end of a short primer sequence and constructs the complement (x) of the longer sequence.

Cut. Restriction enzymes will cut a strand of DNA at a specific subsequence. As of 1993, there were over 2,300 different known restriction enzymes that were specific to more than 200 different subsequences. These subsequences are usually on the order of 4–8 nucleotides. Some restriction enzymes will only cleave single-stranded DNA, while others will only cleave double-stranded DNA. Similarly, methylation of the cytosine nucleotides on a strand of DNA interferes with the activity of some restriction enzymes, but not others. Furthermore, some restriction enzymes will cleave a wide range of subsequences of DNA. That is, the specificity of an enzyme relative to its target sequence varies across different enzymes.

Destroy. Subsets of strands can be systematically destroyed, or "digested" by enzymes that preferentially break apart nucleotides in either singleor doublestranded DNA.

Merge. Given two test tubes, combine them, usually by pouring one into the other.

Separate by length. Given a test tube of DNA, split it into two test tubes, one with strands of a particular length, and the other with all the rest. This is done with gel electrophoresis and requires the DNA to be extracted from the gel once the strands of different length have been identified by some form of straining or radioactive tagging.

Reverse chirality. DNA naturally forms two different sorts of double helixes. The most common form has a right-handed chirality and is called B-DNA; however, complementary strands of DNA can also twist around each other in the opposite direction, with left-handed chirality, called Z-DNA. The propensity with which a double strand of DNA forms Z-DNA depends on both the sequences of nucleotides in the strand as well as modifications to those bases (methylation of cytosine's 5 position increases this propensity). Enzymes called topoisomerases can reverse the chirality of a molecule (Seeman et al. 1998).

These basic manipulations can be combined into higher level manipulations. Perhaps the most famous example of a higher level manipulation is polymerase chain reaction (PCR). Composite manipulations include:

Amplify. Given a test tube of DNA, make multiple copies of a subset of the strands present. This is done with polymerase chain reaction (PCR). PCR requires a beginning and an ending subsequence, called "primers", which are usually about twenty base pairs long, to identify the sequence (called the "template") to be replicated. Copies of these subsequences anneal to the single strands, and polymerase enzymes build the complementary strands, as in figure 5.3. Heat then melts apart the double strands, reducing them to single strands and the process repeats, doubling the number of strands in the test tube each cycle.

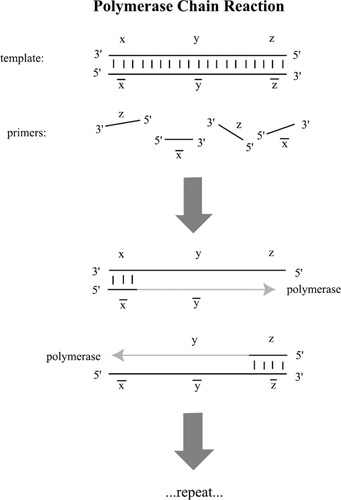
Figure 5.3: Polymerase chain reaction (PCR) follows in cycles of three steps. (1) The double-stranded templates are melted apart. (2) The primers anneal to both strands. (3) A polymerase enzyme extends the primers into replicas of the templates. This is repeated, causing an exponential growth in the number of templates, as long as there are enough primers in the solution to catalyse the reaction. Note that because polymerase attaches to the 3′ end of a primer we need to use the subsequences x and z to get the desired reaction.

Separate by subsequence. Given a test tube of DNA, split it into two test tubes, one with the sequences that contain the specified subsequence, and the other with the rest. We have already seen how this can be done with magnetic beads and the WatsonCrick complement of the specified subsequence, as in Adleman (1994). This is also sometimes called an "extraction". It can also be implemented by destroying the unwanted strands.

Append. This adds a specific subsequence to the ends of all the strands. This can be done by annealing a short strand to a longer strand so that the short strand extends off the end of the longer strand. Then the complement of the subsequence that is extending off the end can be added to the longer strand either through the use of a polymerase enzyme, or through the introduction and annealing of that sequence, cemented by ligase, as depicted in figure 5.1.

Mark. This operation tags strands so that they can be separated or otherwise operated upon selectively. Marking is commonly implemented by making a single strand into a double strand through annealing or the action of a polymerase. It can also mean appending a tag sequence to the end of a strand or even the methylation of the DNA or (de)phosphorylation of the 5′ ends of the strands.

Unmark. The complement of the marking operation. Unmark removes the marks on the strands.

Models of Computation

Now that we know some of the basic operations that can be performed on strands of DNA, we have the pressing question of how those operations should be combined to carry out computations. The question of whether or not DNA is capable of universal computation is no longer at issue. A variety of models have been shown to be computationally complete (Beaver 1995; Boneh, Dunworth, and Sgall 1995; Rothemund 1996; Winfree 1996; Csuhaj-Varj et al. 1996). Of course, we would like the computation to be relatively fast (with few operations that require human intervention), error free (or at least error tolerant), and massively parallel. These are the parameters upon which a proposed model of DNA computation must be measured. Ideally, we would like a "one-pot" computation, such that the computation would play out in a single test tube with a minimum number of external manipulations. Although many models have been invented, none have yet proven themselves practical.

Kazic (2000) suggests that trying to force DNA to emulate our traditional notions of computation may be misguided. Chemical reactions are continuous, they can take on an infinite number of states through a stochastic process, and the reactions do not halt. Kazic argues that this makes modern computational theory inadequate to describe molecular computation. On the other hand, much the same could be said for the electrical medium of conventional computing. Computer engineers have developed ways to channel the continuous real world into the discrete world of digital computation (Knight and Sussman 1997).

It is not yet clear whether we will be forced to abandon attempts to make DNA emulate discrete computations, but that has not stopped many people from trying. There are two general classes of computational models for using DNA. "Generate and test" models are based on Adleman (1994) and Lipton (1995). Alternatives to this brute force approach rely on controlling a sequence of chain reactions to construct a solution to a problem.

Generate and Test

The most popular model for using DNA to do computation comes directly out of Adleman's first paper and falls into the category of "generate and test" algorithms (Adleman 1994, 1996; Boneh, Dunworth, and Sgall 1995; Roweis et al. 1998). The technique was refined into a process with two phases (Boneh, Dunworth, and Sgall 1995; Adleman 1996). First, randomly generate all possible solutions to the problem at hand. Second, isolate the correct solution through repeated separations of the DNA into incorrect solutions and potentially good solutions. At the end of this series of separation steps, it may only be necessary to detect if there are any DNA strands left in the set of good solutions. Adleman's step 5 provides one example.

Generating solutions and then isolating the correct one was easily generalized to finding all the inputs of a Boolean circuit that would result in a specified output (Boneh, Dunworth, and Sgall 1995). Lipton (1995) showed how to generate the set of all^[4] binary strings of length n in O(1), as long as n < 64. Lipton's procedure involves first creating a graph of size O(n) such that a path through the graph is a realization of a binary number of length n. (figure 5.4.) The graph is implemented in the same way as Adleman's (1994). In Lipton's words:

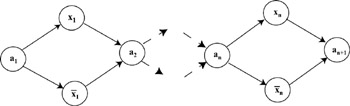
Figure 5.4: Lipton's graph for constructing binary numbers. The vertices and edges are constructed using Adleman's algorithm so that the longest path through the graph will represent an n-bit binary number. If the path goes through an x then it has a 0 at that position, otherwise it has a 1 at that position.

The graph G_n has nodes a₁, x₁, x₁, a₂, …, a_k with edges from a₁ to both x_k and x_k and from both x_k and x_k to a_{k + 1} … : The graph is constructed so that all paths that start at a¹ and end at a_{n + 1} encode an n-bit number. At each stage a path has exactly two choices: If it takes the vertex with an unprimed label, it will encode a 1; if it takes the vertex with a primed label, it will encode a 0. Therefore, the path [a¹ x₁ a₂x₂a₃] encodes the binary number 01.^[5]

The second phase of solving a Boolean circuit involves repeated separations, with a little molecular bookkeeping to keep track of the progress. The idea is to create an ordering on the gates of the circuit so that the inputs of gate g_i are either inputs to the circuit or outputs of gates g_j where j < i. Then, using this ordering, we evaluate the output for the gates, one at a time, given the input values represented in each strand. We append to each strand a bit indicating the value of the output of each gate. This is done in parallel across all the strands, representing all the possible input values. For example, if we are processing gate g_i, then we separate all strands whose inputs to gate g_i would result in the output 1. To these strands we append a subsequence representing 1 with a tag identifying it as the output of gate g_i. To all the other strands we append a 0, and then we merge the two sets in order to process the next gate. Selection is done by using magnetic beads attached to the Watson-Crick complement of the subsequences representing the input bit values. This process is simply repeated until the output gate has been processed. Then all strings with a 1 on the end represent input values that make the circuit output a 1.

Ouyang and coworkers (Ouyang et al. 1997) trumped this with an experimental demonstration of a solution to the maximal clique problem. This is another NPcomplete graph problem. In this case, the problem is to find the largest subset of nodes of the graph in which every node of the subset (clique) is connected to every other node of the subset, as shown in figure 5.5. Their approach was novel in two ways. First they used "parallel overlap assembly" to generate the potential solutions. Second, they used restriction enzymes to digest and thus remove strands that did not represent cliques. A potential solution was coded as a string of value (v_i) and position ( p_i) sequences, one pair for each node (i) in the graph. The value sequences (v_is) could either be 0 (represented by the empty string, or 0 nucleotides) or 1 (represented by a 10-mer sequence). The position sequences (p_is) were represented by unique 20mer sequences. Parallel overlap assembly is similar to Adleman's annealing step in his procedure, except where his adjacent sequences were fused with ligase. Parallel overlap assembly allows larger gaps between adjacent subsequences to be filled in with polymerase, as depicted in figure 5.6. Strands that do not represent cliques can be removed by digesting strands that include pairs of nodes that are not connected by an edge in the graph. This removal is done once for each missing edge in the graph. At the end of this process, PCR was used to amplify the solutions and then gel electrophoresis revealed the shortest remaining sequence that represented the largest clique in the graph.

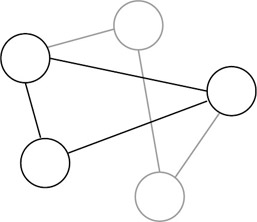
Figure 5.5: An example of a 5-node graph with a 3-node clique shown in black.

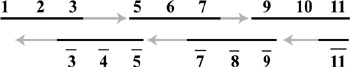
Figure 5.6: Full sequences can be constructed through the combination of short sequences that anneal together and polymerase to fill in the gaps. The grey arrows indicate the activity of polymerase while the numbers and their complements serve to label the sub-sequences. The black lines indicate the input sequences for the process of parallel overlap assembly. PCR will rapidly amplify the fully constructed sequences.

An alternative implementation of bit strings allows for the modification of bits. The "sticker model" (Roweis et al. 1998; Adleman et al. 1996) represents a 0 as a sequence of single-stranded DNA and a 1 as a sequence of double-stranded DNA. The basic structure is a single fixed-length strand representing a string of 0s. Each M-mer interval (where M is about 20 or 30) is unique and encodes a bit position. Thus, to set a bit in all the strands in a test tube, one merely has to add to the test tube a large quantity of the subsequence representing the complement of that bit position. These anneal to the ssDNA and set the bit to 1. A collection of random bit strings can be created by repeatedly splitting the test tube into two test tubes, setting the next bit position in one of the two tubes, and then merging the results. The problem of clearing a single bit position without clearing all the bit positions has not yet been solved and remains a limitation of the sticker model at present.

Adleman (1994) and Lipton (1995) suggested using random encodings to represent information in DNA. But a number of authors have recognized that this can cause problems due to the inadvertent creation of sequences that complement and thus may anneal with each other or themselves (Smith 1995; Deaton et al. 1996; Baum 1998; Hartemink, Gifford, and Khodor 2000). Hartemink and coworkers (Hartemink, Gifford, and Khodor 2000) developed a program SCAN to search for sequences with desired properties to be used for DNA computation. These properties include binding specificity of subsequences to particular locations on a strand, the lack of secondary structure or the formation of dimers (i.e., the sequences should not bind to themselves or others), and different degrees of binding stability in different parts of the strand. The sequences suggested by SCAN proved significantly better than sequences designed by hand (Hartemink, Gifford, and Khodor 2000). Cukras and coworkers (Cukras et al. 2000) solved the knight's problem from chess using RNA rather than DNA.^[6] The knight's problem is the question of how many knights can be fit on a chessboard such that no knight can attack another knight in a single move. They first generated all possible 3 by 3 chessboards with knights as strands of RNA. They then destroyed all illegal boards by annealing other RNA strands to the offending positions and using RNase H to cut the double-stranded RNA. In a sample of 44 remaining strands, 43 were legal board configurations and one encoded the maximal (5) solution (Faulhammer et al. 2000).

Liu and coworkers (Liu et al. 2000b) chose to sacrifice some parallelism for ease of manipulation and reduced error rates by binding ssDNA to a gold surface. They "marked" the strands by annealing sequences to them to form dsDNA and then destroyed unwanted ssDNA with an enzyme that selectively digests ssDNA. They used these operations to demonstrate the solution to the 3SAT problem with four variables and four clauses. They first generated all possible Boolean assignments for the four variables as ssDNA attached to the surface. For each clause, they marked the strands that would satisfy the clause and then destroyed the others. Any strands that remained at the end of this process were sequenced by removing them from the surface, tagging them with a fluorescent dye, and annealing them to complementary strands on a surface whose positions and sequences are known. This requires that all possible strands be laid down in specified positions on the final surface. The labor in constructing such an addressable surface may be offset by the possibility of its repeated use. They do not give an algorithm for determining which strands would satisfy a clause. If this has to be done in silicon, there is no clear advantage of solving 3SAT in DNA. At present, the experiment of Liu and coworkers (Liu et al. 2000b) shows that DNA computation can be done on a surface. They have not shown that this is a promising direction for developing truly useful DNA computations.

Smith (1995) raises the important objection that the naive brute force algorithms of generate-and-test methods can never outperform a good algorithm in silicon for the same problem. For example, Lipton (1995) estimates that his technique for solving 3SAT has an upper bound of 70 literals, yet current computers can already solve 2SAT problems with 300 literals (Smith 1995). Bach and coworkers (Bach et al. 1996: 290–299) recognized the importance of a good algorithm and developed an algorithm of the 3-coloring problem^[7] that only required the generation of Ω(1:89 ⁿ) potential solutions as compared to the brute force algorithm's Ω(3 ⁿ) space requirements. This remains an important area of open problems. Can we improve the efficiency of DNA algorithms to the point where they can compete with silicon computation?

Programmed Chain Reactions

A fundamentally different approach to DNA computation is not to generate and test all possible solutions but rather to control a cascade of chain reactions that results in the answer to a desired computation. If these cascades can be adequately controlled, the parallelism of DNA computation could be utilized for the solution of a vast number of problems (or subproblems) in parallel. A number of computational models of chain reactions in DNA have begun to be experimentally investigated.

Guarnieri and coworkers (Guarnieri, Fliss, and Bancroft 1996) have developed a procedure to implement the addition of two nonnegative binary numbers through a chain reaction. Furthermore, they have demonstrated the algorithm on pairs of single-bit binary numbers. They implement an addition through a cascade of branches in the chain reaction, which are predicated on the value of the sum in the previous bit position. I have summarized their algorithm in pseudo-C code below:

 Int number1[n]; / *Binary numbers represented as arrays of bits. */ Int number2[n]; Carry = 0; /*Keeps track of the carryover from the previous bit. */ N2=0; /* An intermediary variable to hold carry + number2.*/ For (i= 0; i < n; i++){ If (number2[i] ==0)/*Calculate number2 + carry.*/      if (carry==0)           n2= 0;      else n2 = 1;      else      if (carry == 0)           n2= 1;      else n2= 2; if (number1[i] == 0) /*Calculate number1 + n2.*/      switch (n2) {           case 0: output(0); carry = 0; break;           case 1: output(1); carry = 0; break;           case 2: output(1); carry = 1; break;      }      else      switch (n2)           case 0: output(1); carry = 0; break;           case 1: output(0); carry = 1; break;           case 2: output(1); carry = 1; break;      } } if (carry == 1) output(1);/*Spit out any carryover.*/ 

Notice that there is no explicit addition operation in the above algorithm, besides my encoding of the iteration. The branching statements are implemented as annealing operations between the number being constructed (the sum of the two input numbers) and a set of possible complements. Once the number being built (the sum) anneals to the appropriate strand, a polymerase enzyme extends the sum. Then the two strands are melted apart and then cooled so that the sum is free to anneal to the next bit position in the sequence. Each value in each bit position has a unique sequence. Then, if the number2 had a 1 in the 2³ position, there would be two strands added to the soup: one representing the code if (carry == 0) n2= 1 and one representing if (carry == 1) n2 = 2. Then, if the sum had a string at its 3′ end, representing the complement carry == 1 in the 2² position, it would bind to the second option and polymerase would add on the string representing n2=2 at the 2³position.

The same process follows for the reaction with the 2³ position in number1, but this time, three strings would be present in the test tube representing how to extend the sum under each of the three cases n2= 0,1,2. In this way, the addition operation is actually built into the encoding of the two binary numbers. At the end of the chain reaction, the resulting sum must be sequenced in order to determine the result. The addition of 11 + 11 (3 + 3 in binary) is depicted in figures. 5.7, 5.8, and 5.9. The amount of DNA necessary to implement an n-bit addition is only O(n), although it requires the construction of seven unique subsequences (and their complements) for each bit position.

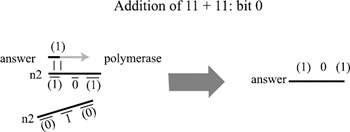
Figure 5.7: Addition proceeds from least significant to most significant bit. The numbers in parentheses represent subsequences encoding partial sums at each bit position. The numbers without parentheses are the bits of the answer. The sub-sequences are all assumed to include patterns that label the bit position, so that (0) at bit position 0 is a different sequence than (0) at bit position 1. Multiple fragments represent the operands n1 and n2. The addition for bit position 0 is simpler than addition for the other positions because there is no carry bit from a previous computation. Thus at the start, the least significant bit of the "answer" is the same as the least significant bit of n1. This bit is then added to the least significant bit of n2 and the result includes both the least significant bit of the sum of n1 and n2 as well as a pattern representing the presence (or absence) of a carry-over bit. Here there are two options for n2, corresponding to the cases where the least significant bit is either (0) or (1). By introducing (1) to the solution, we create an answer sequence (1) 0 (1), indicating that the least significant bit of the answer is 0 and there is a carry-over bit (1).

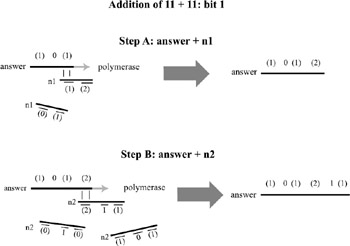
Figure 5.8: For all bit positions other than the least significant bit, addition has to follow in two steps. In step A, the carry-over bit is added to the bit of n1. Then, in step B, the result is added to the bit of n2. Note again that n1 and n2 are both represented as a set of DNA fragments, only one of which will bind to the answer strand in the chain reaction. The 3′ ends of these fragments have been altered to prevent the polymerase extending them.

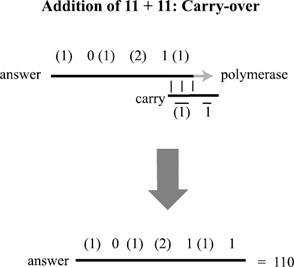
Figure 5.9: Finally, a strand representing the carry-over bit anneals to the answer and completes the process of constructing the answer: 110 (in reverse order), or 6, encoded in binary.

Guarnieri and coworkers (Guarnieri, Fliss, and Bancroft 1996) point out the worst flaw in this algorithm. The encoding of the output number is different from the encoding of the two input numbers. Thus the output cannot be fed back into the DNA computer for future computation without translating it back into the input format. There are further limitations. As they state from the beginning, this procedure only works for nonnegative numbers. Theoretically, this algorithm should be able to handle different addition operations being carried out in parallel as long as all subsequences representing different bit position branches in the test tube are unique and unlikely to bind to each other. Although it is a "one-pot" computation,^[8] it must be driven by temperature cycling. The speed of the cycling is limited in turn by the speed of the annealing reaction and the melting apart of the strands. Because the strand representing the sum may well anneal back again to the last strand that allowed the polymerase to extend the sum, we are not guaranteed that the addition operation will make progress in every temperature cycle. In fact, the strand that will allow progress has fewer base pairs that complement the sum than the last strand that matched it.

Winfree (Winfree 1996) describes a more general approach to computation. They introduced the idea of laying down tiles of DNA to implement blocked cellular automata. After an initial sequence of DNA blocks is constructed with exposed sticky ends along one edge, free DNA blocks from the solution should precipitate out and anneal to matching sticky ends of the growing DNA crystal. The blocks can be designed to implement rules of cellular automata and thus the growth of the crystal can carry out a computation based on the state and input of the initial sequence of blocks (Winfree 1996; Winfree, Yang, and Seeman 1998). Winfree and coworkers (Winfree et al. 1998) dramatically demonstrated that it is possible both to construct two-dimensional blocks of DNA and to control their annealing into crystals in the plane.

Seeman's lab has gone even further to construct three-dimensional shapes (cubes and truncated octahedra), raising the possibility of computation through threedimensional cellular automata (Seeman et al. 1998). Alternatively, they suggest that Borromean rings of DNA could be used to carry out computation. Borromean rings are knots of n rings such that the removal of any single ring will disconnect other rings in the knot. A knot of 3 Borromean rings is shown in figure 5.10. If the closure of a strand of DNA into a ring represented the truth of a logical clause, then a conjunction of clauses could be represented by a Borromean ring. If any one clause were false, the whole would fall apart. Seeman and coworkers (Seeman et al. 1998) also show that information can be stored and manipulated in dsDNA through branch migration, as depicted in figure 5.11.

Figure 5.10: An example of three Borromean rings. Removing any one of the three rings will disconnect the other two.

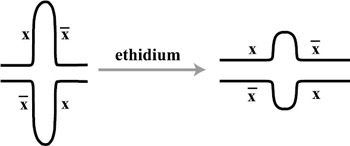
Figure 5.11: The migration of a branch in dsDNA can be controlled through the application of ethidium. In this case the ethidium applies torque to this cruciform and causes intrusion, a reduction of the hairpin bulges.

Khodor and Gifford (2000) have begun to develop a novel approach they call programmed mutagenesis. The idea is to place primers that represent rewrite rules into a PCR reaction and allow these rules to consecutively rewrite the template DNA. The primers not only initiate replication of the template, but the rewrite rules are slight mismatches, which nevertheless anneal to the template and are incorporated into the new strand that is being polymerized. Thus the slight alteration becomes part of the new template for copying. Khodor and Gifford (2000) described an algorithm for constructing a counter that takes as input a sequence XZZZZZ and incrementally replaces the Z subsequences with alternating X and Y subsequences of the same length. This process is depicted in figure 5.12.

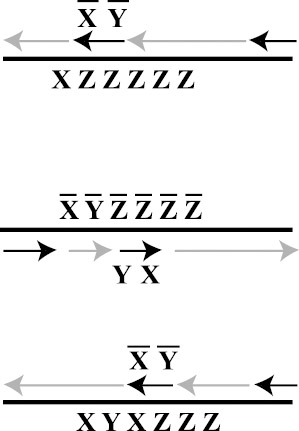
Figure 5.12: Three steps in the programmed mutagenesis of a counter. In the upper strand, the sequence XZZZZZ (representing 1) has an XY rewrite rule annealed to it (there is only a slight mismatch between Z and Y), as well as a standard PCR primer that catalyzes the construction of the template strand shown in the middle. The middle template strand now represents 2. It has the YX rewrite rule annealed to it. Again, X includes only a slight mismatch for annealing to Z. This causes the polymerization of the third template XYXZZZ which represents 3. The chain reaction will continue until the strand XYXYXY (6) has been constructed.

An ingenious form of DNA computation, dubbed whiplash PCR by Adleman, was introduced by Hagiya and coworkers (Hagiya et al. 1999). In whiplash PCR, computation is carried out within single strands of DNA that anneal to themselves, forming hairpins. Once a hairpin has formed, the presence of polymerase will extend the 3′ end. Control over consecutive reactions is attained by designing subsequences of the form <stop> <new state> <old state>. If the end of the strand has the encoding of <old state> then it will anneal to <old state> and the polymerase will extend the sequence from right to left, adding <new state> to the 3′ end. In fact, it would continue adding the complement of the strand to the end if it weren't for the <stop> sequence. The <stop> sequence is composed of bases whose complements are not available to the polymerase in the test tube. Thus the polymerization stops when it reaches the <stop> sequence. Once the <new state> sequence has been added to the 3′ end of the strand, there is a nonzero chance that it will melt off of its current position and form a new hairpin by annealing to a new transition sequence, as shown in figure 5.13. Sakamoto and coworkers (Sakamoto et al. 2000) and Winfree (Winfree 2000) generalized this technique to carry out any computation. Sakamoto and coworkers (Sakamoto et al. 2000) implemented a two-transition system and found that the optimal temperatures for the transitions were different.

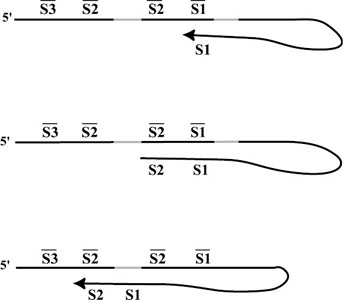
Figure 5.13: Three steps of a whiplash PCR reaction. The top strand shows the starting state (S1) with the 3′ end of the strand annealing to S1 and being extended by polymerase. In the middle strand, polymerase has added S2 to the 3′ end and halts at the stop sequence (shown in grey) because there are no available bases in the solution to construct the complement of the stop sequence. At some point the 3′ end melts away from the strand and then anneals to the beginning of the next transition (S3S2). This continues until there are no more possible transitions.

Conrad and Zauner (Conrad and Zauner 1999) suggest using the methylation of DNA as input channels of a gate, and its resulting chirality (B-DNA or Z-DNA) as the output of logic gates. Sequences that have the desired gate behavior could be evolved. Perhaps with control over sequence-specific methylation, these gates could be "wired up" to form a useful circuit. But for now, this remains a purely theoretical proposal.

Oliver (1996) described a process by which DNA could be made to implement matrix multiplication of Boolean or positive real valued matrices. The critical insight is that an m n matrix can be represented by a graph of m source nodes and n sink nodes with edges between every source and sink node that has a positive value. The multiplication of an m n by an n p matrix is then a matter of computing which of the p sink nodes can be reached from the m source nodes. Oliver suggests encoding an edge from node i to node j as a dsDNA with a unique sequence representing 〈ij〉 and sticky (single-stranded) ends. The sticky ends then allow 〈ij〉 to bind to 〈jk〉. With the addition of ligase, this forms the edges of the product m p matrix. Positive real values can be encoded as concentration of edges, with the result that (under appropriate conditions) the concentration of edges in the product matrix are the products of the edge concentrations in the operand matrices. Unfortunately, this approach has not been tested in the laboratory yet.

RNA has the interesting property that when it folds up into a three-dimensional shape, it can exhibit enzymatic activity (Landweber and Kari 2000). The powerful enzymatic activity was recently discovered in DNA as well (Santoro and Joyce 1997). The existence of these ribozymes (RNA) and DNA ribozymes (dioxyribozymes) suggest that it may well be possible to design computational systems wherein nucleic acids are both the data and the programs that manipulate that data (Kurtz et al. 1997).

The Search for the Killer Application One reason researchers are still floating new proposals of computational models for DNA is that no one has yet found the fountain of youth, the killer app, that will justify the value of DNA computation: "A killer app is an application that fits the DNA model; cannot be solved by the current or even future electronic machines; and is important" (Landweber, Lipton, and Rabin 1999: 161, emphasis theirs).

Even a solution that merely outperformed current electronic machines—though perhaps not future electronic machines—would probably still be considered a killer app. Boneh and coworkers (Boneh, Dunworth, and Lipton 1995) have made a start with a description of an algorithm for breaking the Data Encryption Standard (DES). This is just a variation on the Boolean circuit satisfiability algorithm. The algorithm only requires one example of a 64-bit sample of plain text and the encryption of that text to find a 56-bit DES key. The algorithm follows in three steps:

1. Generate all possible 56-bit keys.

2. For all keys in parallel, simulate the behavior of the DES circuit given that key and the 64-bit sample of plain text. (A description of such a circuit simulation is given above in the section entitled Generate and Test.) The DES circuit requires only a minor elaboration to handle xor gates and 64-entry lookup tables. The result of this is to append an encrypted version of the plain text to each strand of DNA representing a key.

3. Use the known encrypted version of the plain text to separate out all those keys that produce that encryption.

Boneh and coworkers (Boneh, Dunworth, and Lipton 1995) use the somewhat more conservative estimate that 10¹⁷ strands of DNA can fit in a liter of water. Thus (assuming all operations work perfectly, including the generation of the initial keys, all the separation steps involved in simulating the circuit, and extracting the answer strands) such a process can break any encryption algorithm that uses keys less than or equal to 57 bits. This is one bit more than necessary in the case of DES. Boneh and his coworkers claim the algorithm will work in the same amount of time for keys up to 64 bits long. This is predicted on a more optimistic estimate of the ability to manipulate 10²⁰ strands of DNA and would probably require more than a liter of water.

Assuming that they can set up a laboratory that can do 32 separations in parallel, a table lookup can be done in one of these parallel separation steps. Their algorithm requires a total of 916 separation steps (128 table lookups, 788 3 xor gates evaluated 3 at a time). With a rough estimate of 1 hour per separation step, and the calculation of 10 separation steps per day, DES could be broken in about 4 months of work. What is worse for those who rely on DES is that once this calculation is made, the results can be used repeatedly to locate other keys given the same pair of plain text and encrypted text under the new key. Adleman and coworkers (Adleman et al. 1996) developed a relatively error-tolerant algorithm for breaking DES using the sticker model and a mere gram of DNA. Yet these algorithms are currently out of our practical reach and may well depend on overly optimistic estimates of error rates.

Baum and Boneh (1996) suggest that rather than focusing on NP-complete problems, DNA might best be suited to dynamic programming problems. Dynamic programming problems generally involve a large number of constraints that must be simultaneously satisfied. This can be approached as a large number of subproblems that might be solved in parallel using the massive parallelism of DNA computation. Baum and Boneh give an algorithm for solving the graph connectivity problem (is there a path from a specified source node to a specified sink node in a graph?) as well as the knapsack problem (given a set of positive integers b₁, b₂, …, b_n and a target integer value B, is there a subset of those integers S such that ∑_i∈S^bi = B?), but note that DNA computing has difficulty implementing interprocess communication and so might be best at problems with relatively independent subproblems. But it is interesting to note that Blumberg (1999) has developed a model of just such interprocess communication.

Perhaps problems in traditional computer science do not provide the most fertile land of the settlers of DNA computation. Landweber and coworkers (Landweber, Lipton, and Rabin 1999) suggest that applying DNA computing to useful problems in the analysis of DNA itself may well provide the first killer apps. They suggest DNA fingerprinting, sequencing, and mutation screening as possible applications. They describe a method for translating an unknown input sequence into an encoded sequence with redundancy that can then by manipulated by the DNA tools described in the above section entitled Tools of the Trade. The guiding insight is that the tools of DNA computation are best at manipulating DNA, and so might be best applied to problems in the analysis of DNA. A further example of this is the work of Stemmer. Stemmer (1994) has shown that by removing the TEM-1 β-lactamase gene that confers antibiotic resistance to a strain of E. coli, cutting it into many pieces with DNase I, and then reassembling the pieces and reinserting into the E. coli, he was able to select for a 32,000-fold increase in antibiotic resistance!

Of Errors and Catastrophes

Many theoretical proposals have floundered on the shoals of practicality. A few studies have begun to quantify the error rates in our tools for manipulating DNA. The results are not encouraging. Failures in a DNA computation can derive from many problems:

Failure to generate the solution. If, in general, we assume that solution sequences of a generate-and-test algorithm are being created at random, then the problem of how much DNA you need, or how many solutions you need to generate, reduces to the coupon collector's problem. This problem states that if you want to collect the entire set of n different coupons by randomly drawing a coupon each trial, you can expect to make O(n log n) drawings before you collect the entire set. Similarly, the amount of DNA required to create all 2ⁿ potential binary solutions is actually O(n2ⁿ). This was first noted in Linial and Linial (1995). Bach and coworkers (Bach et al. 1996) show that Lipton's (1995) algorithm for generating random solutions reduces to the coupon collector's problem. Even though there is some bias in the process due to the equal amounts of "0" and "1" added to the test tube, the first 2ⁿ⁻¹ solutions form in a relatively unbiased fashion. Thus, in order to have a reasonable chance (1 − ε) of generating all possible solutions under Lipton's algorithm, you need to use O(n2ⁿ) DNA.

Breakage of the DNA in solution. DNA is not stable in water over long periods of time. It tends to break (hydrolyze). Furthermore, the mechanical shear of passing through a syringe puts a practical limit on sequence length of about 15 Kb (Smith 1995).

Failure of complementary strands to "find" each other. For two strands to anneal, they must bump into each other in the solution. This failure becomes more likely as problems are scaled up to real-world complexity with an exponential increase in the number of distinct strands in the solution. The time to anneal grows as the square root of the length of the strands and the reciprocal of the concentration of the desired "mates" (Smith 1995).

Failure to properly discriminate in annealing. In the process of exploring DNA computation on a surface, as opposed to in a solution, Liu and coworkers (Liu et al. 2000a) discovered that for a set of 16 different 16-mer sequences, only 9 of the complements could perfectly discriminate between the 16 target sequences at 37 C; the other 7 even annealed to some incorrect sequences at 40 C.

Yoshinobu and coworkers (Yoshinobu et al. 2000) examined errors in the process of annealing. They found that an 8-mer sequence could only tolerate a single base mismatch and still successfully anneal. They also noted that G and T readily annealed at a single mismatch locus. Let that be a warning for those who would design sequences for efficient and accurate DNA computations.

Failure of annealing due to secondary structure in the strands. If a strand of DNA (or RNA) has subsequences that complement each other, it will tend to fold up into hairpins and other secondary structures. This can prevent the desired annealing between strands.

Incorporation of incorrect bases during PCR. Polymerization in PCR is not error free. Depending on the polymerase enzyme used, the error can be as low as 7 10⁻⁷ per base pair (for Pfu) and as high as 2 10⁻⁴ per base pair (for Taq) (Cha and Thilly 1995). There is evidence that an alternative process, called the ligase chain reaction (LCR), does better than most PCR enzymes (Dieffenbach and Dveksler 1995).

Furthermore, PCR is designed with the assumption that the proportion of primer is far greater than the proportion of template in the solution. If there are a lot of templates, the interactions between the templates can interfere with the PCR (Kaplan, Cecci, Libchaber 1995). Kaplan and coworkers (Kaplan, Cecci, and Libchaber 1996) point out that the DNA computation literature tends to ignore the possibility for undesirable interactions between the various strands during the application of PCR. In particular, if an undesired 3′ end of a strand anneals to the middle of another strand, the polymerase will extend the 3′ end to complement the other strand. In general, this will cause a computational error. They demonstrate the hazards of PCR and those of gel electrophoresis by the production of supposedly "impossibly" long strands, which turned out to be an unanticipated hybridization of two desired strands. Finally, PCR may leave behind partially constructed strands in the solution. These may interfere with future manipulations.

Failure to extract a target sequence from a solution. Both Karp and coworkers (Karp, Kenyon, and Waarts 1995) and Roweis and coworkers (Roweis et al. 1998) replace a single separation with a series of separations. They trade off time and space (number of test tubes) for accuracy. If the separation step divides a set of DNA strands into a "true" test tube and a "false" test tube, the simplest version of this is to repeat the separation step on the "false" test tube, in order to lower the rate of false negatives. A more sophisticated version of this is to do repeated separations on both results, creating an array of test tubes 1, …, n, where test tube k contains all those strands that have been processed as "true" k times. Thus a DNA strand does a biased random walk across the array. Roweis and coworkers (Roweis et al. 1998) suggest fixing the size of the array and making absorbing boundaries out of the test tubes at the ends. They point out that any DNA strands that reach the boundary test tubes can immediately be used in the next step of the computation. This creates a form of pipelining. By increasing the size of the array and thus the number of separation steps that must be performed, the error rates can be made arbitrarily small.

Khodor and Gifford (1999) took a hard look at sequence separation based on biotinylation, with rigorous controls and measurements. Under ideal conditions, they were able to retrieve only 8–24 percent of the desired strands, although there were few false positives (<1%). This suggests that if sequence separation is called for in an algorithm, there must be many copies present of the desired sequence. Khodor and Gifford also note that if the target sequence is rare relative to the other sequences in the solution, even a small false positive rate will leave the target sequence in the minority in the resulting "positive" vial. These problems have prompted researchers to avoid sequence separation by annealing and instead use restriction enzymes to digest undesired sequences (Ouyang et al. 1997; Amos, Gibbors, and Hodgson 1998; Cukras et al. 2000).

Loss of DNA strands. It is known that DNA can stick to the walls of test tubes when a solution is poured from one tube into another. Khodor and Gifford (1999) found that significant portions of the population of DNA strands were completely lost in the process of sequence separation, appearing in neither the positive nor the negative test tubes after the separation. This implies that a sequence separation step of an algorithm should generally be followed by PCR amplification.

Failure of the split operation. If an algorithm relies on equally dividing the contents of a test tube into two test tubes, there is no guarantee that the copies of a particular sequence in the test tube will be equally divided between the two tubes. Bach and coworkers (Bach et al. 1996) model this with a "probabilistic split" operator and use their analysis to derive bounds on the amount of redundancy they need to find a desired solution with reasonable probability.

Failure to separate by length in a gel electrophoresis. This failure can result from a host of problems. Gels are not perfectly even in their porousness. Strands of DNA can stick to each other, or form secondary structures that affect their movement through the gel. They can also simply impede each other's progress in microscopic traffic jams. It can be extremely hard to separate strands of similar length. After two cycles of electrophoresis and PCR, Adleman had to repeat the electrophoresis four times on the product of the third PCR (Kaplan, Cecci, and Libchaber 1995), each time removing the 120-bp band in an attempt to reduce contamination.

Failure of restriction enzymes. Restriction enzymes might fail to cut the strands at their restriction sites due to lack of time, secondary structure in the strands, or other unknown interferences. Amos and coworkers (Amos et al. 1998) found that they were only able to destroy 2 out of 3 target sequences through the use of restriction enzymes. Their technique was to anneal a primer to the target sequence and then use a restriction enzyme that only cleaves dsDNA. Their failure thus may have been due to problems in annealing of the primer to the target sequence. In contrast, Wang and coworkers (Wang et al. 2000) report 97 percent efficiency of their restriction enzyme.

Failure of ligation due to secondary structure in the strands. Because ssDNA (and RNA) can fold up into complex shapes, these shapes may interfere with the ability of ligase to ligate the ends of two strands.

A Rocky Beginning Kaplan and coworkers (Kaplan, Cecci, and Libchaber 1995) set out to replicate Adleman's original experiment and failed. Or, to be more accurate, they state: "At this time, we have carried out every step of Adleman's experiment, but we have not gotten an unambiguous final result" (2). Adleman himself reported contamination of his 140-bp sample with 120-bp molecules. Kaplan and coworkers used both a positive and a negative control. The positive control was a simple graph with in-degree 1 and out-degree 1 for every node between v_in and v_out. This formed a single (Hamiltonian) path. The negative control was a graph identical to Adleman's except a single edge was removed, making the HPP unsolvable. They observed smears in their gels where there should have been distinct bands. Even the positive control, with such a simple structure, resulted in many different-length paths, including "impossible" paths longer than the total number of edges in the graph. When they cut out this path and ran it again on the gel, they found bands at 120bp and 140-bp, suggesting either contamination due to the shorter (faster) strands getting caught in the gel, or "an unusual configuration of 3 strands of partially hybridized DNA" (18). Kaplan and coworkers suggest that incomplete ligation, irregular ligation, heterogeneous sequence-dependent shapes of different paths, paths that break in the gel, temporary binding of proteins to the DNA in the gel, or single strands hanging off the ends may explain the smear.

Kazic (2000) points out that DNA is less stable than other molecules, hybridization is a low-yield reaction, and separation by gel is difficult and complicated by contamination.

^[3]Nucleotides form chains by connecting the 5′ position (5th carbon) in the five-carbon sugar ring (the pentose) to the 3′ position of the pentose in the next nucleotide. This gives a strand of DNA a particular direction with a free 3′ position at one end of the strand and a free 5′ position at the other end. The convention is to list the sequence of a DNA strand starting at the 5′ end and finishing at the 3′ end.

^[4]I will defer the problem of guaranteeing that all strings are actually generated until the section entitled of Errors and Catastrophes.

^[5]Lipton 1995, 543; I have altered the notation to preserve internal consistency.

^[6]The solution and accuracy of their technique was reported to me in a personal communication with Laura Landweber.

^[7]The 3-coloring problem is the problem of determining if the nodes of a graph can be colored such that no neighboring nodes have the same color, given only 3 colors.

^[8]It is a "one-pot" algorithm in theory. In implementation, Guarnieri, Fliss, and Bancroft added the terminal "carry" strand to the solution after they had carried out the addition on the first bit position of 1 + 1. So it still remains to be demonstrated how effective a chain reaction will be.