Merge Sort

We can use recursion to design sorting algorithms that are more efficient than insertion sort. This section describes one such algorithm, merge sort.

The recursive idea behind merge sort is:

1. If there is only one number to sort, do nothing.
2. Otherwise, divide the numbers into two groups. Recursively sort each group, then merge the two sorted groups into a single sorted array.

This process is illustrated in Figure 9-18.

Figure 9-18. In merge sort, the data to be sorted (top) are divided into two groups. Each group is recursively sorted. The results are then merged into the final result.

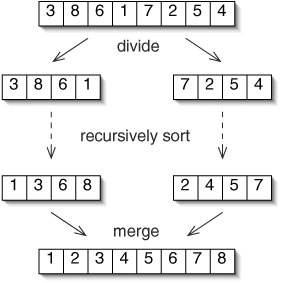
Merge sort is an example of a divide-and-conquer algorithm. In such an algorithm, we divide the data into smaller pieces, recursively conquer each piece, and then combine the results into a final result.

A sorting algorithm that modifies an existing array, such as insertion sort, is called an in-place sort. Merge sort is not an in-place sort. Instead, it returns a new array containing the numbers from the original array in sorted order. In the code for the main mergeSort() method (Figure 9-19), notice that the return type is int[].

Figure 9-19. The mergeSort() method returns a new array, rather than modifying data.

1 /**
2 * Return an array containing the numbers from data, in order from
3 * smallest to largest.
4 */
5 public static int[] mergeSort(int[] data) {
6 return mergeSortHelper(data, 0, data.length - 1);
7 }

Suppose we have a variable numbers that currently refers to some array of ints. If we want it to refer to a sorted version of that array, we have to invoke this method as:

numbers = mergeSort(numbers);

If we merely

mergeSort(numbers);

then numbers will not change; the sorted array is returned, but it hasn't been saved anywhere.

The method mergeSort() uses a recursive helper method (Figure 9-20). The arguments bottom and top indicate the region of the array to be sorted.

Figure 9-20. The recursive helper method mergeSortHelper().

 1 /**
 2 * Return an array containing the numbers in data between indices
 3 * bottom and top, inclusive, in order from smallest to largest.
 4 */
 5 protected static int[] mergeSortHelper(int[] data, int bottom,
 6 int top) {
 7 if (bottom == top) {
 8 return new int[] { data[bottom] };
 9 } else {

10 int midpoint = (top + bottom) / 2; 11 return merge(mergeSortHelper(data, bottom, midpoint), 12 mergeSortHelper(data, midpoint + 1, top)); 13 } 14 }

This code captures the algorithm with remarkable simplicity. The base case returns an array containing a single number. The recursive case merges the results of two recursive calls, each dealing with half of the region currently being sorted.

One more helper method, merge(), is needed. The job of this method is to combine two sorted arrays into one longer, sorted array (Figure 9-21).

Figure 9-21. The merging process combines two short sorted arrays into a longer one. At each step, the smallest element of either array is added to the end of the output array.

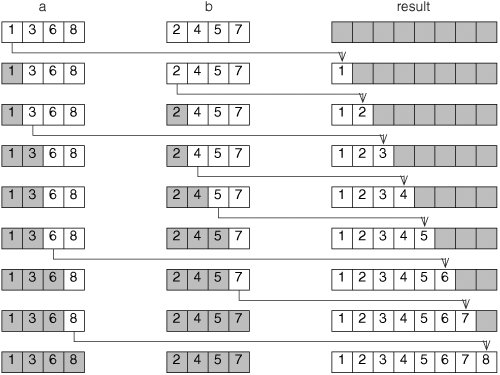
The merge() method (Figure 9-22) is not recursive, but is longer than either mergeSort() or mergeSortHelper(). It is not as complicated as it appears. The main loop on lines 816 fills up the array result by repeatedly taking the smallest element from the beginning of a or b. The indices i and j are indices into these arrays, telling where the next available element is. (This is the same trick we used with ArrayLists, but with the "not in use" portion at the left end of the array.) The complicated test on line 9 deals with the cases in which we've reached the end of one of the arrays. If array b is empty, we have to take the next element from a, and vice versa.

Figure 9-22. Once two arrays are sorted, this method merges them together.

 1 /**
 2 * Combine the two sorted arrays a and b into one sorted array.
 3 */
 4 protected static int[] merge(int[] a, int[] b) {
 5 int[] result = new int[a.length + b.length];
 6 int i = 0;
 7 int j = 0;
 8 for (int k = 0; k < result.length; k++) {
 9 if ((j == b.length) || ((i < a.length) && (a[i] <= b[j]))) {
10 result[k] = a[i];
11 i++;
12 } else {
13 result[k] = b[j];
14 j++;
15 }
16 }
17 return result;
18 }

Analysis of Merge Sort

Merge sort is more complicated than insertion sort. Is it worth the effort?

An invocation of merge() takes time linear in the total length of the resulting array. (The main loop always runs exactly n times.) The recurrence for mergeSortHelper(), assuming n is a power of 2, is:

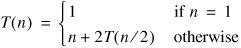
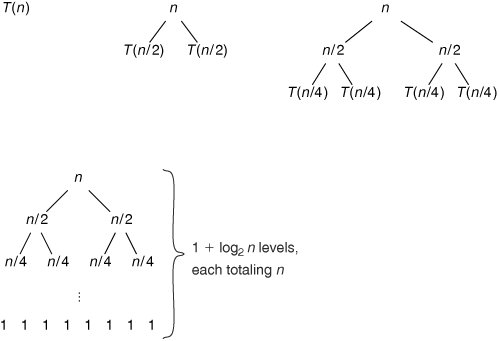
The solution is not obvious, so we expand a recurrence tree (Figure 9-23). It is clear that each level of the tree adds up to n. We need 1 + log2 n levels before we can convert the n copies of T(1) at the bottom into ones.

Figure 9-23. As the recursion tree for merge sort is expanded, each level adds up to n steps. The total number of levels is 1 + log2 n, so the entire tree adds up to n(1 + log2 n).

(This item is displayed on page 239 in the print version)

This gives a total running time of:

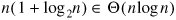
This is a strictly lower order than the quadratic running time of insertion sort, so merge sort is faster for sorting large arrays.

Exercises

9.9	Explain the three arguments passed to mergeSortHelper() in line 6 of Figure 9-19.
9.10	Write a mergeSort() method for the SortableArrayList class from Section 8.4. Your method should invoke some kind of mergeSortHelper() to get a new, sorted list, but it should not simply return this result. Instead, it should copy the elements in this new list back into the original SortableArrayList. How does this affect the running time of mergeSort()?
9.11	Is the analysis of merge sort for the best, worst, or average case? Explain.
9.12	Write a recurrence for the total size of all the arrays created during an invocation of mergeSortHelper(). What is the solution to this recurrence?

Quicksort