Disjoint Set Clusters

This section introduces a data structure for representing a cluster of disjoint sets. Sets are disjoint if they have no elements in common. Clusters of disjoint sets include the sets of players on different baseball teams, the sets of cities in different countries, and the sets of newspapers owned by different media companies. They also play a crucial role in an algorithm we will see in Section 15.6.

We could use several instances of implementations of the Set interface. The alternate data structure described here allows us to more efficiently perform the following operations:

• Determine whether two elements belong to the same set.
• Merge two sets.

A cluster of sets is represented as a forest of trees (Figure 14-11). If two elements are in the same tree, they are in the same set. Unlike trees we've seen in the past, nodes in these trees keep track of their parents, rather than their children. They are therefore sometimes called up-trees.

Figure 14-11. A forest of up-trees representing the disjoint sets {1, 3, 4, 5}, {6, 9}, and {0, 2, 7, 8}.

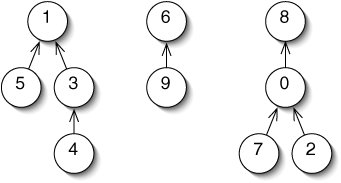
To determine if two elements are in the same set, we follow the arrows up from each element up to a root. If they lead to the same root, the elements are in the same tree.

To merge two sets, we make the root of one tree point to the root of the other tree (Figure 14-12).

Figure 14-12. After merging, there are only two sets: {1, 3, 4, 5, 6, 9} and {0, 2, 7, 8}.

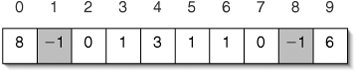
We could represent the up-trees with linked structures, but if we assume that the elements are ints in the range 0 through n 1, we can use a more efficient contiguous structure (Figure 14-13). At each position, we store the parent of the corresponding element. For example, since 8 is the parent of 0, we store 8 at index 0. The special value 1 is used for roots, which have no parent.

Figure 14-13. Contiguous representation of the up-trees in Figure 14-12. Each position holds the parent of the corresponding element, or 1 if there is no parent.

The code for this implementation is given in Figure 14-14. All of the methods take constant time except for findRoot(). In the worst case (a single, linear tree), this takes time in Q(n). The techniques described next ensure that the trees are shallow and wide, making the paths shorter.

Figure 14-14. First draft of the DisjointSetCluster class.

 1 /** A cluster of disjoint sets of ints. */
 2 public class DisjointSetCluster {
 3
 4 /** parents[i] is the parent of element i. */
 5 private int[] parents;
 6
 7 /** Initially, each element is in its own set. */
 8 public DisjointSetCluster(int capacity) {
 9 parents = new int[capacity];
10 for (int i = 0; i < capacity; i++) {
11 parents[i] = -1;
12 }
13 }
14
15 /** Return the index of the root of the tree containing i. */
16 protected int findRoot(int i) {
17 while (!isRoot(i)) {
18 i = parents[i];
19 }
20 return i;
21 }
22
23 /** Return true if i and j are in the same set. */
24 public boolean inSameSet(int i, int j) {
25 return findRoot(i) == findRoot(j);
26 }
27
28 /** Return true if i is the root of its tree. */
29 protected boolean isRoot(int i) {
30 return parents[i] < 0;
31 }
32
33 /** Merge the sets containing i and j. */
34 public void mergeSets(int i, int j) {
35 parents[findRoot(i)] = findRoot(j);
36 }
37
38 }

Merging by Height

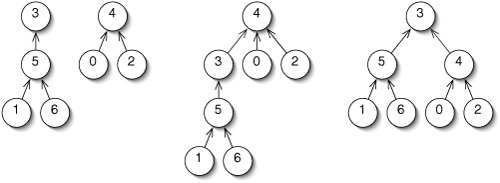
When we merge two up-trees, we have to choose which root becomes a child of the other root (Figure 14-15). Instead of doing this arbitrarily, we can keep the trees shorter by making the root of the shorter tree a child of the root of the taller tree. This is called merging by height.

Figure 14-15. The two up-trees at left are to be merged. We could merge the taller one into the shorter one (middle) or vice versa (right). The result on the right is better because it is a shorter tree.

To do this, we need to keep track of the height of each tree. There is a clever way to do this without using any more memory. We need to keep track of heights only for the roots. These are exactly the nodes which don't have parents. We can therefore store the height of each root in the array parents.

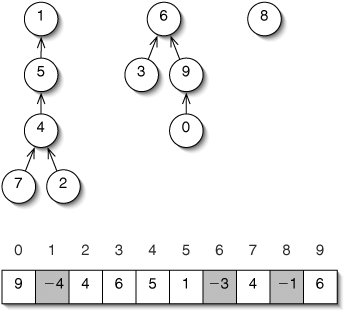
To avoid confusion between a root with height 3 and a node whose parent is 3, we store the heights as negative numbers (Figure 14-16). We have to subtract one from all of these negative numbers, because a tree might have height 0 and there is no such int as 0. Thus, the entry for the root of a tree of height h is h 1.

Figure 14-16. For height merging, we must keep track of the height of each tree. The entry in parents for the root of a tree of height h is h 1.

(This item is displayed on page 380 in the print version)

The improved version of mergeSets() is shown in Figure 14-17.

Figure 14-17. The mergeSets() method using height merging.

1 /** Merge the sets containing i and j. */
2 public void mergeSets(int i, int j) {
3 if (parents[i] > parents[j]) {
4 parents[findRoot(i)] = findRoot(j);
5 } else {
6 if (parents[i] == parents[j]) {
7 parents[i]--;
8 }
9 parents[findRoot(j)] = findRoot(i);
10 }
11 }

Path Compression

A second improvement to up-trees involves the findRoot() method. Suppose we determine that the root of the tree containing 4 is 7. We can make this operation faster next time by making 7 the parent of 4 (Figure 14-18). In fact, we might as well make 7 the parent of every node we visit on the way to the root. This technique is called path compression.

Figure 14-18. The root of the tree containing 4 is 7 (top). Using path compression, we reset the parent of every node visited in determining this to 7, making the tree shorter.

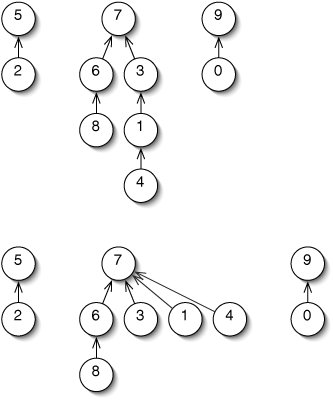
In writing the code for path compression, we realize that we can't alter these parents until after we've found the root. Since this involves remembering work we still have to do, this algorithm is most clearly expressed recursively (Figure 14-19).

Figure 14-19. The findRoot() method with path compression.

1 /** Return the index of the root of the tree containing i. */
2 protected int findRoot(int i) {
3 if (isRoot(i)) {
4 return i;
5 }
6 parents[i] = findRoot(parents[i]);
7 return parents[i];
8 }

Path compression may render the height counts inaccurate, but they are still legitimate upper bounds on the heights of the trees.

The analysis of up-trees with these improvements is beyond the scope of this book, but the result is impressive. The amortized running times of findRoot() and mergeSets() are in O(log* n), where log* n is the number of times we have to take the logarithm to get down to 1. In other words, log* n is to log n what log2 n is to n/2. This is an incredibly slowly-growing function (Figure 14-20). For all practical purposes, the amortized running time of up-tree operations is constant.

Figure 14-20. The log* function (assuming base 2 logarithms).

n	log* n
2	1
4	2
16	3
65536	4
265536	5

 

Exercises

14.5	Which order is higher: Q(log (log n)) or Q(log* n)?
14.6	How could we store a cluster of disjoint sets of Strings? (Hint: Don't modify the DisjointSetCluster class; use an additional data structure.)
14.7	Can we have an empty set in a DisjointSetCluster? If so, how? If not, why not?
14.8	Can we traverse the elements of a DisjointSetCluster? If so, how? If not, why not?