Best, Worst, and Average Case
Figure 7-17 shows the contains() method from our ArrayList class. It is difficult to analyze because of the if statement on line 3. The method clearly takes time linear in size if we have to search through all of the elements in the ArrayList, but it might take much less if the element at position 0 happens to be equals() to target. The running time depends not only on the size of the data structure, but also on its contents.
Figure 7-17. The running time for the contains() method from our ArrayList class depends on the contents of the ArrayList.
1 public boolean contains(E target) {
2 for (int i = 0; i < size; i++) {
3 if (data[i].equals(target)) {
4 return true;
5 }
6 }
7 return false;
8 }
|
At this point, we have to decide which kind of analysis we're doing. The easiest, but least useful, is best-case analysis. This tells us how fast the program runs if we get really lucky about the data. For contains(), the best case occurs when the first item in the list is target. The best-case running time is Q(1).
Best-case analysis is not very reassuring. An algorithm might shine in some incredibly rare circumstance but have lousy performance in general.
More useful is worst-case analysis: at any if statement, take the more expensive branch. For contains(), this means assuming that target is not in the ArrayList, giving a running time of Q(n). It is only a slight abuse of the notation to simply say that contains() takes time in O(n)it might be in Q(n) or it might be in a lower order.
We can also perform average-case analysis. This is tricky, as it requires that we make some assumption about what the "average" data set looks like.
Given a set of different events which might occur, the average running time is:
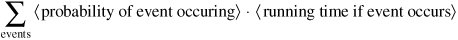
We must always be careful to choose our events so that they are exhaustive (at least one of them will occur) and mutually exclusive (no more than one of them will occur).
To analyze the average performance of contains(), let's assume that target is present exactly once, but is equally likely to be at any index in the ArrayList. The appearance of target at any particular index is an event. There are n different possible events, and we assume that they are equally likely. Thus, the probability of each event occurring is 1/n.
If target is at index 0, there is one pass through the loop. If target is at index 1, there are two passes, and so on. The average running time for contains() is therefore:
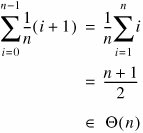
Notice that this is the same order as the worst-case running time, but not as good as the best case. It is always true that:
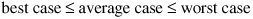
Consequently, if the best and worst cases are in the same order, the average case must also be in that order.
Exercises
| 7.13 |
What is the average result of rolling a 6-sided die? |
|
| 7.14 |
We want to know the average output (not running time) of the method in Figure 7-18. We might try to do this by determining the average result of rolling a die and then squaring that. What's wrong with this reasoning? Figure 7-18. Code for Exercise 7.14. The average output of this method is not simply the square of the average die roll.
|
Amortized Analysis |
Part I: Object-Oriented Programming
Encapsulation
Polymorphism
Inheritance
- Inheritance
- Extending a Class
- The Object Class
- Packages and Access Levels
- Summary
- Vocabulary
- Problems
- Projects
Part II: Linear Structures
Stacks and Queues
- Stacks and Queues
- The Stack Interface
- The Call Stack
- Exceptions
- The Queue Interface
- Summary
- Vocabulary
- Problems
- Projects
Array-Based Structures
- Array-Based Structures
- Shrinking and Stretching Arrays
- Implementing Stacks and Queues
- The List Interface
- Iterators
- The Java Collections Framework: A First Look
- Summary
- Vocabulary
- Problems
- Projects
Linked Structures
- Linked Structures
- List Nodes
- Stacks and Queues
- The LinkedList Class
- The Java Collections Framework Revisited
- Summary
- Vocabulary
- Problems
- Projects
Part III: Algorithms
Analysis of Algorithms
- Analysis of Algorithms
- Timing
- Asymptotic Notation
- Counting Steps
- Best, Worst, and Average Case
- Amortized Analysis
- Summary
- Vocabulary
- Problems
- Projects
Searching and Sorting
- Searching and Sorting
- Linear Search
- Binary Search
- Insertion Sort
- The Comparable Interface
- Sorting Linked Lists
- Summary
- Vocabulary
- Problems
- Projects
Recursion
- Recursion
- Thinking Recursively
- Analyzing Recursive Algorithms
- Merge Sort
- Quicksort
- Avoiding Recursion
- Summary
- Vocabulary
- Problems
- Projects
Part IV: Trees and Sets
Trees
Sets
- Sets
- The Set Interface
- Ordered Lists
- Binary Search Trees
- Hash Tables
- The Java Collections Framework Again
- Summary
- Vocabulary
- Problems
- Projects
Part V: Advanced Topics
Advanced Linear Structures
- Advanced Linear Structures
- Bit Vectors
- Sparse Arrays
- Contiguous Representation of Multidimensional Arrays
- Advanced Searching and Sorting
- Summary
- Vocabulary
- Problems
- Projects
Strings
Advanced Trees
- Advanced Trees
- Heaps
- Disjoint Set Clusters
- Digital Search Trees
- Red-Black Trees
- Summary
- Vocabulary
- Problems
- Projects
Graphs
- Graphs
- Terminology
- Representation
- Graph Traversal
- Topological Sorting
- Shortest Paths
- Minimum Spanning Trees
- Summary
- Vocabulary
- Problems
- Projects
Memory Management
Out to the Disk
- Out to the Disk
- Interacting with Files
- Compression
- External Sorting
- B-Trees
- Summary
- Vocabulary
- Problems
- Projects
Part VI: Appendices
A. Review of Java
- A. Review of Java
- A.1. The First Program
- A.2. Variables and Types
- A.3. Loops
- A.4. Interacting with the User
- A.5. Branching
- A.6. Methods and Breaking Out
- A.7. Constants
- A.8. Operators
- A.9. Debugging
- A.10. Coding Conventions
B. Unified Modeling Language
C. Summation Formulae
- C. Summation Formulae
- C.1. Sum Notation
- C.2. Sum of Constants
- C.3. Sum of First n Integers
- C.4. Sums of Halves and Doubles
- C.5. Upper Limit on Sum of a Function
- C.6. Constant Factors
D. Further Reading
Index
EAN: 2147483647
Pages: 216
