Generating Nonlinear Curve Fits Using Excel Charts
Problem
You'd like to generate best-fit curvesnonlinear curvesthrough your data.
Solution
Use Excel's chart trendline feature to perform nonlinear curve fits of your data. Plot your data using an XY scatter chart (see Chapter 4). Once your chart has been created, right-click on the data series and select Add Trendline from the pop-up menu.
Discussion
The procedure for adding nonlinear trendlines to charts is the same as that used for adding linear trendlines, as discussed in Recipe 8.1. Once you've plotted your data using an XY scatter chart, you can generate a trendline, which will be displayed on the chart, superimposed over your data. You can also include the resulting equation for the best-fit line on your chart.
When you add a trendline using the procedure discussed in Recipe 8.1, you can choose from several different Trend/Regression types (as shown in the Add Trendline dialog box in Figure 8-1). Depending on the range of values in your data, you'll be able to choose from six different trendlines. Of these six, four are nonlinear trendlines: Logarithmic, Polynomial, Power, and Exponential. The other two include the Linear trendline already discussed and a Moving Average trendline.
The Logarithmic trendline uses the equation:

where c and b are parameters to be determined during the curve-fitting process.
Polynomial trendlines use the equation:
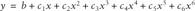
where the c-coefficients and b are parameters of the curve fit. Excel supports polynomial fits up to sixth order. You can select the order to use in the Add Trendline dialog box (See Figure 8-1).
Excel's Power trendline uses the equation:
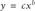
where c and b are parameters of the fit.
Finally, the Exponential trendline uses the equation:
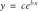
where c and b are parameters of the fit.
The natural question that arises upon learning of these available models is which one to use. There's no single answer to this question, as it depends on your purpose for performing the fit and the nature of your data. If you're simply fitting a curve through some data so you can conveniently interpolate the data, then choose whichever model best replicates your data. In this case, you're not so concerned with smoothing the data or with statistical rigor. To assess which model works, you can look at the R-squared value (see Recipe 8.7) or you can eyeball the trendline against your data. Further, you can plot the residualsdifferences between your actual y-value and the estimated y-valueand examine them to assess how well your data is represented. You can compute percentage differences to gauge how well your data is replicated. Further, you should examine how the trendline behaves between data points used to generate the trendline to make sure there are no unrealistic oscillations between data points. This can happen when you try to fit a higher-order polynomial trendline.
On the other hand, if you're genuinely interested in modeling the data from a statistical standpoint, or are trying to gain insight in a physical process, then I suggest you read Recipe 8.7. Further, you must also consider what your data represents. If your data represents some physical process, then let physics be your guide and choose a model that best represents the physical relationship between the variables underlying the data, if it is indeed known. If none of Excel's trendline models work for you, then you're left to your own devices to craft a suitable model. In this case, take a look at Recipe 8.6.
See Also
Take a look at Recipes 8.6 and 8.7. Also, be sure to read Recipe 8.1 for a refresher on adding trendlines to charts.
Using Excel
- Introduction
- Navigating the Interface
- Entering Data
- Setting Cell Data Types
- Selecting More Than a Single Cell
- Entering Formulas
- Exploring the R1C1 Cell Reference Style
- Referring to More Than a Single Cell
- Understanding Operator Precedence
- Using Exponents in Formulas
- Exploring Functions
- Formatting Your Spreadsheets
- Defining Custom Format Styles
- Leveraging Copy, Cut, Paste, and Paste Special
- Using Cell Names (Like Programming Variables)
- Validating Data
- Taking Advantage of Macros
- Adding Comments and Equation Notes
- Getting Help
Getting Acquainted with Visual Basic for Applications
- Introduction
- Navigating the VBA Editor
- Writing Functions and Subroutines
- Working with Data Types
- Defining Variables
- Defining Constants
- Using Arrays
- Commenting Code
- Spanning Long Statements over Multiple Lines
- Using Conditional Statements
- Using Loops
- Debugging VBA Code
- Exploring VBAs Built-in Functions
- Exploring Excel Objects
- Creating Your Own Objects in VBA
- VBA Help
Collecting and Cleaning Up Data
- Introduction
- Importing Data from Text Files
- Importing Data from Delimited Text Files
- Importing Data Using Drag-and-Drop
- Importing Data from Access Databases
- Importing Data from Web Pages
- Parsing Data
- Removing Weird Characters from Imported Text
- Converting Units
- Sorting Data
- Filtering Data
- Looking Up Values in Tables
- Retrieving Data from XML Files
Charting
- Introduction
- Creating Simple Charts
- Exploring Chart Styles
- Formatting Charts
- Customizing Chart Axes
- Setting Log or Semilog Scales
- Using Multiple Axes
- Changing the Type of an Existing Chart
- Combining Chart Types
- Building 3D Surface Plots
- Preparing Contour Plots
- Annotating Charts
- Saving Custom Chart Types
- Copying Charts to Word
- Recipe 4-14. Displaying Error Bars
Statistical Analysis
- Introduction
- Computing Summary Statistics
- Plotting Frequency Distributions
- Calculating Confidence Intervals
- Correlating Data
- Ranking and Percentiles
- Performing Statistical Tests
- Conducting ANOVA
- Generating Random Numbers
- Sampling Data
Time Series Analysis
- Introduction
- Plotting Time Series Data
- Adding Trendlines
- Computing Moving Averages
- Smoothing Data Using Weighted Averages
- Centering Data
- Detrending a Time Series
- Estimating Seasonal Indices
- Deseasonalization of a Time Series
- Forecasting
- Applying Discrete Fourier Transforms
Mathematical Functions
- Introduction
- Using Summation Functions
- Delving into Division
- Mastering Multiplication
- Exploring Exponential and Logarithmic Functions
- Using Trigonometry Functions
- Seeing Signs
- Getting to the Root of Things
- Rounding and Truncating Numbers
- Converting Between Number Systems
- Manipulating Matrices
- Building Support for Vectors
- Using Spreadsheet Functions in VBA Code
- Dealing with Complex Numbers
Curve Fitting and Regression
- Introduction
- Performing Linear Curve Fitting Using Excel Charts
- Constructing Your Own Linear Fit Using Spreadsheet Functions
- Using a Single Spreadsheet Function for Linear Curve Fitting
- Performing Multiple Linear Regression
- Generating Nonlinear Curve Fits Using Excel Charts
- Fitting Nonlinear Curves Using Solver
- Assessing Goodness of Fit
- Computing Confidence Intervals
Solving Equations
- Introduction
- Finding Roots Graphically
- Solving Nonlinear Equations Iteratively
- Automating Tedious Problems with VBA
- Solving Linear Systems
- Tackling Nonlinear Systems of Equations
- Using Classical Methods for Solving Equations
Numerical Integration and Differentiation
- Introduction
- Integrating a Definite Integral
- Implementing the Trapezoidal Rule in VBA
- Computing the Center of an Area Using Numerical Integration
- Calculating the Second Moment of an Area
- Dealing with Double Integrals
- Numerical Differentiation
Solving Ordinary Differential Equations
- Introduction
- Solving First-Order Initial Value Problems
- Applying the Runge-Kutta Method to Second-Order Initial Value Problems
- Tackling Coupled Equations
- Shooting Boundary Value Problems
Solving Partial Differential Equations
- Introduction
- Leveraging Excel to Directly Solve Finite Difference Equations
- Recruiting Solver to Iteratively Solve Finite Difference Equations
- Solving Initial Value Problems
- Using Excel to Help Solve Problems Formulated Using the Finite Element Method
Performing Optimization Analyses in Excel
- Introduction
- Using Excel for Traditional Linear Programming
- Exploring Resource Allocation Optimization Problems
- Getting More Realistic Results with Integer Constraints
- Tackling Troublesome Problems
- Optimizing Engineering Design Problems
- Understanding Solver Reports
- Programming a Genetic Algorithm for Optimization
Introduction to Financial Calculations
- Introduction
- Computing Present Value
- Calculating Future Value
- Figuring Out Required Rate of Return
- Doubling Your Money
- Determining Monthly Payments
- Considering Cash Flow Alternatives
- Achieving a Certain Future Value
- Assessing Net Present Worth
- Estimating Rate of Return
- Solving Inverse Problems
- Figuring a Break-Even Point
Index
EAN: 2147483647
Pages: 206
