10.4 First-Order Conditional Logic

In Section 8.6 a number of different approaches to giving semantics to conditional logic, including possibility structures, ranking structures, PS structures (sequences of probability sequences), and preferential structures, were all shown to be characterized by the same axiom system, AX^cond_n, occasionally with C5 and C6 (as defined in Section 8.6) added, as appropriate. This suggests that all the different semantic approaches are essentially the same, at least as far as conditional logic is concerned. A more accurate statement would be that these approaches are the same as far as propositional conditional logic is concerned. Some significant differences start to emerge once the additional expressive power of first-order quantification is allowed. Again, plausibility is the key to understanding the differences.

Just as with probabilistic reasoning, for all these approaches, it is possible to consider a "degrees of belief" version, with some measure of likelihood over the possible worlds, and a "statistical" version, with some measure of likelihood on the domain. For the purposes of this section, I focus on the degrees of belief version. There are no new issues that arise for the statistical version, beyond those that already arise in the degrees of belief version. Perhaps the most significant issue that emerges in firstorder conditional logic is the importance of allowing structures with not only infinite domains but infinitely many possible worlds.

Let ^qual,fo_n, ^ps,fo_n, ^poss,fo_n, ^poss⁺,fo_n, ^rank,fo_n, ^pref⁺,fo_n, and ^pref,fo_n be the class of all relational qualitative plausibility structures, PS structures, possibility structures, possibility structures where the possibility measure satisfies Poss3⁺, ranking structures, ranking structures where the ranking function satisfies Rk3⁺, and preferential structures, respectively, for n agents. Let _n^→,fo(풯) be the obvious first-order analogue of the _n^→(Φ).

I start with plausibility, where things work out quite nicely. Clearly the axioms of AX^cond_n and AX^fo are sound in ^qual,fo_n. To get completeness, it is also necessary to include the analogue of IV. Let N_iφ be an abbreviation for φ →_i false. It is easy to show that if M = (W, D, 풫₁,…, 풫_n, π) ∈ ^qual,fo, then (M, w) ⊨ N_iφ iff Pl_{w, i}([[ φ]]_M) = ⊥; that is, N_iφ asserts that the plausibility of φ is the same as that of the empty set, so that φ is true "almost everywhere" (Exercise 10.15). Thus, N_iφ is the plausibilistic analogue of ℓ_i(φ) = 1. Let AX^cond,fo consist of all the axioms and inference rules of AX^cond (for propositional reasoning about conditional logic) and AX^fo, together with the plausibilistic version of IV:

The validity of IVPl in ^qual,fo follows from the fact that variables are rigid, just as in the case of probability (Exercise 10.16).

Theorem 10.4.1

AX^{cond, fo}_n is a sound and complete axiomatization with respect to ^qual,fo_n for the language _n^→,fo.

In the propositional case, adding C6 to AX^cond_n gives a sound and complete axiomatization of _n^→ with respect to PS structures (Theorem 8.6.5). The analogous result holds in the first-order case.

Theorem 10.4.2

AX^cond,fo_n + {C6} is a sound and complete axiomatization with respect to ^ps,fo_n for the language_n^→,fo.

Similarly, I conjecture that AX^cond,fo_n + {C5, C6} is a sound and complete axiomatization with respect to ^poss,fo_n for the language _n^→,fo, although this has not been proved yet.

What about the other types of structures considered in Chapter 8? It turns out that more axioms besides C5 and C6 are required. To see why, recall the lottery paradox (Example 8.1.2).

Example 10.4.3

The key characteristics of the lottery paradox are that any particular individual is highly unlikely to win, but someone is almost certainly guaranteed to win. Thus, the lottery has the following two properties:

Let the formula Lottery be the conjunction of (10.2) and (10.3). (I am assuming here that there is only one agent doing the reasoning, so I drop the subscript on →.)

Lottery is satisfiable in ^qual,fo₁. Define M_lot = (W_lot, D_lot, 풫_lot, π_lot) as follows:

D_lot is a countable domain consisting of the individuals d₁, d₂, d₃, …;
w_lot consists of a countable number of worlds w₁, w₂, w₃, …;
풫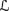_lot(w) = (W_lot, Pl_lot), where Pl_lot gives the empty set plausibility 0, each nonempty finite set plausibility 1/2, and each infinite set plausibility 1;
π_lot is such that in world w_i the lottery winner is individual d_i (i.e., Winner^πlot(wi) is the singleton set {d_i}).

It is straightforward to check that Pl_lot is qualitative (Exercise 10.17). Abusing notation slightly, let Winner(d_i) be the formula that is true if individual d_i wins. (Essentially, I am treating d_i as a constant in the language that denotes individual d_i ∈ D_lot in all worlds.) By construction, [[ Winner(d_i)]]_M^lot = W −{w_i}, so

That is, the plausibility of individual d_i losing is greater than the plausibility of individual d_i winning, for each d_i ∈ D_lot. Thus, M_lot satisfies (10.2). On the other hand, [[∃xWinner(x)]]_{M_lot} = W, so Pl_lot([[∃xWinner(x)]]_{M_lot})> Pl_lot([[ ∃xWinner(x)]]_{M_lot}); hence, M_lot satisfies (10.3).

It is also possible to construct a relational PS structure (in fact, using the same set w_lot of worlds and the same interpretation π_lot) that satisfies Lottery (Exercise 10.18). On the other hand, there is no relational ranking structure in ^rank⁺,fo₁ that satisfies Lottery. To see this, suppose that M = (W, D, 풜풩풦, π) ∈ ₁^rank⁺,fo and (M, w) ⊨ Lottery. Suppose that 풜풩풦(w) = (W′, κ). For each d ∈ D, let w_d be the subset of worlds in W′ where d is the winner of the lottery; that is, W_d = {w ∈ w′ : d ∈ Winner^π(w)}. It must be the case that κ(W′ − W_d) <κ(W_d) (i.e., κ(W′ ∩ [[ Winner(d)]]_M)< κ(W′ ∩ [[Winner(d)]]_M)), otherwise (10.2) would not be true at world w. Let w₀ be a world in w′ such that κ(w₀) = 0. (It easily follows from Rk3⁺ that there must be some world with this property; there may be more than one.) Clearly w₀ ∉ W_d for all d ∈ D, for otherwise κ(W_d) = 0 ≤ κ(W′ − W_d). That means no individual d wins in w₀; that is, Winner^π(w₀) =∅. Thus, w₀ ∈ [[ ∃xWinner(x)]]_M ∩ W′. But that means that

so (M, w) ⊭ true →∃xWinner(x). This contradicts the initial assumption that (M, w) ⊨ Lottery.

There is a ranking structure in ₁^rank,fo that satisfies Lottery. It is essentially the same as the plausibility structure that satisfies Lottery. Consider the relational ranking structure M₁ = (W_lot, D_lot, 풜풩풦, π_lot) where all the components except for 풜풩풦 are the same as in the plausibility structure M_lot, and 풜풩풦(w) = (W_lot, κ), where κ(U) is 0 if U is infinite, 1 if U is a finite and nonempty, and ∞ if U = ∅. It is easy to check that M₁ satisfies lottery, for essentially the same reasons that M_lot does.

There is also a relational possibility structure in ^poss⁺,fo_n that satisfies Lottery. Consider the relational possibility structure M₂ = (W_lot, D_lot, 풫풪풮풮, π_lot), where all the components besides 풫풪풮풮 are just as in the plausibility structure M_lot, 풫풪풮풮(w) = (W_lot, Poss), Poss(w_i) = i/(i + 1), and Poss is extended to sets so that Poss(U) = sup_w∈U Poss(w). (This guarantees that Poss3⁺ holds.) Thus, if i > j, then it is more possible that individual d_i wins than individual d_j. Moreover, this possibility approaches 1 as i increases. It is not hard to show that M₂ satisfies Lottery (Exercise 10.19).

As in Section 2.7 (see also Exercise 2.51), Poss determines a total order on W defined by taking w ≽ w′ if Poss(w) ≥ Poss(w′). According to this order, … ≻ w₃ ≻ w₂ ≻ w₁. There is also a preferential structure in ^pref,fo_n that uses this order and satisfies Lottery (Exercise 10.20).

Although Lottery is satisfiable in ^pass⁺,fo₁, ^pref,fo₁, and ^rank,fo₁, slight variants of it are not, as the following examples show:

Example 10.4.4

Consider a crooked lottery, where there is one individual who is more likely to win than any of the others, but who is still unlikely to win. This can be expressed using the following formula Crooked:

The first conjunct of Crooked states that each individual has some plausibility of winning; in the language of plausibility, this means that if (M, w) ⊨ Crooked, then Pl(W_w ∩ [[Winner(d) ]]_M)> ⊥ for each domain element d. Roughly speaking, the second conjunct states that there is an individual who is at least as likely to win as anyone else. More precisely, it says if (M, w) ⊨ Crooked, d* is the individual guaranteed to exist by the second conjunct, and d is any other individual, then it must be the case that Pl(W_w ∩ [[Winner(d) ∧ Winner(d*)]]_M)< Pl(W_w ∩ [[Winner(d*)]]_M). This follows from the observation that if (M, w) ⊨ (φ ∨ ψ) → ψ, then either Pl(W_w ∩ [[φ ∨ ψ]]_M) = ⊥ (which cannot happen for the particular φ and ψ in the second conjunct because of the first conjunct of Crooked) or Pl(W_w ∩ [[φ ∧ ψ]]_M) < Pl(W_w ∩ [[ψ]]_M).

Take the crooked lottery to be formalized by the formula Lottery ∧ Crooked.Itis easy to model the crooked lottery using plausibility. Consider the relational plausibility structure M′_lot = (W_lot, D_lot, 풫′_lot, π_lot), which is identical to M_lot except that 풫′_lot(w) = (W, Pl′_lot), where

Pl′_lot(∅) = 0;
if A is finite, then Pl′_lot(A) = 3/4 if w₁ ∈ A and Pl′_lot(A) = 1/2 if w₁ ∉ A;
if A is infinite, then Pl′_lot(A) = 1.

It is easy to check that Pl′_lot is qualitative, that M′_lot satisfies Crooked, taking d₁ to be the special individual whose existence is guaranteed by the second conjunct (since Pl′_lot([[Winner(d₁)]]_{M′_lot}) = 3/4 > 1/2 = Pl′_lot([[Winner(d_i) ∩ Winner(d₁)]]_{M′_lot}) for i > 1), and that Pl′_lot ⊨ Lottery (Exercise 10.21). Indeed, Pl′_lot is a possibility measure, although it does not satisfy Poss3⁺, so M′_lot ∉ ^poss⁺,fo_n. In fact, Lottery ∧ Crooked is not satisfiable in either ^poss⁺,fo_n or ^pref,fo_n (Exercise 10.22). Intuitively, the problem in the case of possibility measures is that the possibility of d₁ winning has to be at least as great as that of d_i winning for i ≠ 1, yet it must be less than 1. However, the possibility of someone winning must be 1. This is impossible. A similar problem occurs in the case of preferential structures.

Example 10.4.5

Consider a rigged lottery, where for every individual x, there is an individual y who is more likely to win than x. This can be expressed using the following formula Rigged, which just switches the quantifiers in the second conjunct of Crooked:

It is easy to model the rigged lottery using plausibility. Indeed, it is easy to check that the relational possibility structure M₁ satisfies Lottery ∧ Rigged. However, Rigged is not satisfiable in ^rank,fo₁ (Exercise 10.23). Intuitively, if M ∈ ^rank,fo₁ satisfies Rigged, consider the individual d such that [[Winner(d)]]_M is minimum. (Since ranks are natural numbers, there has to be such an individual d.) But Rigged says that there has to be an individual who is more likely to win than d; this quickly leads to a contradiction.

Examples 10.4.3, 10.4.4, and 10.4.5 show that AX^cond,fo_n (even with C5 and C6) is not a complete axiomatization for the language ^→,fo_n with respect to any of ^poss⁺,fo_n, ^rank,fo_n, ^rank,fo_n, or ^pref,fo_n: Lottery is valid in ^rank⁺,fo₁, but is not provable in AX^{cond, fo}₁ even with C5 and C6 (if it were, it would be valid in plausibility structures that satisfy C5 and C6, which Example 8.1.2 shows it is not); similarly, (Lottery ∧ Crooked) is valid in ^poss⁺,fo₁ and ^pref,fo₁ and is not provable in AX^{cond, fo}₁, and Rigged is valid in ^rank,fo₁ but is not provable in AX^cond,fo₁. These examples show that first-order conditional logic can distinguish these different representations of uncertainty although propositional conditional logic cannot.

Both the domain D_lot and the set w_lot of worlds in M_lot are infinite. This is not an accident. The formula Lottery is not satisfiable in any relational plausibility structure with either a finite domain or a finite set of worlds (or, more accurately, it is satisfiable in such a structure only if ⊥ = ⊺). This follows from the following more general result:

Proposition 10.4.6

Suppose that M = (W, D, 풫₁, …, 풫_n π) and either W or D is finite. If x does not appear free in ψ, then the following axiom is valid in M:

Proof See Exercise 10.24.

Corollary 10.4.7

Suppose that M = (W, D, 풫, π) and either W or D is finite. Then M ⊨ ∀x(true → Winner(x)) → true → ∀x Winner(x). Hence M ⊨ Lottery → (true → false).

Proof It is immediate from Proposition 10.4.6 that

Thus, if (M, w) ⊨ Lottery, then

From the AND rule (C2) and right weakening (RC2), it follows that

Thus, M ⊨ Lottery → (true → false).

Corollary 10.4.7 shows that if W or D is finite, then if each person is unlikely to win the lottery, then it is unlikely that anyone will win. To avoid this situation (at least in the framework of plausibility measures and thus in all the other representations that can be used to model default reasoning, which can all be viewed as instances of qualitative plausibility measures), an infinite domain and an infinite number of possible worlds are both required. The structure M_lot shows that Lottery ∧ (true → false) is satisfiable in a structure with an infinite domain and an infinite set of worlds. In fact, M_lot shows that ∀x(true → Winner(x) ∧ (true → ∀x Winner(x)) is satisfiable.

Recall that in Section 8.2 it was shown that the definition of B_iφ in terms of plausibility, as Pl([[φ]]) > Pl([[ φ]]) (or, equivalently, defining B_iφ as true → _i φ) is equivalent to the definition given in terms of a binary relation _i provided that the set of possible worlds is finite (cf. Exercise 8.7). The lottery paradox shows that they are not equivalent with infinitely many worlds. It is not hard to show that B_i defined in terms of a _i relation satisfies the property ∀xB_iφ → B_i∀xφ (Exercise 10.25). But under the identification of B_iφ with true → _i φ this is precisely C9, which does not hold in general.

C9 can be viewed as an instance of an infinitary AND rule since, roughly speaking, it says that if ψ → φ(d) holds for all d ∈ D, then ψ → ∧_d∈Dφ(d) holds. It was shown in Section 8.1 that Pl4 sufficed to give the (finitary) AND rule and that a natural generalization of Pl4, Pl4*, sufficed for the infinitary version. Pl4* does not hold for relational qualitative plausibility structures in general (in particular, as observed in Section 8.1, it does not hold for the structure M_lot from Example 10.4.3). However, it does hold in ^rank,fo_n.

Proposition 10.4.8

Pl4* holds in every structure in ^rank⁺,fo_n.

Proof See Exercise 10.26.

The following proposition shows that C9 follows from Pl4*:

Proposition 10.4.9

C9 is valid in all relational plausibility structures satisfying Pl4*.

Proof See Exercise 10.27.

Propositions 10.4.8 and 10.4.9 explain why the lottery paradox cannot be captured in ^poss⁺,fo_n. Neither Pl4* nor C9 hold in general in ^rank⁺,fo_n or ^pref,fo_n. Indeed, the structure M₂ described in Example 10.4.3 and its analogue in ^pref,fo₁ provide counterexamples (Exercise 10.28), which is why Lottery holds in these structures. So why is (Lottery ∧ Crooked) valid in ^poss⁺,fo₁ and ^pref,fo₁? The following two properties of plausibility help to explain why. The first is an infinitary version of Pl4 slightly weaker than Pl4*; the second is an infinitary version of Pl5.

Pl4^†. For any index set I such that 0 ∈ I and |I |≥ 2, if {U_i : i ∈ I} are pairwise disjoint sets, and Pl(U₀) > Pl(U_i) for all i ∈ I −{0}, then Pl(U₀) ≮ Pl (∪_{i∈I, i≠0}U_i).
Pl5*. For any index set I, if {U_i : i ∈ I} are sets such that Pl(U_i) =⊥ for i ∈ I, then Pl(∪_i∈I U_i) = ⊥.

It is easy to see that Pl4^† is implied by Pl4*. For suppose that Pl satisfies Pl4* and the preconditions of Pl4^†. Let U = ∪_i∈I U_i. By Pl3, Pl(U₀) > Pl(U_i) implies that Pl(U − U_i) > Pl(U_i). Since this is true for all i ∈ I, by Pl4*, Pl(U₀) > Pl(U − U₀). Therefore Pl(U₀) ≮ Pl(U − U₀), so Pl satisfies Pl4*. However, Pl4^† can hold in structures that do not satisfy Pl4*. In fact, the following proposition shows that Pl4^† holds in every structure in ^poss⁺,fo_n and ^pref,fo_n (including the ones that satisfy Lottery, and hence do not satisfy Pl4*):

Proposition 10.4.10

Pl4^† holds in every structure in ^pref,fo_n and ^poss⁺,fo_n.

Proof See Exercise 10.29.

Pl5* is an infinitary version of Pl5. It is easy to verify that it holds for ranking functions that satisfy Rk3⁺, possibility measures, and preferential structures.

Proposition 10.4.11

Pl5* holds in every relational plausibility structure in ^rank⁺,fo_n, ^poss⁺,fo_n and ^pref,fo_n.

Proof See Exercise 10.30.

Pl5* has elegant axiomatic consequences.

Proposition 10.4.12

The axiom

C10. ∀xN_iφ → N_i(∀xφ)

is sound in relational qualitative plausibility structures satisfying Pl5*; the axiom

C11. ∀x(φ(x) →_i ψ) → ((∃xφ(x)) →_i ψ), if x does not appear free in ψ,

is sound in structures satisfying Pl4^† and Pl5*.

Proof See Exercise 10.31.

Axiom C11 can be viewed as an infinitary version of the OR rule (C3), just as C9 can be viewed as an infinitary version of the AND rule (C2). Abusing notation yet again, the antecedent of C11 says that ∧_d∈D(φ(d) →_i ψ), while the conclusion says that (φ_d∈Dφ(d)) →_i ψ.

When Pl4^† and Pl5* hold, the crooked lottery is (almost) inconsistent.

Proposition 10.4.13

The formula Lottery ∧ Crooked → (true → false) is valid in structures satisfying Pl4^† and Pl5*.

Proof See Exercise 10.32.

Since Pl4^† and Pl5* are valid in ^poss⁺,fo_n, as is (true → false), it immediately follows that Lottery ∧ Crooked is unsatisfiable in ^poss⁺,fo_n.

To summarize, this discussion vindicates the intuition that there are significant differences between the various approaches used to give semantics to conditional logic, despite the fact that, at the propositional level, they are essentially equivalent. The propositional language is simply too weak to bring out the differences. Using plausibility makes it possible to delineate the key properties that distinguish the various approaches, properties such as Pl4*, Pl4^†, and Pl5*, which manifest themselves in axioms such as C9, C10, and C11.

Conditional logic was introduced in Section 8.6 as a tool for reasoning about defaults. Does the preceding analysis have anything to say about default reasoning? For that matter, how should defaults even be captured in first-order conditional logic? Statements like "birds typically fly" are similar in spirit to statements like "90 percent of birds fly." Using ∀x (Bird(x) → Flies(x)) to represent this formula is just as inappropriate as using ∀x(ℓ(Flies(x) | Bird(x)) > .9) to represent "90 percent of birds fly." The latter statement is perhaps best represented statistically, using a probability on the domain, not a probability on possible worlds. Similarly, it seems that "birds typically fly" should be represented using statistical plausibility. On the other hand, conclusions about individual birds (such as "Tweety is a bird, so Tweety (by default) flies") are similar in spirit to statements like "The probability that Tweety (a particular bird) flies is greater than .9"; these are best represented using plausibility on possible worlds.

Drawing the conclusion "Tweety flies" from "birds typically fly" would then require some way of connecting statistical plausibility with plausibility on possible worlds. There are no techniques given in this chapter for doing that; that is the subject of Chapter 11.