3.6 Conditioning Belief Functions

The appropriate way to condition a belief function depends on how it is interpreted. If it is viewed as a lower probability, then the ideas of Section 3.3 apply. On the other hand, if it is viewed as a way of measuring the evidence that supports an event, a different approach to conditioning is appropriate.

Recall from Theorem 2.4.1 that given a belief function Bel, the set _Bel = {μ : μ (U) ≥ Bel(U} for all U ⊆ W} of probability measures is such that Bel = (_Bel)_* and Plaus = (_Bel)* The association of Bel with _Bel can be used to define a notion of conditional belief in terms of conditioning on sets of probability measures.

Definition 3.6.1

Given a belief function Bel defined on W and a set U such that Plaus(U) > 0, define functions Bel|U : 2^W → [0, 1] and Plaus|U : 2^W → [0, 1] as follows:

Given the close relationship between beliefs and inner measures, the following analogue of Theorem 3.5.1 should not come as a great surprise.

Theorem 3.6.2

Suppose that Plaus(U) > 0. Then

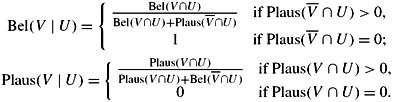
Proof See Exercise 3.15.

By definition, a conditional probability measure is a probability measure. If Bel|U is to be viewed as the result of conditioning the belief function Bel on V, an obvious question to ask is whether Bel|U is in fact a belief function. It is far from clear that it is. Recall that the lower probability of an arbitrary set of probability measures is not in general a belief function, since lower probabilities do not necessarily satisfy B3 (Exercise 2.14). Fortunately, as the next result shows, Bel|U is indeed a belief function, and Plaus|U is the corresponding plausibility function.

Theorem 3.6.3

Let Bel be a belief function on W and Plaus the corresponding plausibility function. Suppose that U ⊆ W and Plaus(U) > 0. Then Bel|U is a belief function and Plaus|U is the corresponding plausibility function.

Proof The proof that Plaus(V | U) = 1 − Bel(V | U) is straightforward and left to the reader (Exercise 3.16). Thus, provided that Bel|U is a belief function, then Plaus|U is the corresponding plausibility function. Clearly Bel|U satisfies B1 and B2. The proof that Bel|U satisfies B3 proceeds by induction on n; it is somewhat difficult and beyond the scope of this book.

This approach to defining conditional belief reduces a belief function Bel to a set of probability measures whose lower probability is Bel, namely _Bel. But, as observed in Chapter 2 (see Exercise 2.24), there are in general a number of sets of probability measures all of whose lower probabilities are Bel. While Theorem 3.6.2 holds for _Bel (i.e., taking Bel|U = (_Bel|U)*), it does not hold for an arbitrary set such that _* = Bel; that is, even if _* = Bel, it is not the case that (|U)_* = (_Bel|U)_*, so (|U)_* is not necessarily Bel|U (Exercise 3.17). This is a minor annoyance. Theorem 3.6.2 can be taken as the definition of Bel|U. This has the advantage of being a definition of Bel|U that is given completely in terms of Bel, not in terms of an associated set of probability measures. The fact that this definition agrees with conditioning on _Bel can then be taken as evidence of the reasonableness of this approach.

Another notion of conditioning belief functions, arguably more appropriate if a belief function is viewed as a way of representing the evidence supporting an event, can be defined using the Rule of Combination. In this approach, the information U is represented by the mass function m_U that gives U mass 1 and all other sets mass 0. Note that the belief function Bel_U based on m_U is such that Bel_U (V) = 1if U ⊆ V and Bel_U (V) = 0 otherwise.

Definition 3.6.4

Given a belief function Bel based on mass function m, let Bel||U be the belief function based on the mass function m ⊕ m_U.

Proposition 3.6.5

Bel||U is defined exactly if Plaus(U) > 0, in which case

The corresponding plausibility function Plaus||U is defined as

Proof See Exercise 3.18.

I typically write Bel(V || U) and Plaus(V || U) rather than Bel||U(V) and Plaus||U(V); I call this DS conditioning. Note that Plaus(V || U) looks just like probabilistic conditioning, using Plaus instead of μ. It is immediate from Proposition 3.6.5 that an analogue of Bayes' Rule holds for Plaus||U. There is no obvious analogue that holds in the case of Bel||U, Bel|U, or Plaus|U.

If Bel is in fact a probability measure (so that Bel(V) = Plaus(V) for all V ⊆ W), then Bel(V | U) = Bel(V || U); both definitions agree with the standard definition of conditional probability (Exercise 3.19). In general, however, Bel(V | U) and Bel(V || U) are different. However, it can be shown that [Bel(V || U), Plaus(V || U)] is a subinterval of [Bel(V | U), Plaus(V | U)].

Theorem 3.6.6

If Plaus(U) > 0, then

Proof Because Bel(V | U) = 1 − Plaus(V | U) and Bel(V || U) = 1 − Plaus(V || U), it suffices to prove that Plaus(V || U) ≤ Plaus(V | U). If Plaus(V ∩ U) = 0, then it is immediate from Theorem 3.6.2 and Proposition 3.6.5 that Plaus(V || U) = Plaus(V | U) = 0. If Plaus(V ∩ U) > 0, it clearly suffices to show that Plaus(U) ≥ Plaus(V ∩ U) + Bel(V ∩ U). This is left to the reader (Exercise 3.20).

As the following example shows, in general, [Bel(V || U), Plaus(V || U)] is a strict subinterval of [Bel(V | U), Plaus(V | U)]:

Example 3.6.7

Consider the result of applying the two definitions of conditional belief to analyzing the three-prisoners puzzle. Using the same notation as in Example 3.3.1, let m be the mass function that assigns probability 1/3 to each of the three disjoint sets lives -a, lives -b, and lives -c, and let Bel and Plaus be the belief function and plausibility functions respectively, corresponding to m. Using Proposition 3.6.5, it follows that Bel(lives -a || says-b) = Plaus(lives -a || says-b) = 1/2. Thus, for DS conditioning, the range reduces to the single point 1/2 (intuitively, the "wrong" answer). By way of contrast, it follows from Definition 3.6.1 and Example 3.3.1 that Bel(lives -a | says-b) = 0 while Plaus(lives -a | says-b) = 1/2.

Example 3.6.7 shows that DS conditioning can give counterintuitive answers. Intuitively, this is because the lower probability interpretation of belief functions seems more appropriate in this example. While Example 2.4.6 and results such as Theorems 3.4.5 and 3.4.6 show that Dempster's Rule of Combination can give quite reasonable results, an extra argument needs to be made regarding when it is appropriate to represent the evidence U by the belief function Bel_U. Such arguments have been made; see the notes to this chapter for more details and references. Nevertheless, these examples do point out the need to be exceedingly careful about the underlying interpretation of a belief function when trying to condition on new information.